Menu Close

Question-125444

Tinku Tara 0 Comments
Pin




Question Number 125444 by ajfour last updated on 11/Dec/20
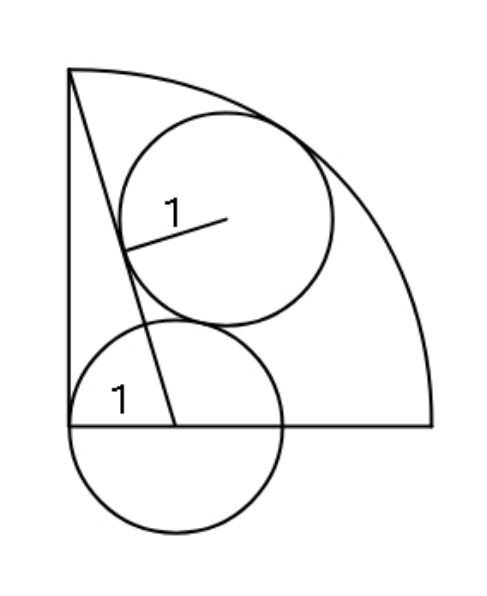
Commented by ajfour last updated on 11/Dec/20
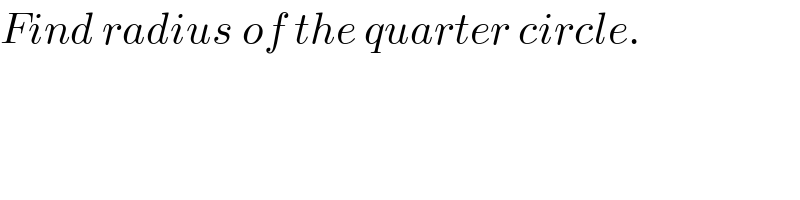
Find radius of the quarter circle.
$${Find}\:{radius}\:{of}\:{the}\:{quarter}\:{circle}. \\ $$
Answered by ajfour last updated on 11/Dec/20
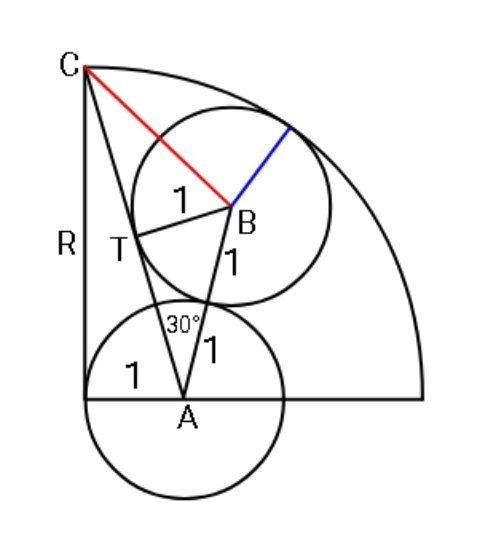
Commented by ajfour last updated on 11/Dec/20
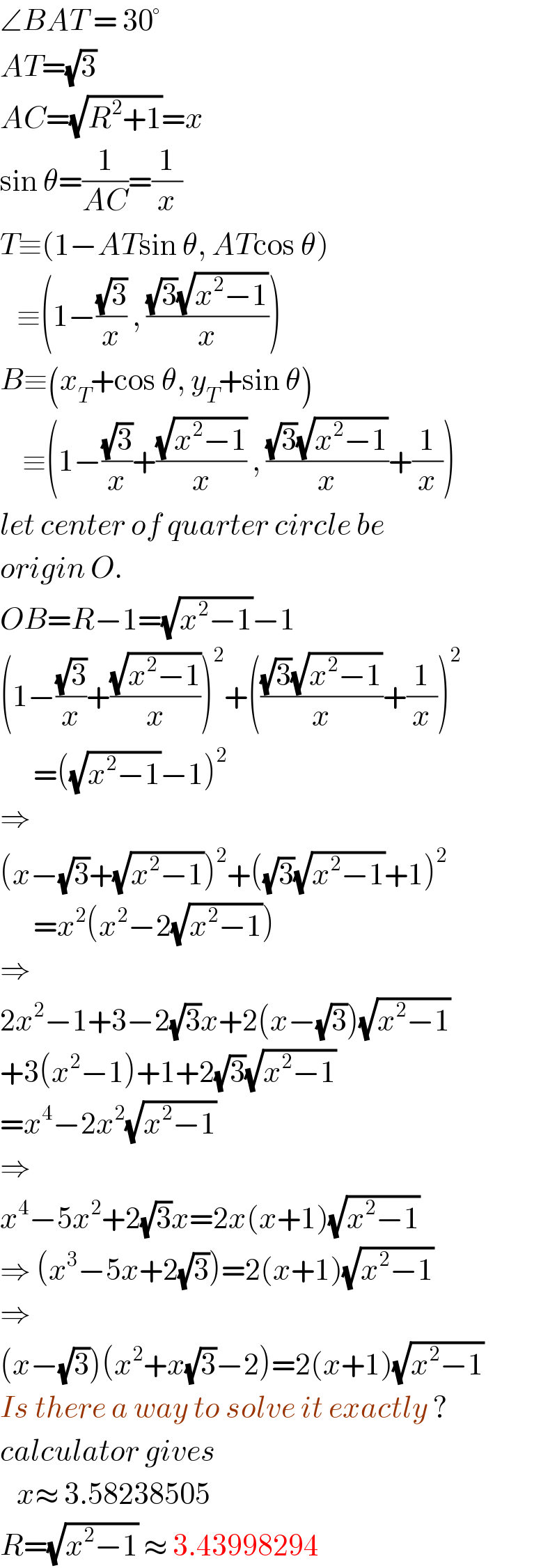
∠BAT = 30° AT=(√3) AC=(√(R^2 +1))=x sin θ=(1/(AC))=(1/x) T≡(1−ATsin θ, ATcos θ) ≡(1−((√3)/x) , (((√3)(√(x^2 −1)))/x)) B≡(x_T +cos θ, y_T +sin θ) ≡(1−((√3)/x)+((√(x^2 −1))/x) , (((√3)(√(x^2 −1)))/x)+(1/x)) let center of quarter circle be origin O. OB=R−1=(√(x^2 −1))−1 (1−((√3)/x)+((√(x^2 −1))/x))^2 +((((√3)(√(x^2 −1)))/x)+(1/x))^2 =((√(x^2 −1))−1)^2 ⇒ (x−(√3)+(√(x^2 −1)))^2 +((√3)(√(x^2 −1))+1)^2 =x^2 (x^2 −2(√(x^2 −1))) ⇒ 2x^2 −1+3−2(√3)x+2(x−(√3))(√(x^2 −1)) +3(x^2 −1)+1+2(√3)(√(x^2 −1)) =x^4 −2x^2 (√(x^2 −1)) ⇒ x^4 −5x^2 +2(√3)x=2x(x+1)(√(x^2 −1)) ⇒ (x^3 −5x+2(√3))=2(x+1)(√(x^2 −1)) ⇒ (x−(√3))(x^2 +x(√3)−2)=2(x+1)(√(x^2 −1)) Is there a way to solve it exactly ? calculator gives x≈ 3.58238505 R=(√(x^2 −1)) ≈ 3.43998294
$$\angle{BAT}\:=\:\mathrm{30}° \\ $$$${AT}=\sqrt{\mathrm{3}} \\ $$$${AC}=\sqrt{{R}^{\mathrm{2}} +\mathrm{1}}={x} \\ $$$$\mathrm{sin}\:\theta=\frac{\mathrm{1}}{{AC}}=\frac{\mathrm{1}}{{x}} \\ $$$${T}\equiv\left(\mathrm{1}−{AT}\mathrm{sin}\:\theta,\:{AT}\mathrm{cos}\:\theta\right) \\ $$$$\:\:\:\equiv\left(\mathrm{1}−\frac{\sqrt{\mathrm{3}}}{{x}}\:,\:\frac{\sqrt{\mathrm{3}}\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}}{{x}}\right) \\ $$$${B}\equiv\left({x}_{{T}} +\mathrm{cos}\:\theta,\:{y}_{{T}} +\mathrm{sin}\:\theta\right) \\ $$$$\:\:\:\:\equiv\left(\mathrm{1}−\frac{\sqrt{\mathrm{3}}}{{x}}+\frac{\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}}{{x}}\:,\:\frac{\sqrt{\mathrm{3}}\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}}{{x}}+\frac{\mathrm{1}}{{x}}\right) \\ $$$${let}\:{center}\:{of}\:{quarter}\:{circle}\:{be} \\ $$$${origin}\:{O}. \\ $$$${OB}={R}−\mathrm{1}=\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}−\mathrm{1} \\ $$$$\left(\mathrm{1}−\frac{\sqrt{\mathrm{3}}}{{x}}+\frac{\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}}{{x}}\right)^{\mathrm{2}} +\left(\frac{\sqrt{\mathrm{3}}\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}}{{x}}+\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:=\left(\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}−\mathrm{1}\right)^{\mathrm{2}} \\ $$$$\Rightarrow \\ $$$$\left({x}−\sqrt{\mathrm{3}}+\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}\right)^{\mathrm{2}} +\left(\sqrt{\mathrm{3}}\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}+\mathrm{1}\right)^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:={x}^{\mathrm{2}} \left({x}^{\mathrm{2}} −\mathrm{2}\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}\right) \\ $$$$\Rightarrow \\ $$$$\mathrm{2}{x}^{\mathrm{2}} −\mathrm{1}+\mathrm{3}−\mathrm{2}\sqrt{\mathrm{3}}{x}+\mathrm{2}\left({x}−\sqrt{\mathrm{3}}\right)\sqrt{{x}^{\mathrm{2}} −\mathrm{1}} \\ $$$$+\mathrm{3}\left({x}^{\mathrm{2}} −\mathrm{1}\right)+\mathrm{1}+\mathrm{2}\sqrt{\mathrm{3}}\sqrt{{x}^{\mathrm{2}} −\mathrm{1}} \\ $$$$={x}^{\mathrm{4}} −\mathrm{2}{x}^{\mathrm{2}} \sqrt{{x}^{\mathrm{2}} −\mathrm{1}} \\ $$$$\Rightarrow \\ $$$${x}^{\mathrm{4}} −\mathrm{5}{x}^{\mathrm{2}} +\mathrm{2}\sqrt{\mathrm{3}}{x}=\mathrm{2}{x}\left({x}+\mathrm{1}\right)\sqrt{{x}^{\mathrm{2}} −\mathrm{1}} \\ $$$$\Rightarrow\:\left({x}^{\mathrm{3}} −\mathrm{5}{x}+\mathrm{2}\sqrt{\mathrm{3}}\right)=\mathrm{2}\left({x}+\mathrm{1}\right)\sqrt{{x}^{\mathrm{2}} −\mathrm{1}} \\ $$$$\Rightarrow \\ $$$$\left({x}−\sqrt{\mathrm{3}}\right)\left({x}^{\mathrm{2}} +{x}\sqrt{\mathrm{3}}−\mathrm{2}\right)=\mathrm{2}\left({x}+\mathrm{1}\right)\sqrt{{x}^{\mathrm{2}} −\mathrm{1}} \\ $$$${Is}\:{there}\:{a}\:{way}\:{to}\:{solve}\:{it}\:{exactly}\:? \\ $$$${calculator}\:{gives} \\ $$$$\:\:\:{x}\approx\:\mathrm{3}.\mathrm{58238505} \\ $$$${R}=\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}\:\approx\:\mathrm{3}.\mathrm{43998294} \\ $$
Commented by ajfour last updated on 11/Dec/20

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *