Menu Close

Question-125450

Tinku Tara 0 Comments
Pin




Question Number 125450 by joki last updated on 11/Dec/20
Answered by Dwaipayan Shikari last updated on 11/Dec/20
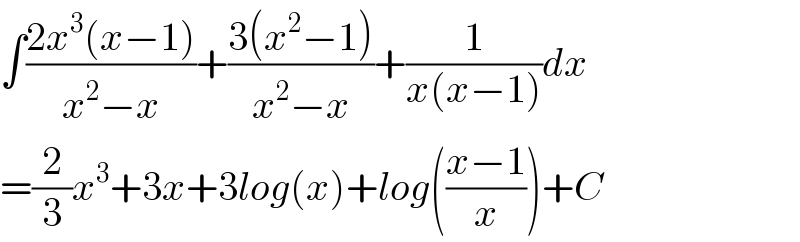
∫((2x^3 (x−1))/(x^2 −x))+((3(x^2 −1))/(x^2 −x))+(1/(x(x−1)))dx =(2/3)x^3 +3x+3log(x)+log(((x−1)/x))+C
$$\int\frac{\mathrm{2}{x}^{\mathrm{3}} \left({x}−\mathrm{1}\right)}{{x}^{\mathrm{2}} −{x}}+\frac{\mathrm{3}\left({x}^{\mathrm{2}} −\mathrm{1}\right)}{{x}^{\mathrm{2}} −{x}}+\frac{\mathrm{1}}{{x}\left({x}−\mathrm{1}\right)}{dx} \\ $$$$=\frac{\mathrm{2}}{\mathrm{3}}{x}^{\mathrm{3}} +\mathrm{3}{x}+\mathrm{3}{log}\left({x}\right)+{log}\left(\frac{{x}−\mathrm{1}}{{x}}\right)+{C} \\ $$
Commented by joki last updated on 11/Dec/20
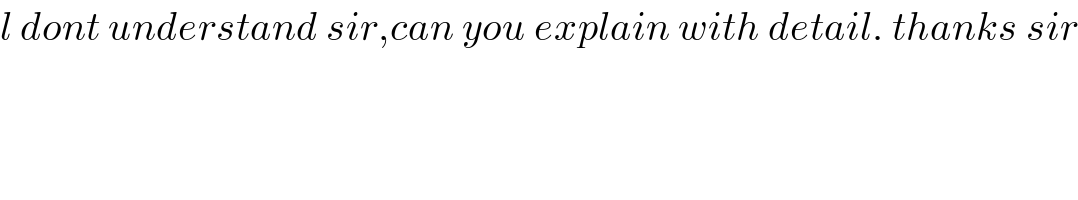
l dont understand sir,can you explain with detail. thanks sir
$${l}\:{dont}\:{understand}\:{sir},{can}\:{you}\:{explain}\:{with}\:{detail}.\:{thanks}\:{sir} \\ $$
Commented by Ar Brandon last updated on 11/Dec/20
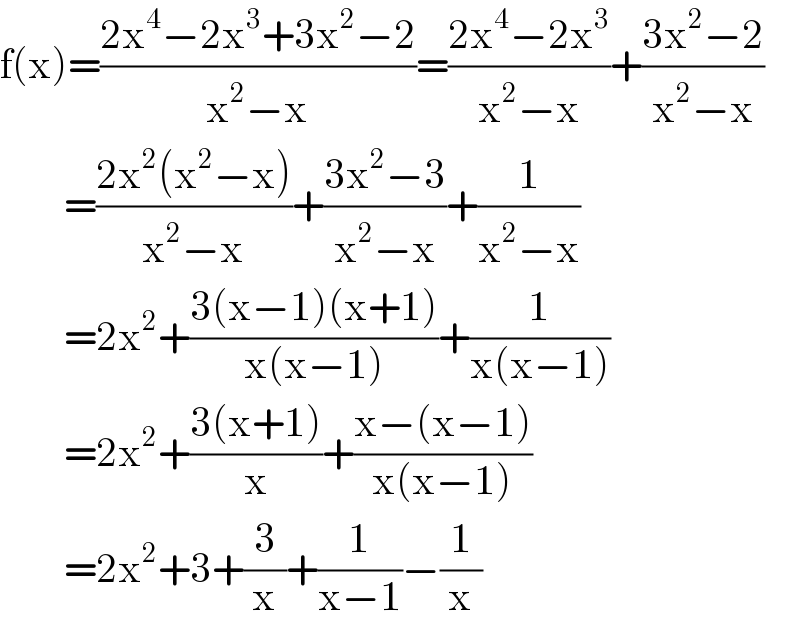
f(x)=((2x^4 −2x^3 +3x^2 −2)/(x^2 −x))=((2x^4 −2x^3 )/(x^2 −x))+((3x^2 −2)/(x^2 −x)) =((2x^2 (x^2 −x))/(x^2 −x))+((3x^2 −3)/(x^2 −x))+(1/(x^2 −x)) =2x^2 +((3(x−1)(x+1))/(x(x−1)))+(1/(x(x−1))) =2x^2 +((3(x+1))/x)+((x−(x−1))/(x(x−1))) =2x^2 +3+(3/x)+(1/(x−1))−(1/x)
$$\mathrm{f}\left(\mathrm{x}\right)=\frac{\mathrm{2x}^{\mathrm{4}} −\mathrm{2x}^{\mathrm{3}} +\mathrm{3x}^{\mathrm{2}} −\mathrm{2}}{\mathrm{x}^{\mathrm{2}} −\mathrm{x}}=\frac{\mathrm{2x}^{\mathrm{4}} −\mathrm{2x}^{\mathrm{3}} }{\mathrm{x}^{\mathrm{2}} −\mathrm{x}}+\frac{\mathrm{3x}^{\mathrm{2}} −\mathrm{2}}{\mathrm{x}^{\mathrm{2}} −\mathrm{x}} \\ $$$$\:\:\:\:\:\:\:\:=\frac{\mathrm{2x}^{\mathrm{2}} \left(\mathrm{x}^{\mathrm{2}} −\mathrm{x}\right)}{\mathrm{x}^{\mathrm{2}} −\mathrm{x}}+\frac{\mathrm{3x}^{\mathrm{2}} −\mathrm{3}}{\mathrm{x}^{\mathrm{2}} −\mathrm{x}}+\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} −\mathrm{x}} \\ $$$$\:\:\:\:\:\:\:\:=\mathrm{2x}^{\mathrm{2}} +\frac{\mathrm{3}\left(\mathrm{x}−\mathrm{1}\right)\left(\mathrm{x}+\mathrm{1}\right)}{\mathrm{x}\left(\mathrm{x}−\mathrm{1}\right)}+\frac{\mathrm{1}}{\mathrm{x}\left(\mathrm{x}−\mathrm{1}\right)} \\ $$$$\:\:\:\:\:\:\:\:=\mathrm{2x}^{\mathrm{2}} +\frac{\mathrm{3}\left(\mathrm{x}+\mathrm{1}\right)}{\mathrm{x}}+\frac{\mathrm{x}−\left(\mathrm{x}−\mathrm{1}\right)}{\mathrm{x}\left(\mathrm{x}−\mathrm{1}\right)} \\ $$$$\:\:\:\:\:\:\:\:=\mathrm{2x}^{\mathrm{2}} +\mathrm{3}+\frac{\mathrm{3}}{\mathrm{x}}+\frac{\mathrm{1}}{\mathrm{x}−\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{x}} \\ $$
Answered by john_santu last updated on 11/Dec/20
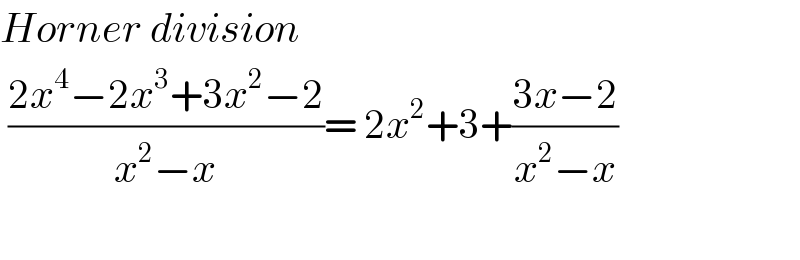
Horner division ((2x^4 −2x^3 +3x^2 −2)/(x^2 −x))= 2x^2 +3+((3x−2)/(x^2 −x))
$${Horner}\:{division} \\ $$$$\:\frac{\mathrm{2}{x}^{\mathrm{4}} −\mathrm{2}{x}^{\mathrm{3}} +\mathrm{3}{x}^{\mathrm{2}} −\mathrm{2}}{{x}^{\mathrm{2}} −{x}}=\:\mathrm{2}{x}^{\mathrm{2}} +\mathrm{3}+\frac{\mathrm{3}{x}−\mathrm{2}}{{x}^{\mathrm{2}} −{x}} \\ $$$$ \\ $$
Answered by mathmax by abdo last updated on 11/Dec/20
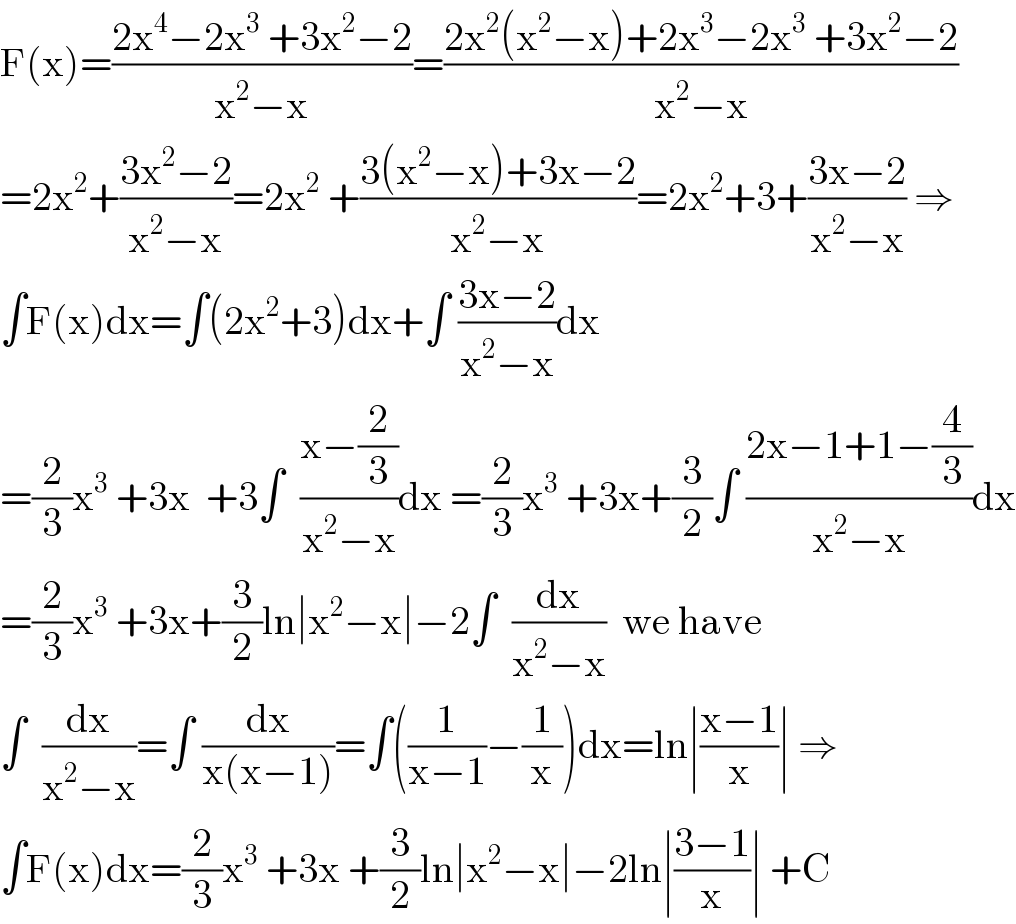
F(x)=((2x^4 −2x^3 +3x^2 −2)/(x^2 −x))=((2x^2 (x^2 −x)+2x^3 −2x^3 +3x^2 −2)/(x^2 −x)) =2x^2 +((3x^2 −2)/(x^2 −x))=2x^2 +((3(x^2 −x)+3x−2)/(x^2 −x))=2x^2 +3+((3x−2)/(x^2 −x)) ⇒ ∫F(x)dx=∫(2x^2 +3)dx+∫ ((3x−2)/(x^2 −x))dx =(2/3)x^3 +3x +3∫ ((x−(2/3))/(x^2 −x))dx =(2/3)x^3 +3x+(3/2)∫ ((2x−1+1−(4/3))/(x^2 −x))dx =(2/3)x^3 +3x+(3/2)ln∣x^2 −x∣−2∫ (dx/(x^2 −x)) we have ∫ (dx/(x^2 −x))=∫ (dx/(x(x−1)))=∫((1/(x−1))−(1/x))dx=ln∣((x−1)/x)∣ ⇒ ∫F(x)dx=(2/3)x^3 +3x +(3/2)ln∣x^2 −x∣−2ln∣((3−1)/x)∣ +C
$$\mathrm{F}\left(\mathrm{x}\right)=\frac{\mathrm{2x}^{\mathrm{4}} −\mathrm{2x}^{\mathrm{3}} \:+\mathrm{3x}^{\mathrm{2}} −\mathrm{2}}{\mathrm{x}^{\mathrm{2}} −\mathrm{x}}=\frac{\mathrm{2x}^{\mathrm{2}} \left(\mathrm{x}^{\mathrm{2}} −\mathrm{x}\right)+\mathrm{2x}^{\mathrm{3}} −\mathrm{2x}^{\mathrm{3}} \:+\mathrm{3x}^{\mathrm{2}} −\mathrm{2}}{\mathrm{x}^{\mathrm{2}} −\mathrm{x}} \\ $$$$=\mathrm{2x}^{\mathrm{2}} +\frac{\mathrm{3x}^{\mathrm{2}} −\mathrm{2}}{\mathrm{x}^{\mathrm{2}} −\mathrm{x}}=\mathrm{2x}^{\mathrm{2}} \:+\frac{\mathrm{3}\left(\mathrm{x}^{\mathrm{2}} −\mathrm{x}\right)+\mathrm{3x}−\mathrm{2}}{\mathrm{x}^{\mathrm{2}} −\mathrm{x}}=\mathrm{2x}^{\mathrm{2}} +\mathrm{3}+\frac{\mathrm{3x}−\mathrm{2}}{\mathrm{x}^{\mathrm{2}} −\mathrm{x}}\:\Rightarrow \\ $$$$\int\mathrm{F}\left(\mathrm{x}\right)\mathrm{dx}=\int\left(\mathrm{2x}^{\mathrm{2}} +\mathrm{3}\right)\mathrm{dx}+\int\:\frac{\mathrm{3x}−\mathrm{2}}{\mathrm{x}^{\mathrm{2}} −\mathrm{x}}\mathrm{dx} \\ $$$$=\frac{\mathrm{2}}{\mathrm{3}}\mathrm{x}^{\mathrm{3}} \:+\mathrm{3x}\:\:+\mathrm{3}\int\:\:\frac{\mathrm{x}−\frac{\mathrm{2}}{\mathrm{3}}}{\mathrm{x}^{\mathrm{2}} −\mathrm{x}}\mathrm{dx}\:=\frac{\mathrm{2}}{\mathrm{3}}\mathrm{x}^{\mathrm{3}} \:+\mathrm{3x}+\frac{\mathrm{3}}{\mathrm{2}}\int\:\frac{\mathrm{2x}−\mathrm{1}+\mathrm{1}−\frac{\mathrm{4}}{\mathrm{3}}}{\mathrm{x}^{\mathrm{2}} −\mathrm{x}}\mathrm{dx} \\ $$$$=\frac{\mathrm{2}}{\mathrm{3}}\mathrm{x}^{\mathrm{3}} \:+\mathrm{3x}+\frac{\mathrm{3}}{\mathrm{2}}\mathrm{ln}\mid\mathrm{x}^{\mathrm{2}} −\mathrm{x}\mid−\mathrm{2}\int\:\:\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{2}} −\mathrm{x}}\:\:\mathrm{we}\:\mathrm{have} \\ $$$$\int\:\:\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{2}} −\mathrm{x}}=\int\:\frac{\mathrm{dx}}{\mathrm{x}\left(\mathrm{x}−\mathrm{1}\right)}=\int\left(\frac{\mathrm{1}}{\mathrm{x}−\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{x}}\right)\mathrm{dx}=\mathrm{ln}\mid\frac{\mathrm{x}−\mathrm{1}}{\mathrm{x}}\mid\:\Rightarrow \\ $$$$\int\mathrm{F}\left(\mathrm{x}\right)\mathrm{dx}=\frac{\mathrm{2}}{\mathrm{3}}\mathrm{x}^{\mathrm{3}} \:+\mathrm{3x}\:+\frac{\mathrm{3}}{\mathrm{2}}\mathrm{ln}\mid\mathrm{x}^{\mathrm{2}} −\mathrm{x}\mid−\mathrm{2ln}\mid\frac{\mathrm{3}−\mathrm{1}}{\mathrm{x}}\mid\:+\mathrm{C} \\ $$
Commented by mathmax by abdo last updated on 11/Dec/20
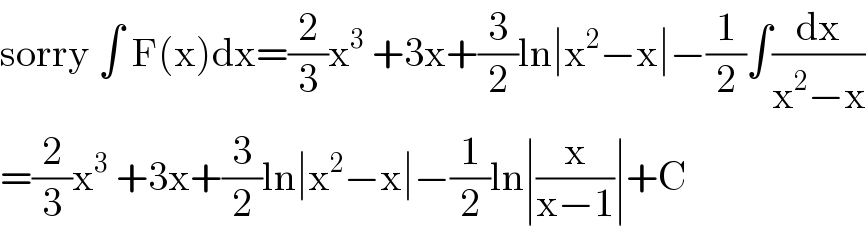
sorry ∫ F(x)dx=(2/3)x^3 +3x+(3/2)ln∣x^2 −x∣−(1/2)∫(dx/(x^2 −x)) =(2/3)x^3 +3x+(3/2)ln∣x^2 −x∣−(1/2)ln∣(x/(x−1))∣+C
$$\mathrm{sorry}\:\int\:\mathrm{F}\left(\mathrm{x}\right)\mathrm{dx}=\frac{\mathrm{2}}{\mathrm{3}}\mathrm{x}^{\mathrm{3}} \:+\mathrm{3x}+\frac{\mathrm{3}}{\mathrm{2}}\mathrm{ln}\mid\mathrm{x}^{\mathrm{2}} −\mathrm{x}\mid−\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{2}} −\mathrm{x}} \\ $$$$=\frac{\mathrm{2}}{\mathrm{3}}\mathrm{x}^{\mathrm{3}} \:+\mathrm{3x}+\frac{\mathrm{3}}{\mathrm{2}}\mathrm{ln}\mid\mathrm{x}^{\mathrm{2}} −\mathrm{x}\mid−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\mid\frac{\mathrm{x}}{\mathrm{x}−\mathrm{1}}\mid+\mathrm{C} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *