Question Number 125482 by joki last updated on 11/Dec/20

Answered by MJS_new last updated on 11/Dec/20
![∫((4x^3 +x^2 +1)/((x^2 −2)^3 ))dx= [Ostrogradski′s Method] =((x^3 −64x^2 −14x+64)/(32(x^2 −2)^2 ))+(1/(32))∫(dx/(x^2 −2))= =((x^3 −64x^2 −14x+64)/(32(x^2 −2)^2 ))+((√2)/(128))ln ∣(((√2)x−2)/( (√2)x+2))∣ +C](https://www.tinkutara.com/question/Q125494.png)
$$\int\frac{\mathrm{4}{x}^{\mathrm{3}} +{x}^{\mathrm{2}} +\mathrm{1}}{\left({x}^{\mathrm{2}} −\mathrm{2}\right)^{\mathrm{3}} }{dx}= \\ $$$$\:\:\:\:\:\left[\mathrm{Ostrogradski}'\mathrm{s}\:\mathrm{Method}\right] \\ $$$$=\frac{{x}^{\mathrm{3}} −\mathrm{64}{x}^{\mathrm{2}} −\mathrm{14}{x}+\mathrm{64}}{\mathrm{32}\left({x}^{\mathrm{2}} −\mathrm{2}\right)^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{32}}\int\frac{{dx}}{{x}^{\mathrm{2}} −\mathrm{2}}= \\ $$$$=\frac{{x}^{\mathrm{3}} −\mathrm{64}{x}^{\mathrm{2}} −\mathrm{14}{x}+\mathrm{64}}{\mathrm{32}\left({x}^{\mathrm{2}} −\mathrm{2}\right)^{\mathrm{2}} }+\frac{\sqrt{\mathrm{2}}}{\mathrm{128}}\mathrm{ln}\:\mid\frac{\sqrt{\mathrm{2}}{x}−\mathrm{2}}{\:\sqrt{\mathrm{2}}{x}+\mathrm{2}}\mid\:+{C} \\ $$
Commented by MJS_new last updated on 11/Dec/20

$$\mathrm{please}\:\mathrm{search}\:\mathrm{for}\:\mathrm{Ostrogradski}'\mathrm{s}\:\mathrm{Method} \\ $$$$\mathrm{here}\:\mathrm{or}\:\mathrm{on}\:\mathrm{the}\:\mathrm{www}.\:\mathrm{it}'\mathrm{s}\:\mathrm{easy}\:\mathrm{to}\:\mathrm{understand}. \\ $$$$\mathrm{I}\:\mathrm{don}'\mathrm{t}\:\mathrm{have}\:\mathrm{the}\:\mathrm{time}\:\mathrm{now}\:\mathrm{to}\:\mathrm{explain}\:\mathrm{it}\:\mathrm{again} \\ $$
Commented by joki last updated on 11/Dec/20
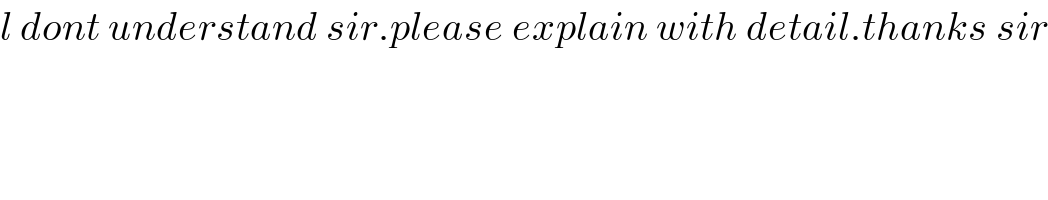
$${l}\:{dont}\:{understand}\:{sir}.{please}\:{explain}\:{with}\:{detail}.{thanks}\:{sir} \\ $$
Commented by MJS_new last updated on 14/Dec/20
![∫((P(x))/(Q(x)))dx=((P_1 (x))/(Q_1 (x)))+∫((P_2 (x))/(Q_2 (x)))dx where P(x), Q(x) are polynomes and the degree of P(x) < the degree of Q(x) and the fraction cannot be further simplified. then Q_1 (x)=gcd (Q(x), Q^′ (x)) and Q_2 (x)=((Q(x))/(Q_1 (x))) P_1 (x) and P_2 (x) are polynomes with degrees smaller than degrees of Q_1 (x) resp. Q_2 (x) we find the constants of P_1 (x), P_2 (x) by comparing the constants of both sides of ((P(x))/(Q(x)))=(d/dx)[((P_1 (x))/(Q_1 (x)))]+((P_2 (x))/(Q_2 (x)))](https://www.tinkutara.com/question/Q125878.png)
$$\int\frac{{P}\left({x}\right)}{{Q}\left({x}\right)}{dx}=\frac{{P}_{\mathrm{1}} \left({x}\right)}{{Q}_{\mathrm{1}} \left({x}\right)}+\int\frac{{P}_{\mathrm{2}} \left({x}\right)}{{Q}_{\mathrm{2}} \left({x}\right)}{dx} \\ $$$$\mathrm{where}\:{P}\left({x}\right),\:{Q}\left({x}\right)\:\mathrm{are}\:\mathrm{polynomes}\:\mathrm{and}\:\mathrm{the} \\ $$$$\mathrm{degree}\:\mathrm{of}\:{P}\left({x}\right)\:<\:\mathrm{the}\:\mathrm{degree}\:\mathrm{of}\:{Q}\left({x}\right)\:\mathrm{and}\:\mathrm{the} \\ $$$$\mathrm{fraction}\:\mathrm{cannot}\:\mathrm{be}\:\mathrm{further}\:\mathrm{simplified}. \\ $$$$\mathrm{then}\:{Q}_{\mathrm{1}} \left({x}\right)=\mathrm{gcd}\:\left({Q}\left({x}\right),\:{Q}^{'} \left({x}\right)\right) \\ $$$$\mathrm{and}\:{Q}_{\mathrm{2}} \left({x}\right)=\frac{{Q}\left({x}\right)}{{Q}_{\mathrm{1}} \left({x}\right)} \\ $$$${P}_{\mathrm{1}} \left({x}\right)\:\mathrm{and}\:{P}_{\mathrm{2}} \left({x}\right)\:\mathrm{are}\:\mathrm{polynomes}\:\mathrm{with}\:\mathrm{degrees} \\ $$$$\mathrm{smaller}\:\mathrm{than}\:\mathrm{degrees}\:\mathrm{of}\:{Q}_{\mathrm{1}} \left({x}\right)\:\mathrm{resp}.\:{Q}_{\mathrm{2}} \left({x}\right) \\ $$$$\mathrm{we}\:\mathrm{find}\:\mathrm{the}\:\mathrm{constants}\:\mathrm{of}\:{P}_{\mathrm{1}} \left({x}\right),\:{P}_{\mathrm{2}} \left({x}\right)\:\mathrm{by} \\ $$$$\mathrm{comparing}\:\mathrm{the}\:\mathrm{constants}\:\mathrm{of}\:\mathrm{both}\:\mathrm{sides}\:\mathrm{of} \\ $$$$\frac{{P}\left({x}\right)}{{Q}\left({x}\right)}=\frac{{d}}{{dx}}\left[\frac{{P}_{\mathrm{1}} \left({x}\right)}{{Q}_{\mathrm{1}} \left({x}\right)}\right]+\frac{{P}_{\mathrm{2}} \left({x}\right)}{{Q}_{\mathrm{2}} \left({x}\right)} \\ $$
Commented by joki last updated on 14/Dec/20

$$\mathrm{can}\:\mathrm{you}\:\mathrm{give}\:\mathrm{me}\:\mathrm{formula}\:\mathrm{your}\:\mathrm{answer}\:\mathrm{sir}\:?\mathrm{thanks}\:\mathrm{sir} \\ $$
Commented by joki last updated on 15/Dec/20
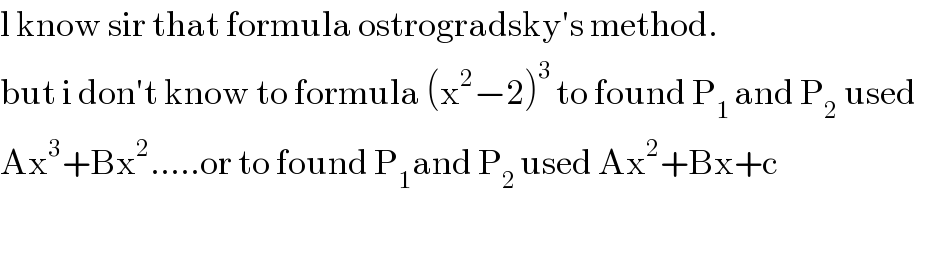
$$\mathrm{l}\:\mathrm{know}\:\mathrm{sir}\:\mathrm{that}\:\mathrm{formula}\:\mathrm{ostrogradsky}'\mathrm{s}\:\mathrm{method}. \\ $$$$\mathrm{but}\:\mathrm{i}\:\mathrm{don}'\mathrm{t}\:\mathrm{know}\:\mathrm{to}\:\mathrm{formula}\:\left(\mathrm{x}^{\mathrm{2}} −\mathrm{2}\right)^{\mathrm{3}\:} \mathrm{to}\:\mathrm{found}\:\mathrm{P}_{\mathrm{1}\:} \mathrm{and}\:\mathrm{P}_{\mathrm{2}} \:\mathrm{used}\:\: \\ $$$$\mathrm{Ax}^{\mathrm{3}} +\mathrm{Bx}^{\mathrm{2}} …..\mathrm{or}\:\mathrm{to}\:\mathrm{found}\:\mathrm{P}_{\mathrm{1}} \mathrm{and}\:\mathrm{P}_{\mathrm{2}\:} \mathrm{used}\:\mathrm{Ax}^{\mathrm{2}} +\mathrm{Bx}+\mathrm{c} \\ $$$$ \\ $$
Commented by Tawa11 last updated on 06/Nov/21

$$\mathrm{Great} \\ $$
