Question-125539

Question Number 125539 by ajfour last updated on 11/Dec/20

Commented by ajfour last updated on 11/Dec/20

The blue cubic curve is y=x^3 −21x−20 Find p.

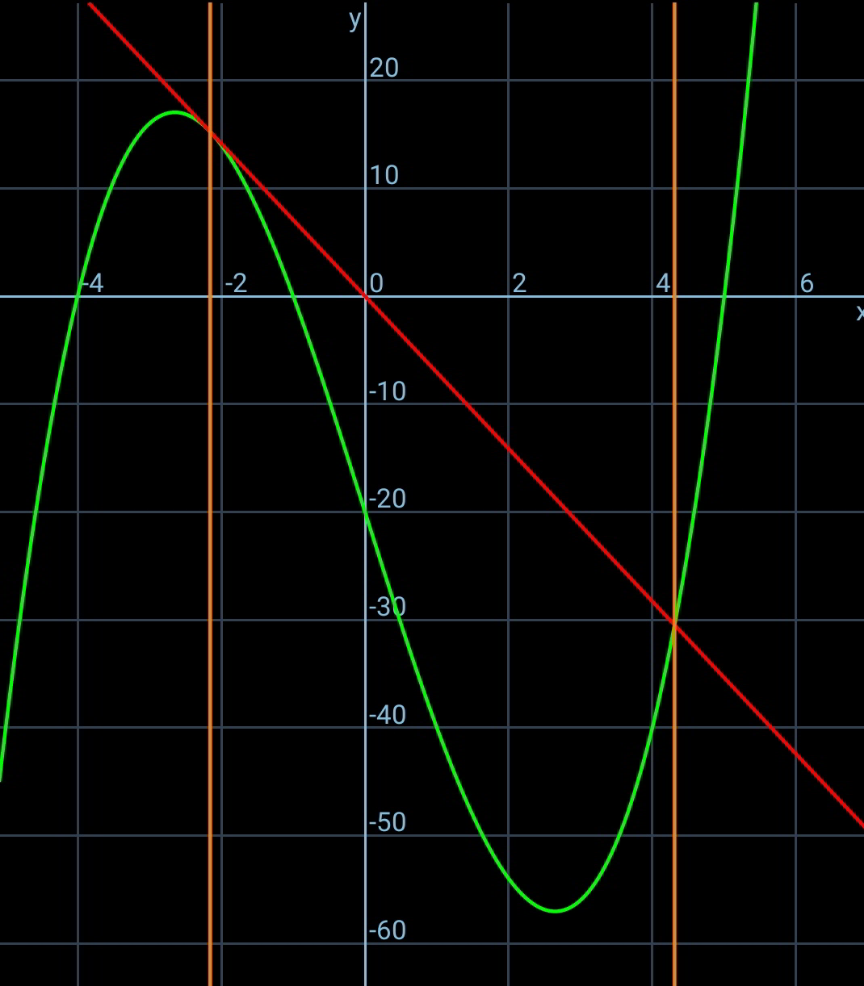
$${The}\:{blue}\:{cubic}\:{curve}\:{is} \\ $$$$\:\:{y}={x}^{\mathrm{3}} −\mathrm{21}{x}−\mathrm{20} \\ $$$${Find}\:{p}. \\ $$

Answered by mr W last updated on 12/Dec/20

y=x^3 −21x−20 red tangent line: y=3mx, say x^3 −21x−20=3mx x^3 −3(7+m)x−20=(x+q)^2 (x−p) =x^3 +(2q−p)x^2 +(q−2p)qx−pq^2 2q−p=0 (q−2p)q=−3(7+m) pq^2 =20 ⇒p=2q ⇒2q^3 =20 ⇒q=((10))^(1/3) ⇒p=2((10))^(1/3) ⇒−3(m+7)=((10))^(1/3) (−3((10))^(1/3) ) ⇒m=((100))^(1/3) −7

$${y}={x}^{\mathrm{3}} −\mathrm{21}{x}−\mathrm{20} \\ $$$${red}\:{tangent}\:{line}:\:{y}=\mathrm{3}{mx},\:{say} \\ $$$${x}^{\mathrm{3}} −\mathrm{21}{x}−\mathrm{20}=\mathrm{3}{mx} \\ $$$${x}^{\mathrm{3}} −\mathrm{3}\left(\mathrm{7}+{m}\right){x}−\mathrm{20}=\left({x}+{q}\right)^{\mathrm{2}} \left({x}−{p}\right) \\ $$$$={x}^{\mathrm{3}} +\left(\mathrm{2}{q}−{p}\right){x}^{\mathrm{2}} +\left({q}−\mathrm{2}{p}\right){qx}−{pq}^{\mathrm{2}} \\ $$$$ \\ $$$$\mathrm{2}{q}−{p}=\mathrm{0} \\ $$$$\left({q}−\mathrm{2}{p}\right){q}=−\mathrm{3}\left(\mathrm{7}+{m}\right) \\ $$$${pq}^{\mathrm{2}} =\mathrm{20} \\ $$$$ \\ $$$$\Rightarrow{p}=\mathrm{2}{q} \\ $$$$\Rightarrow\mathrm{2}{q}^{\mathrm{3}} =\mathrm{20} \\ $$$$\Rightarrow{q}=\sqrt[{\mathrm{3}}]{\mathrm{10}} \\ $$$$\Rightarrow{p}=\mathrm{2}\sqrt[{\mathrm{3}}]{\mathrm{10}} \\ $$$$\Rightarrow−\mathrm{3}\left({m}+\mathrm{7}\right)=\sqrt[{\mathrm{3}}]{\mathrm{10}}\left(−\mathrm{3}\sqrt[{\mathrm{3}}]{\mathrm{10}}\right) \\ $$$$\Rightarrow{m}=\sqrt[{\mathrm{3}}]{\mathrm{100}}−\mathrm{7} \\ $$

Commented by mr W last updated on 12/Dec/20

Commented by ajfour last updated on 12/Dec/20

Thanks Sir.

Answered by ajfour last updated on 12/Dec/20

y=x^3 −21x−20 y=mx say red line is tangent to curve at x=s ⇒ m=3s^2 −21 Intersections x^3 −(21+m)x−20=0 x^3 −(21+3s^2 −21)x−20=0 x^3 −3s^2 x−20=0 p+2s=0 ⇒ s=−(p/2) s^2 p=20 ⇒ p^3 =80 ________________________ p =2(10)^(1/3) ________________________

$${y}={x}^{\mathrm{3}} −\mathrm{21}{x}−\mathrm{20} \\ $$$${y}={mx} \\ $$$${say}\:{red}\:{line}\:{is}\:{tangent}\:{to}\:{curve} \\ $$$${at}\:{x}={s}\:\Rightarrow \\ $$$${m}=\mathrm{3}{s}^{\mathrm{2}} −\mathrm{21} \\ $$$${Intersections} \\ $$$${x}^{\mathrm{3}} −\left(\mathrm{21}+{m}\right){x}−\mathrm{20}=\mathrm{0} \\ $$$${x}^{\mathrm{3}} −\left(\mathrm{21}+\mathrm{3}{s}^{\mathrm{2}} −\mathrm{21}\right){x}−\mathrm{20}=\mathrm{0} \\ $$$${x}^{\mathrm{3}} −\mathrm{3}{s}^{\mathrm{2}} {x}−\mathrm{20}=\mathrm{0} \\ $$$${p}+\mathrm{2}{s}=\mathrm{0}\:\:\:\Rightarrow\:\:{s}=−\frac{{p}}{\mathrm{2}} \\ $$$${s}^{\mathrm{2}} {p}=\mathrm{20} \\ $$$$\Rightarrow\:\:{p}^{\mathrm{3}} =\mathrm{80} \\ $$$$\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_ \\ $$$$\:\:\:\:\:\:\:\:{p}\:\:=\mathrm{2}\left(\mathrm{10}\right)^{\mathrm{1}/\mathrm{3}} \\ $$$$\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_ \\ $$$$ \\ $$

Commented by ajfour last updated on 12/Dec/20

m=3s^2 −21 = 3((p^2 /4)−7) m = 3[(100)^(1/3) −7]

$${m}=\mathrm{3}{s}^{\mathrm{2}} −\mathrm{21}\:=\:\mathrm{3}\left(\frac{{p}^{\mathrm{2}} }{\mathrm{4}}−\mathrm{7}\right) \\ $$$$\:\:{m}\:=\:\mathrm{3}\left[\left(\mathrm{100}\right)^{\mathrm{1}/\mathrm{3}} −\mathrm{7}\right] \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply