Menu Close

Question-125572

Tinku Tara 0 Comments
Pin




Question Number 125572 by ajfour last updated on 12/Dec/20
Commented by ajfour last updated on 12/Dec/20
If equilateral triangle ABC has side length s=3 units, find x_A . Parabola eq. is y=x^2 .
$${If}\:{equilateral}\:{triangle}\:{ABC}\:{has} \\ $$$${side}\:{length}\:{s}=\mathrm{3}\:{units},\:{find}\:{x}_{{A}} . \\ $$$${Parabola}\:{eq}.\:{is}\:\:{y}={x}^{\mathrm{2}} . \\ $$
Commented by mr W last updated on 12/Dec/20
nice question again! i can not find an exact solution.
$${nice}\:{question}\:{again}! \\ $$$${i}\:{can}\:{not}\:{find}\:{an}\:{exact}\:{solution}. \\ $$
Answered by mr W last updated on 12/Dec/20
A(a,0) with a≥0 D(h,k) with D=midpoint BC k^2 +(h−a)^2 =((3s^2 )/4) ...(i) eqn. of BC: y=k−((h−a)/k)(x−h)=((a−h)/k)x+k−((h(a−h))/k) intersection x^2 =((a−h)/k)x+k−((h(a−h))/k) x^2 −((a−h)/k)x−k+((h(a−h))/k)=0 x_1 +x_2 =((a−h)/k)=2h ...(ii) x_1 x_2 =−k+((h(a−h))/k) (y_2 −y_1 )^2 +(x_2 −x_1 )^2 =s^2 (x_2 ^2 −x_1 ^2 )^2 +(x_2 −x_1 )^2 =s^2 [(x_2 +x_1 )^2 +1][(x_2 +x_1 )^2 −4x_1 x_2 ]=s^2 4(4h^2 +1)(h^2 +k−((h(a−h))/k))=s^2 ...(iii) from (ii): k=((a−h)/(2h)) ...(I) put (I) into (i): (((a−h)^2 )/(4h^2 ))+(a−h)^2 =((3s^2 )/4) (1+4h^2 )(a−h)^2 =3s^2 h^2 ⇒a=h(1+s(√(3/(1+4h^2 )))) ...(II) put into (iii): ⇒2(1+4h^2 )(s(√(3/(1+4h^2 )))−2h^2 )=s^2 ...(III) for a given s (≤4.73565) we get h from (III) and then a from (II).
$${A}\left({a},\mathrm{0}\right)\:{with}\:{a}\geqslant\mathrm{0} \\ $$$${D}\left({h},{k}\right)\:{with}\:{D}={midpoint}\:{BC} \\ $$$${k}^{\mathrm{2}} +\left({h}−{a}\right)^{\mathrm{2}} =\frac{\mathrm{3}{s}^{\mathrm{2}} }{\mathrm{4}}\:\:\:…\left({i}\right) \\ $$$${eqn}.\:{of}\:{BC}: \\ $$$${y}={k}−\frac{{h}−{a}}{{k}}\left({x}−{h}\right)=\frac{{a}−{h}}{{k}}{x}+{k}−\frac{{h}\left({a}−{h}\right)}{{k}} \\ $$$${intersection} \\ $$$${x}^{\mathrm{2}} =\frac{{a}−{h}}{{k}}{x}+{k}−\frac{{h}\left({a}−{h}\right)}{{k}} \\ $$$${x}^{\mathrm{2}} −\frac{{a}−{h}}{{k}}{x}−{k}+\frac{{h}\left({a}−{h}\right)}{{k}}=\mathrm{0} \\ $$$${x}_{\mathrm{1}} +{x}_{\mathrm{2}} =\frac{{a}−{h}}{{k}}=\mathrm{2}{h}\:\:\:…\left({ii}\right) \\ $$$${x}_{\mathrm{1}} {x}_{\mathrm{2}} =−{k}+\frac{{h}\left({a}−{h}\right)}{{k}} \\ $$$$\left({y}_{\mathrm{2}} −{y}_{\mathrm{1}} \right)^{\mathrm{2}} +\left({x}_{\mathrm{2}} −{x}_{\mathrm{1}} \right)^{\mathrm{2}} ={s}^{\mathrm{2}} \\ $$$$\left({x}_{\mathrm{2}} ^{\mathrm{2}} −{x}_{\mathrm{1}} ^{\mathrm{2}} \right)^{\mathrm{2}} +\left({x}_{\mathrm{2}} −{x}_{\mathrm{1}} \right)^{\mathrm{2}} ={s}^{\mathrm{2}} \\ $$$$\left[\left({x}_{\mathrm{2}} +{x}_{\mathrm{1}} \right)^{\mathrm{2}} +\mathrm{1}\right]\left[\left({x}_{\mathrm{2}} +{x}_{\mathrm{1}} \right)^{\mathrm{2}} −\mathrm{4}{x}_{\mathrm{1}} {x}_{\mathrm{2}} \right]={s}^{\mathrm{2}} \\ $$$$\mathrm{4}\left(\mathrm{4}{h}^{\mathrm{2}} +\mathrm{1}\right)\left({h}^{\mathrm{2}} +{k}−\frac{{h}\left({a}−{h}\right)}{{k}}\right)={s}^{\mathrm{2}} \:\:\:…\left({iii}\right) \\ $$$${from}\:\left({ii}\right): \\ $$$${k}=\frac{{a}−{h}}{\mathrm{2}{h}}\:\:\:…\left({I}\right) \\ $$$${put}\:\left({I}\right)\:{into}\:\left({i}\right): \\ $$$$\frac{\left({a}−{h}\right)^{\mathrm{2}} }{\mathrm{4}{h}^{\mathrm{2}} }+\left({a}−{h}\right)^{\mathrm{2}} =\frac{\mathrm{3}{s}^{\mathrm{2}} }{\mathrm{4}} \\ $$$$\left(\mathrm{1}+\mathrm{4}{h}^{\mathrm{2}} \right)\left({a}−{h}\right)^{\mathrm{2}} =\mathrm{3}{s}^{\mathrm{2}} {h}^{\mathrm{2}} \\ $$$$\Rightarrow{a}={h}\left(\mathrm{1}+{s}\sqrt{\frac{\mathrm{3}}{\mathrm{1}+\mathrm{4}{h}^{\mathrm{2}} }}\right)\:\:\:…\left({II}\right) \\ $$$${put}\:\:{into}\:\left({iii}\right): \\ $$$$\Rightarrow\mathrm{2}\left(\mathrm{1}+\mathrm{4}{h}^{\mathrm{2}} \right)\left({s}\sqrt{\frac{\mathrm{3}}{\mathrm{1}+\mathrm{4}{h}^{\mathrm{2}} }}−\mathrm{2}{h}^{\mathrm{2}} \right)={s}^{\mathrm{2}} \:\:\:…\left({III}\right) \\ $$$$ \\ $$$${for}\:{a}\:{given}\:{s}\:\left(\leqslant\mathrm{4}.\mathrm{73565}\right)\:{we}\:{get}\:{h}\:{from} \\ $$$$\left({III}\right)\:{and}\:{then}\:{a}\:{from}\:\left({II}\right). \\ $$
Commented by mr W last updated on 12/Dec/20
we see for 0<s<3.4641 there is one possible triangle. for 3.4641≤s≤4.73565 there are two possible triangles. example: s=4
$${we}\:{see}\:{for}\:\mathrm{0}<{s}<\mathrm{3}.\mathrm{4641}\:{there}\:{is}\:{one} \\ $$$${possible}\:{triangle}.\: \\ $$$${for}\:\mathrm{3}.\mathrm{4641}\leqslant{s}\leqslant\mathrm{4}.\mathrm{73565}\:{there}\:{are}\:{two} \\ $$$${possible}\:{triangles}. \\ $$$$ \\ $$$${example}:\:{s}=\mathrm{4} \\ $$
Commented by mr W last updated on 12/Dec/20
Commented by mr W last updated on 12/Dec/20
Commented by mr W last updated on 12/Dec/20
Commented by mr W last updated on 12/Dec/20
Commented by mr W last updated on 12/Dec/20
Answered by ajfour last updated on 12/Dec/20
let eq. of BC be y=2mx+c tan θ=2m Intersection with parabola x^2 −2mx−c=0 x=m±(√(m^2 +c)) midpoint D(m, 2m^2 +c) (x_2 −x_1 )(√(1+4m^2 ))=s ⇒ 4(m^2 +c)(1+4m^2 )=s^2 ...(i) ((s(√3))/2)((1/( (√(1+4m^2 )))))=2m^2 +c ((s(√3))/(2(√(1+4m^2 ))))=m^2 +(s^2 /(4(1+4m^2 ))) ...(ii) x_A =a=m+((s(√3))/2)(((2m)/( (√(1+4m^2 ))))) ...(iii) let 1+4m^2 =t^2 now from (ii) 2(√3)st=(t^2 −1)t^2 +s^2 ⇒ t^4 −t^2 −2(√3)st+s^2 =0 (s−(√3)t)^2 =4t^2 −t^4 s=(√3)t±(√(3t^2 +t^2 −t^4 )) s=t((√3)+(√(4−t^2 ))) s_(max) ≈ 4.7356 Discriminant D=12t^2 −4(t^4 −t^2 ) ≥0 ⇒ t^4 ≤4t^2 ⇒ t^2 =1+4m^2 ≤ 4 ⇒ tan θ=2m ≤ (√3)
$${let}\:{eq}.\:{of}\:{BC}\:{be} \\ $$$${y}=\mathrm{2}{mx}+{c} \\ $$$$\mathrm{tan}\:\theta=\mathrm{2}{m} \\ $$$${Intersection}\:{with}\:{parabola} \\ $$$${x}^{\mathrm{2}} −\mathrm{2}{mx}−{c}=\mathrm{0} \\ $$$${x}={m}\pm\sqrt{{m}^{\mathrm{2}} +{c}} \\ $$$${midpoint}\:{D}\left({m},\:\mathrm{2}{m}^{\mathrm{2}} +{c}\right) \\ $$$$\left({x}_{\mathrm{2}} −{x}_{\mathrm{1}} \right)\sqrt{\mathrm{1}+\mathrm{4}{m}^{\mathrm{2}} }={s}\:\:\:\Rightarrow \\ $$$$\mathrm{4}\left({m}^{\mathrm{2}} +{c}\right)\left(\mathrm{1}+\mathrm{4}{m}^{\mathrm{2}} \right)={s}^{\mathrm{2}} \:\:\:\:…\left({i}\right) \\ $$$$\frac{{s}\sqrt{\mathrm{3}}}{\mathrm{2}}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+\mathrm{4}{m}^{\mathrm{2}} }}\right)=\mathrm{2}{m}^{\mathrm{2}} +{c} \\ $$$$\frac{{s}\sqrt{\mathrm{3}}}{\mathrm{2}\sqrt{\mathrm{1}+\mathrm{4}{m}^{\mathrm{2}} }}={m}^{\mathrm{2}} +\frac{{s}^{\mathrm{2}} }{\mathrm{4}\left(\mathrm{1}+\mathrm{4}{m}^{\mathrm{2}} \right)}\:\:\:…\left({ii}\right) \\ $$$${x}_{{A}} ={a}={m}+\frac{{s}\sqrt{\mathrm{3}}}{\mathrm{2}}\left(\frac{\mathrm{2}{m}}{\:\sqrt{\mathrm{1}+\mathrm{4}{m}^{\mathrm{2}} }}\right)\:\:\:…\left({iii}\right) \\ $$$${let}\:\:\mathrm{1}+\mathrm{4}{m}^{\mathrm{2}} ={t}^{\mathrm{2}} \\ $$$${now}\:\:{from}\:\left({ii}\right) \\ $$$$\mathrm{2}\sqrt{\mathrm{3}}{st}=\left({t}^{\mathrm{2}} −\mathrm{1}\right){t}^{\mathrm{2}} +{s}^{\mathrm{2}} \\ $$$$\Rightarrow\:\:\:{t}^{\mathrm{4}} −{t}^{\mathrm{2}} −\mathrm{2}\sqrt{\mathrm{3}}{st}+{s}^{\mathrm{2}} =\mathrm{0} \\ $$$$\:\:\:\left({s}−\sqrt{\mathrm{3}}{t}\right)^{\mathrm{2}} =\mathrm{4}{t}^{\mathrm{2}} −{t}^{\mathrm{4}} \\ $$$$\:\:{s}=\sqrt{\mathrm{3}}{t}\pm\sqrt{\mathrm{3}{t}^{\mathrm{2}} +{t}^{\mathrm{2}} −{t}^{\mathrm{4}} } \\ $$$$\:\:{s}={t}\left(\sqrt{\mathrm{3}}+\sqrt{\mathrm{4}−{t}^{\mathrm{2}} }\right) \\ $$$$\:\:{s}_{{max}} \approx\:\mathrm{4}.\mathrm{7356} \\ $$$${Discriminant} \\ $$$${D}=\mathrm{12}{t}^{\mathrm{2}} −\mathrm{4}\left({t}^{\mathrm{4}} −{t}^{\mathrm{2}} \right)\:\geqslant\mathrm{0} \\ $$$$\Rightarrow\:\:{t}^{\mathrm{4}} \leqslant\mathrm{4}{t}^{\mathrm{2}} \\ $$$$\Rightarrow\:\:{t}^{\mathrm{2}} =\mathrm{1}+\mathrm{4}{m}^{\mathrm{2}} \:\leqslant\:\mathrm{4} \\ $$$$\Rightarrow\:\:\mathrm{tan}\:\theta=\mathrm{2}{m}\:\leqslant\:\sqrt{\mathrm{3}} \\ $$
Commented by ajfour last updated on 12/Dec/20
Sir, please help checking my solution, our answers for s_(max) differ. Your solution even seems errorless to me.
$${Sir},\:{please}\:{help}\:{checking}\:{my} \\ $$$${solution},\:{our}\:{answers}\:{for}\:{s}_{{max}} \\ $$$${differ}. \\ $$$${Your}\:{solution}\:{even}\:{seems}\:{errorless} \\ $$$${to}\:{me}. \\ $$
Commented by ajfour last updated on 12/Dec/20
Commented by mr W last updated on 12/Dec/20
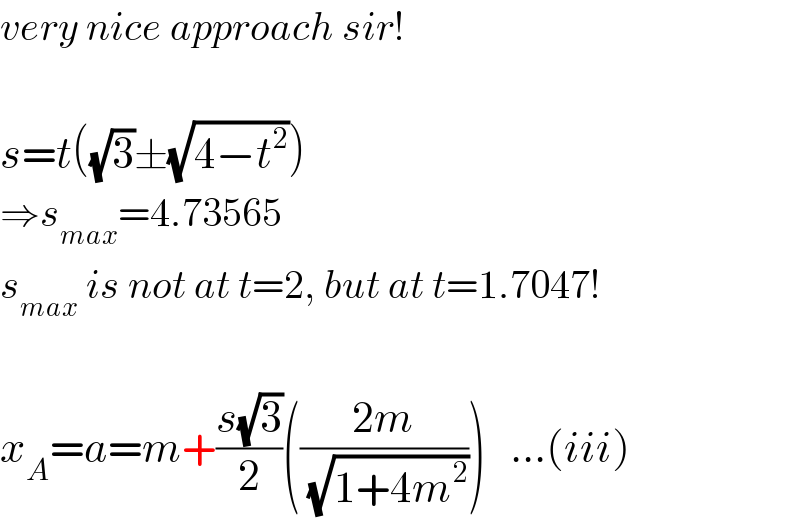
very nice approach sir! s=t((√3)±(√(4−t^2 ))) ⇒s_(max) =4.73565 s_(max) is not at t=2, but at t=1.7047! x_A =a=m+((s(√3))/2)(((2m)/( (√(1+4m^2 ))))) ...(iii)
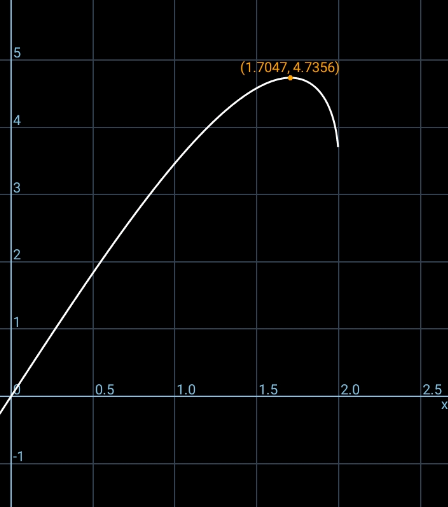
$${very}\:{nice}\:{approach}\:{sir}! \\ $$$$ \\ $$$${s}={t}\left(\sqrt{\mathrm{3}}\pm\sqrt{\mathrm{4}−{t}^{\mathrm{2}} }\right) \\ $$$$\Rightarrow{s}_{{max}} =\mathrm{4}.\mathrm{73565} \\ $$$${s}_{{max}} \:{is}\:{not}\:{at}\:{t}=\mathrm{2},\:{but}\:{at}\:{t}=\mathrm{1}.\mathrm{7047}! \\ $$$$ \\ $$$${x}_{{A}} ={a}={m}+\frac{{s}\sqrt{\mathrm{3}}}{\mathrm{2}}\left(\frac{\mathrm{2}{m}}{\:\sqrt{\mathrm{1}+\mathrm{4}{m}^{\mathrm{2}} }}\right)\:\:\:…\left({iii}\right) \\ $$
Commented by ajfour last updated on 12/Dec/20
thank you Sir.
$${thank}\:{you}\:{Sir}. \\ $$
Commented by mr W last updated on 12/Dec/20
Commented by ajfour last updated on 12/Dec/20
s=f(t)
$$\:\:\:{s}={f}\left({t}\right) \\ $$
Commented by mr W last updated on 12/Dec/20
exact value for s_(max) : s=t((√3)+(√(4−t^2 ))) (ds/dt)=(√3)+2(√(4−t^2 ))−(4/( (√(4−t^2 ))))=0 let x=(√(4−t^2 )) 2x^2 +(√3)x−4=0 ⇒x=(((√(35))−(√3))/4)=(√(4−t^2 )) ⇒t=(√(4−((((√(35))−(√3))/4))^2 )) =((√(2((√(105))+13)))/4)≈1.70466 s_(max) =(√(4−((((√(35))−(√3))/4))^2 ))((√3)+(((√(35))−(√3))/4)) =((√(2(35(√(105))+359)))/8)≈4.73565
$${exact}\:{value}\:{for}\:{s}_{{max}} : \\ $$$${s}={t}\left(\sqrt{\mathrm{3}}+\sqrt{\mathrm{4}−{t}^{\mathrm{2}} }\right) \\ $$$$\frac{{ds}}{{dt}}=\sqrt{\mathrm{3}}+\mathrm{2}\sqrt{\mathrm{4}−{t}^{\mathrm{2}} }−\frac{\mathrm{4}}{\:\sqrt{\mathrm{4}−{t}^{\mathrm{2}} }}=\mathrm{0} \\ $$$${let}\:{x}=\sqrt{\mathrm{4}−{t}^{\mathrm{2}} } \\ $$$$\mathrm{2}{x}^{\mathrm{2}} +\sqrt{\mathrm{3}}{x}−\mathrm{4}=\mathrm{0} \\ $$$$\Rightarrow{x}=\frac{\sqrt{\mathrm{35}}−\sqrt{\mathrm{3}}}{\mathrm{4}}=\sqrt{\mathrm{4}−{t}^{\mathrm{2}} } \\ $$$$\Rightarrow{t}=\sqrt{\mathrm{4}−\left(\frac{\sqrt{\mathrm{35}}−\sqrt{\mathrm{3}}}{\mathrm{4}}\right)^{\mathrm{2}} } \\ $$$$=\frac{\sqrt{\mathrm{2}\left(\sqrt{\mathrm{105}}+\mathrm{13}\right)}}{\mathrm{4}}\approx\mathrm{1}.\mathrm{70466} \\ $$$${s}_{{max}} =\sqrt{\mathrm{4}−\left(\frac{\sqrt{\mathrm{35}}−\sqrt{\mathrm{3}}}{\mathrm{4}}\right)^{\mathrm{2}} }\left(\sqrt{\mathrm{3}}+\frac{\sqrt{\mathrm{35}}−\sqrt{\mathrm{3}}}{\mathrm{4}}\right) \\ $$$$=\frac{\sqrt{\mathrm{2}\left(\mathrm{35}\sqrt{\mathrm{105}}+\mathrm{359}\right)}}{\mathrm{8}}\approx\mathrm{4}.\mathrm{73565} \\ $$
Commented by ajfour last updated on 12/Dec/20
Wonderful, Sir, good analysis!
$${Wonderful},\:{Sir},\:{good}\:{analysis}! \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *