Menu Close

Question-125593

Tinku Tara 0 Comments
Pin




Question Number 125593 by shaker last updated on 12/Dec/20
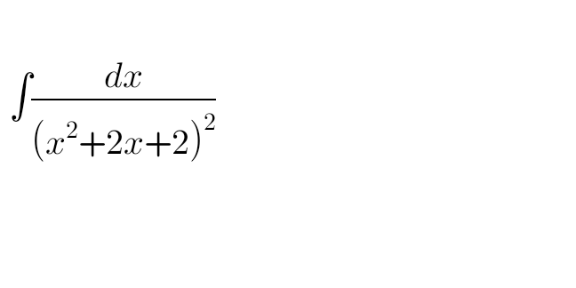
Answered by MJS_new last updated on 12/Dec/20
∫(dx/((x^2 +2x+2)^2 ))= [Ostrogradski′s Method (search the www for it)] =((x+1)/(2(x^2 +2x+2)))+(1/2)∫(dx/(x^2 +2x+2))= =((x+1)/(2(x^2 +2x+2)))+(1/2)arctan (x+1) +C
$$\int\frac{{dx}}{\left({x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{2}\right)^{\mathrm{2}} }= \\ $$$$\:\:\:\:\:\left[\mathrm{Ostrogradski}'\mathrm{s}\:\mathrm{Method}\:\left({search}\:{the}\:{www}\:{for}\:{it}\right)\right] \\ $$$$=\frac{{x}+\mathrm{1}}{\mathrm{2}\left({x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{2}\right)}+\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{dx}}{{x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{2}}= \\ $$$$=\frac{{x}+\mathrm{1}}{\mathrm{2}\left({x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{2}\right)}+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{arctan}\:\left({x}+\mathrm{1}\right)\:+{C} \\ $$
Commented by bemath last updated on 12/Dec/20
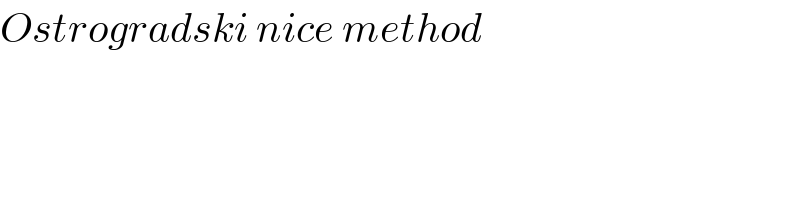
Ostrogradski nice method
$${Ostrogradski}\:{nice}\:{method} \\ $$
Answered by mathmax by abdo last updated on 12/Dec/20
parametric method let f(t)=∫ (dx/(x^2 +2x+t)) with ∣t∣>1 we have f^′ (t)=−∫ (dx/((x^2 +2x+t)^2 ))+c ⇒∫ (dx/((x^2 +2x+2)^2 ))=−f^′ (2)+clet explicit f(t) f(t)=∫ (dx/((x+1)^2 +t−1)) =_(x+1=(√(t−1))u) ∫ (((√(t−1))u)/((t−1)(1+u^2 )))du =(1/( (√(t−1))))∫ (du/(1+u^2 )) =((arctan(((x+1)/( (√(t−1))))))/( (√(t−1)))) =((u(t))/(v(t))) f^′ (t)=((u^′ v−uv^′ )/v^2 ) we have u^′ =(((((x+1)/( (√(t−1)))))^′ )/(1+(((x+1)^2 )/(t−1))))=(((x+1)×(−(1/2))(t−1)^(−(3/2)) )/(((x+1)^2 +t−1)/(t−1))) =−((x+1)/2)(t−1)^(−(1/2)) ×(1/((x+1)^2 +t−1)) =−((x+1)/(2(√(t−1)){(x+1)^2 +t−1})) v^′ =(1/(2(√(t−1)))) ⇒f^′ (t)=((−((x+1)/(2((x+1)^2 +t−1)))−(1/(2(√(t−1))))arctan(((x+1)/( (√(t−1))))))/(t−1)) ⇒f^′ (2)=−((x+1)/(2((x+1)^2 +1)))−(1/2)arctan(x+1) +c ⇒ ∫ (dx/((x^2 +2x+2)^2 ))=−f^′ (2)=((x+1)/(2{(x+1)^2 +1}))+(1/2)arctan(x+1) +C
$$\mathrm{parametric}\:\mathrm{method}\:\mathrm{let}\:\mathrm{f}\left(\mathrm{t}\right)=\int\:\:\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{2x}+\mathrm{t}}\:\:\mathrm{with}\:\mid\mathrm{t}\mid>\mathrm{1} \\ $$$$\mathrm{we}\:\mathrm{have}\:\mathrm{f}^{'} \left(\mathrm{t}\right)=−\int\:\frac{\mathrm{dx}}{\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{2x}+\mathrm{t}\right)^{\mathrm{2}} }+\mathrm{c}\:\Rightarrow\int\:\:\frac{\mathrm{dx}}{\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{2x}+\mathrm{2}\right)^{\mathrm{2}} }=−\mathrm{f}^{'} \left(\mathrm{2}\right)+\mathrm{clet}\:\mathrm{explicit}\:\mathrm{f}\left(\mathrm{t}\right) \\ $$$$\mathrm{f}\left(\mathrm{t}\right)=\int\:\:\frac{\mathrm{dx}}{\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} +\mathrm{t}−\mathrm{1}}\:=_{\mathrm{x}+\mathrm{1}=\sqrt{\mathrm{t}−\mathrm{1}}\mathrm{u}} \:\:\:\:\:\int\:\:\:\frac{\sqrt{\mathrm{t}−\mathrm{1}}\mathrm{u}}{\left(\mathrm{t}−\mathrm{1}\right)\left(\mathrm{1}+\mathrm{u}^{\mathrm{2}} \right)}\mathrm{du} \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{\mathrm{t}−\mathrm{1}}}\int\:\:\frac{\mathrm{du}}{\mathrm{1}+\mathrm{u}^{\mathrm{2}} }\:=\frac{\mathrm{arctan}\left(\frac{\mathrm{x}+\mathrm{1}}{\:\sqrt{\mathrm{t}−\mathrm{1}}}\right)}{\:\sqrt{\mathrm{t}−\mathrm{1}}}\:=\frac{\mathrm{u}\left(\mathrm{t}\right)}{\mathrm{v}\left(\mathrm{t}\right)} \\ $$$$\mathrm{f}^{'} \left(\mathrm{t}\right)=\frac{\mathrm{u}^{'} \mathrm{v}−\mathrm{uv}^{'} }{\mathrm{v}^{\mathrm{2}} }\:\:\mathrm{we}\:\mathrm{have}\:\mathrm{u}^{'} \:=\frac{\left(\frac{\mathrm{x}+\mathrm{1}}{\:\sqrt{\mathrm{t}−\mathrm{1}}}\right)^{'} }{\mathrm{1}+\frac{\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{t}−\mathrm{1}}}=\frac{\left(\mathrm{x}+\mathrm{1}\right)×\left(−\frac{\mathrm{1}}{\mathrm{2}}\right)\left(\mathrm{t}−\mathrm{1}\right)^{−\frac{\mathrm{3}}{\mathrm{2}}} }{\frac{\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} +\mathrm{t}−\mathrm{1}}{\mathrm{t}−\mathrm{1}}} \\ $$$$=−\frac{\mathrm{x}+\mathrm{1}}{\mathrm{2}}\left(\mathrm{t}−\mathrm{1}\right)^{−\frac{\mathrm{1}}{\mathrm{2}}} ×\frac{\mathrm{1}}{\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} +\mathrm{t}−\mathrm{1}}\:=−\frac{\mathrm{x}+\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{t}−\mathrm{1}}\left\{\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} \:+\mathrm{t}−\mathrm{1}\right\}} \\ $$$$\mathrm{v}^{'} =\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{t}−\mathrm{1}}}\:\Rightarrow\mathrm{f}^{'} \left(\mathrm{t}\right)=\frac{−\frac{\mathrm{x}+\mathrm{1}}{\mathrm{2}\left(\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} +\mathrm{t}−\mathrm{1}\right)}−\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{t}−\mathrm{1}}}\mathrm{arctan}\left(\frac{\mathrm{x}+\mathrm{1}}{\:\sqrt{\mathrm{t}−\mathrm{1}}}\right)}{\mathrm{t}−\mathrm{1}} \\ $$$$\Rightarrow\mathrm{f}^{'} \left(\mathrm{2}\right)=−\frac{\mathrm{x}+\mathrm{1}}{\mathrm{2}\left(\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} +\mathrm{1}\right)}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{arctan}\left(\mathrm{x}+\mathrm{1}\right)\:+\mathrm{c}\:\Rightarrow \\ $$$$\int\:\:\frac{\mathrm{dx}}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{2x}+\mathrm{2}\right)^{\mathrm{2}} }=−\mathrm{f}^{'} \left(\mathrm{2}\right)=\frac{\mathrm{x}+\mathrm{1}}{\mathrm{2}\left\{\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} \:+\mathrm{1}\right\}}+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{arctan}\left(\mathrm{x}+\mathrm{1}\right)\:+\mathrm{C} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *