Question Number 125632 by Mathgreat last updated on 12/Dec/20

Answered by snipers237 last updated on 13/Dec/20
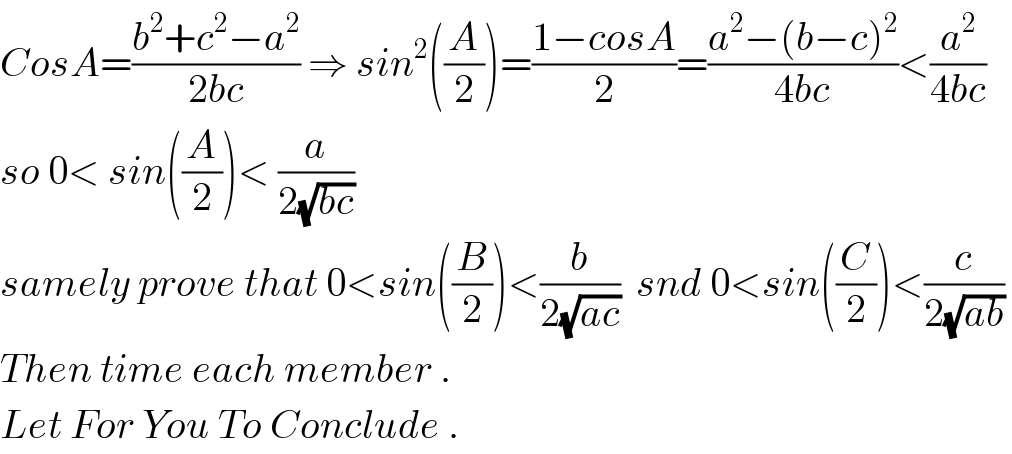
$${CosA}=\frac{{b}^{\mathrm{2}} +{c}^{\mathrm{2}} −{a}^{\mathrm{2}} }{\mathrm{2}{bc}}\:\Rightarrow\:{sin}^{\mathrm{2}} \left(\frac{{A}}{\mathrm{2}}\right)=\frac{\mathrm{1}−{cosA}}{\mathrm{2}}=\frac{{a}^{\mathrm{2}} −\left({b}−{c}\right)^{\mathrm{2}} }{\mathrm{4}{bc}}<\frac{{a}^{\mathrm{2}} }{\mathrm{4}{bc}} \\ $$$${so}\:\mathrm{0}<\:{sin}\left(\frac{{A}}{\mathrm{2}}\right)<\:\frac{{a}}{\mathrm{2}\sqrt{{bc}}}\: \\ $$$${samely}\:{prove}\:{that}\:\mathrm{0}<{sin}\left(\frac{{B}}{\mathrm{2}}\right)<\frac{{b}}{\mathrm{2}\sqrt{{ac}}}\:\:{snd}\:\mathrm{0}<{sin}\left(\frac{{C}}{\mathrm{2}}\right)<\frac{{c}}{\mathrm{2}\sqrt{{ab}}}\: \\ $$$${Then}\:{time}\:{each}\:{member}\:. \\ $$$${Let}\:{For}\:{You}\:{To}\:{Conclude}\:. \\ $$
