Question-125639

Question Number 125639 by aurpeyz last updated on 12/Dec/20

Commented by ZiYangLee last updated on 13/Dec/20

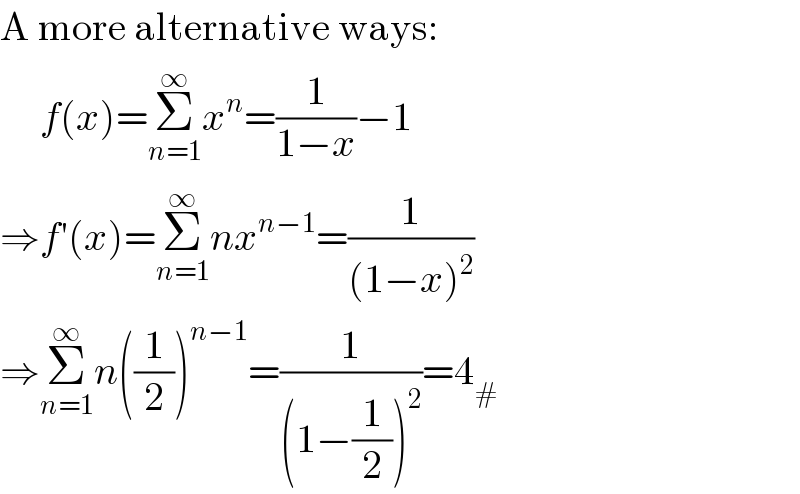
A more alternative ways: f(x)=Σ_(n=1) ^∞ x^n =(1/(1−x))−1 ⇒f′(x)=Σ_(n=1) ^∞ nx^(n−1) =(1/((1−x)^2 )) ⇒Σ_(n=1) ^∞ n((1/2))^(n−1) =(1/((1−(1/2))^2 ))=4_#

$$\mathrm{A}\:\mathrm{more}\:\mathrm{alternative}\:\mathrm{ways}: \\ $$$$\:\:\:\:\:{f}\left({x}\right)=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}{x}^{{n}} =\frac{\mathrm{1}}{\mathrm{1}−{x}}−\mathrm{1} \\ $$$$\Rightarrow{f}'\left({x}\right)=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}{nx}^{{n}−\mathrm{1}} =\frac{\mathrm{1}}{\left(\mathrm{1}−{x}\right)^{\mathrm{2}} } \\ $$$$\Rightarrow\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}{n}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{{n}−\mathrm{1}} =\frac{\mathrm{1}}{\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} }=\mathrm{4}_{#} \\ $$

Commented by aurpeyz last updated on 14/Dec/20

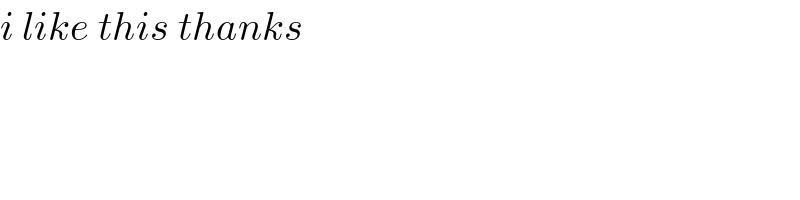
$${i}\:{like}\:{this}\:{thanks} \\ $$

Answered by Dwaipayan Shikari last updated on 12/Dec/20

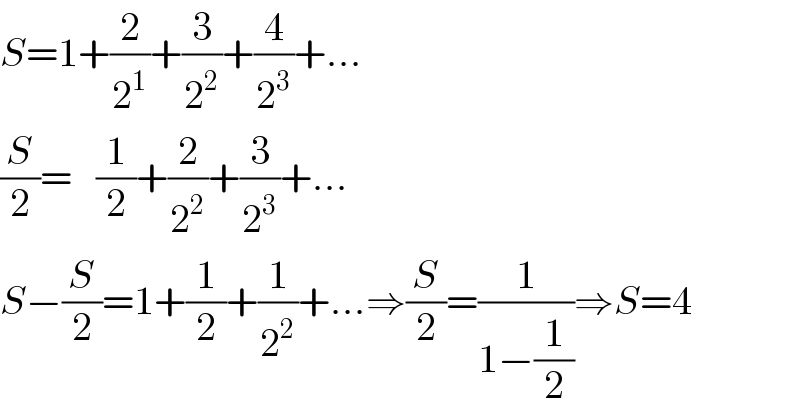
S=1+(2/2^1 )+(3/2^2 )+(4/2^3 )+... (S/2)= (1/2)+(2/2^2 )+(3/2^3 )+... S−(S/2)=1+(1/2)+(1/2^2 )+...⇒(S/2)=(1/(1−(1/2)))⇒S=4

$${S}=\mathrm{1}+\frac{\mathrm{2}}{\mathrm{2}^{\mathrm{1}} }+\frac{\mathrm{3}}{\mathrm{2}^{\mathrm{2}} }+\frac{\mathrm{4}}{\mathrm{2}^{\mathrm{3}} }+… \\ $$$$\frac{{S}}{\mathrm{2}}=\:\:\:\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{2}}{\mathrm{2}^{\mathrm{2}} }+\frac{\mathrm{3}}{\mathrm{2}^{\mathrm{3}} }+… \\ $$$${S}−\frac{{S}}{\mathrm{2}}=\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }+…\Rightarrow\frac{{S}}{\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}}\Rightarrow{S}=\mathrm{4} \\ $$

Commented by aurpeyz last updated on 12/Dec/20

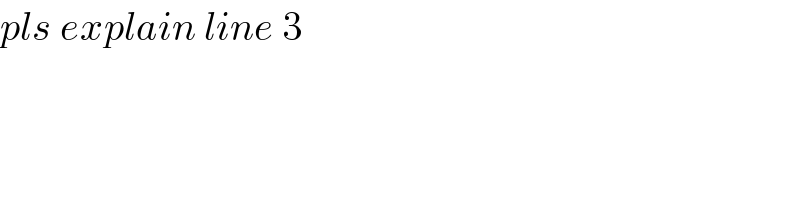
$${pls}\:{explain}\:{line}\:\mathrm{3} \\ $$

Commented by Dwaipayan Shikari last updated on 12/Dec/20

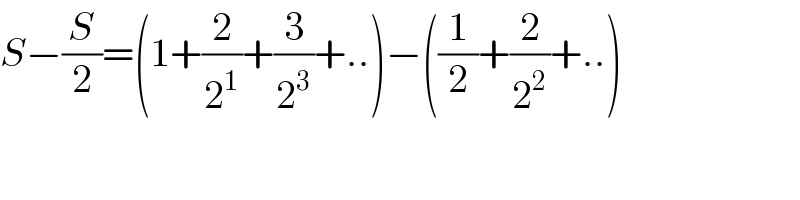
S−(S/2)=(1+(2/2^1 )+(3/2^3 )+..)−((1/2)+(2/2^2 )+..)

$${S}−\frac{{S}}{\mathrm{2}}=\left(\mathrm{1}+\frac{\mathrm{2}}{\mathrm{2}^{\mathrm{1}} }+\frac{\mathrm{3}}{\mathrm{2}^{\mathrm{3}} }+..\right)−\left(\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{2}}{\mathrm{2}^{\mathrm{2}} }+..\right) \\ $$

Commented by aurpeyz last updated on 12/Dec/20

$${thanks} \\ $$

Answered by mathmax by abdo last updated on 12/Dec/20

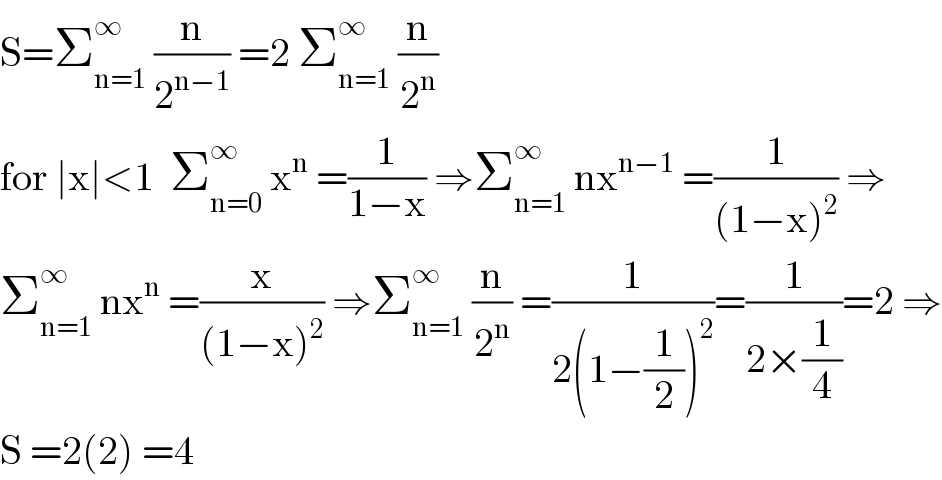
S=Σ_(n=1) ^∞ (n/2^(n−1) ) =2 Σ_(n=1) ^∞ (n/2^n ) for ∣x∣<1 Σ_(n=0) ^∞ x^n =(1/(1−x)) ⇒Σ_(n=1) ^∞ nx^(n−1) =(1/((1−x)^2 )) ⇒ Σ_(n=1) ^∞ nx^n =(x/((1−x)^2 )) ⇒Σ_(n=1) ^∞ (n/2^n ) =(1/(2(1−(1/2))^2 ))=(1/(2×(1/4)))=2 ⇒ S =2(2) =4

$$\mathrm{S}=\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{n}}{\mathrm{2}^{\mathrm{n}−\mathrm{1}} }\:=\mathrm{2}\:\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{n}}{\mathrm{2}^{\mathrm{n}} } \\ $$$$\mathrm{for}\:\mid\mathrm{x}\mid<\mathrm{1}\:\:\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\mathrm{x}^{\mathrm{n}} \:=\frac{\mathrm{1}}{\mathrm{1}−\mathrm{x}}\:\Rightarrow\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\mathrm{nx}^{\mathrm{n}−\mathrm{1}} \:=\frac{\mathrm{1}}{\left(\mathrm{1}−\mathrm{x}\right)^{\mathrm{2}} }\:\Rightarrow \\ $$$$\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\mathrm{nx}^{\mathrm{n}} \:=\frac{\mathrm{x}}{\left(\mathrm{1}−\mathrm{x}\right)^{\mathrm{2}} }\:\Rightarrow\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{n}}{\mathrm{2}^{\mathrm{n}} }\:=\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{2}×\frac{\mathrm{1}}{\mathrm{4}}}=\mathrm{2}\:\Rightarrow \\ $$$$\mathrm{S}\:=\mathrm{2}\left(\mathrm{2}\right)\:=\mathrm{4} \\ $$

Commented by aurpeyz last updated on 13/Dec/20

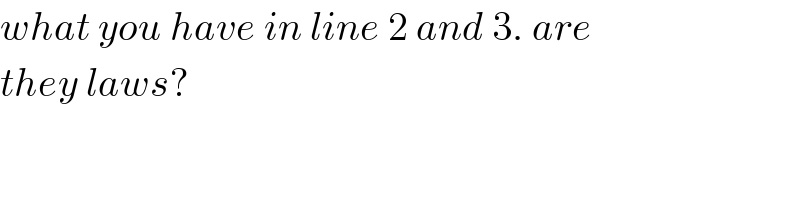
what you have in line 2 and 3. are they laws?

$${what}\:{you}\:{have}\:{in}\:{line}\:\mathrm{2}\:{and}\:\mathrm{3}.\:{are}\: \\ $$$${they}\:{laws}? \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply