Question Number 125641 by aurpeyz last updated on 12/Dec/20
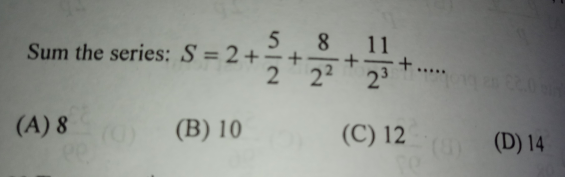
Answered by Dwaipayan Shikari last updated on 12/Dec/20
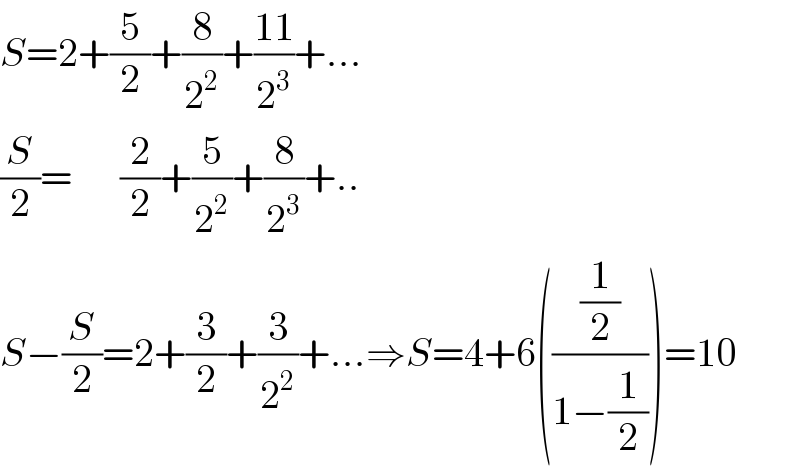
$${S}=\mathrm{2}+\frac{\mathrm{5}}{\mathrm{2}}+\frac{\mathrm{8}}{\mathrm{2}^{\mathrm{2}} }+\frac{\mathrm{11}}{\mathrm{2}^{\mathrm{3}} }+… \\ $$$$\frac{{S}}{\mathrm{2}}=\:\:\:\:\:\:\frac{\mathrm{2}}{\mathrm{2}}+\frac{\mathrm{5}}{\mathrm{2}^{\mathrm{2}} }+\frac{\mathrm{8}}{\mathrm{2}^{\mathrm{3}} }+.. \\ $$$${S}−\frac{{S}}{\mathrm{2}}=\mathrm{2}+\frac{\mathrm{3}}{\mathrm{2}}+\frac{\mathrm{3}}{\mathrm{2}^{\mathrm{2}} }+…\Rightarrow{S}=\mathrm{4}+\mathrm{6}\left(\frac{\frac{\mathrm{1}}{\mathrm{2}}}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}}\right)=\mathrm{10} \\ $$
Commented by aurpeyz last updated on 12/Dec/20

$${thanks} \\ $$
Answered by mathmax by abdo last updated on 12/Dec/20
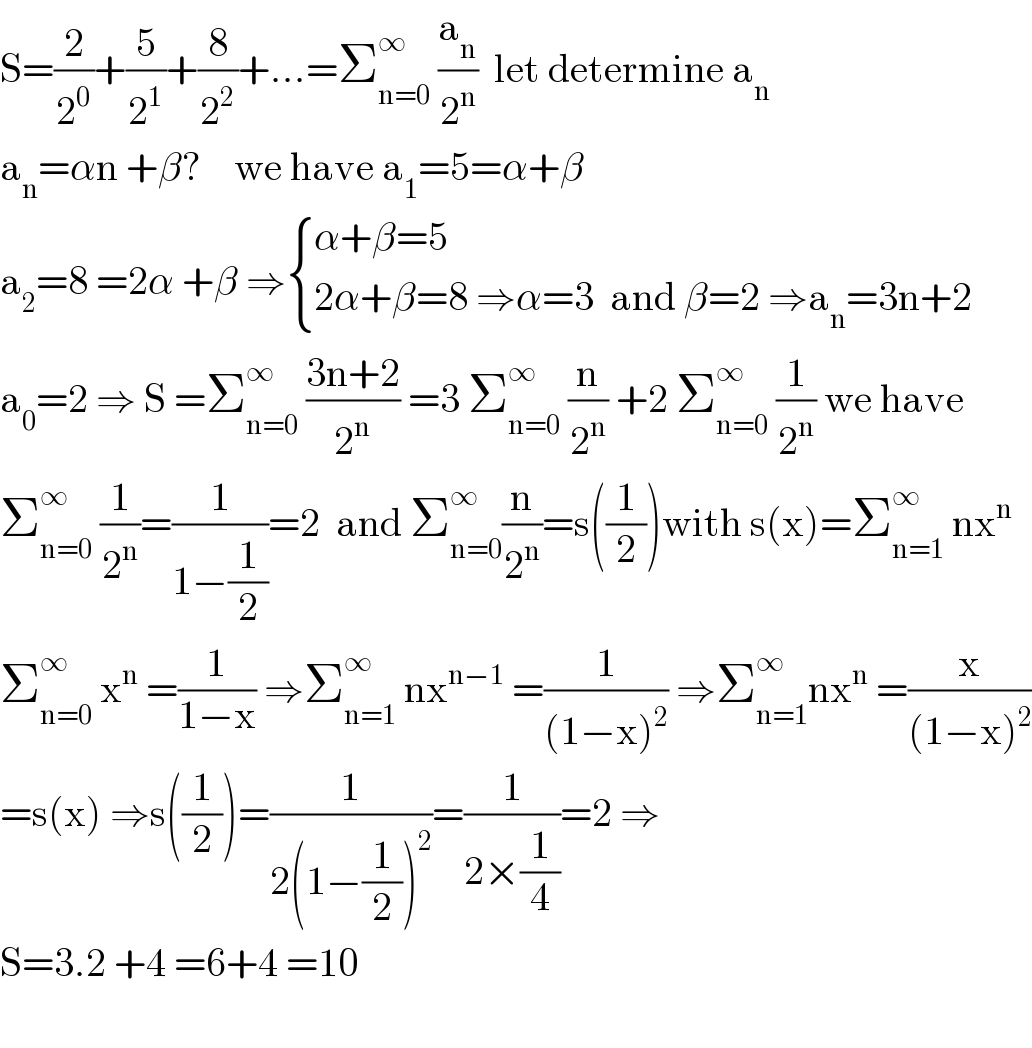
$$\mathrm{S}=\frac{\mathrm{2}}{\mathrm{2}^{\mathrm{0}} }+\frac{\mathrm{5}}{\mathrm{2}^{\mathrm{1}} }+\frac{\mathrm{8}}{\mathrm{2}^{\mathrm{2}} }+…=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{a}_{\mathrm{n}} }{\mathrm{2}^{\mathrm{n}} }\:\:\mathrm{let}\:\mathrm{determine}\:\mathrm{a}_{\mathrm{n}} \\ $$$$\mathrm{a}_{\mathrm{n}} =\alpha\mathrm{n}\:+\beta?\:\:\:\:\mathrm{we}\:\mathrm{have}\:\mathrm{a}_{\mathrm{1}} =\mathrm{5}=\alpha+\beta \\ $$$$\mathrm{a}_{\mathrm{2}} =\mathrm{8}\:=\mathrm{2}\alpha\:+\beta\:\Rightarrow\begin{cases}{\alpha+\beta=\mathrm{5}}\\{\mathrm{2}\alpha+\beta=\mathrm{8}\:\Rightarrow\alpha=\mathrm{3}\:\:\mathrm{and}\:\beta=\mathrm{2}\:\Rightarrow\mathrm{a}_{\mathrm{n}} =\mathrm{3n}+\mathrm{2}}\end{cases} \\ $$$$\mathrm{a}_{\mathrm{0}} =\mathrm{2}\:\Rightarrow\:\mathrm{S}\:=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{3n}+\mathrm{2}}{\mathrm{2}^{\mathrm{n}} }\:=\mathrm{3}\:\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{n}}{\mathrm{2}^{\mathrm{n}} }\:+\mathrm{2}\:\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{n}} }\:\mathrm{we}\:\mathrm{have} \\ $$$$\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{n}} }=\frac{\mathrm{1}}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}}=\mathrm{2}\:\:\mathrm{and}\:\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \frac{\mathrm{n}}{\mathrm{2}^{\mathrm{n}} }=\mathrm{s}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\mathrm{with}\:\mathrm{s}\left(\mathrm{x}\right)=\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\mathrm{nx}^{\mathrm{n}} \\ $$$$\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\mathrm{x}^{\mathrm{n}} \:=\frac{\mathrm{1}}{\mathrm{1}−\mathrm{x}}\:\Rightarrow\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\mathrm{nx}^{\mathrm{n}−\mathrm{1}} \:=\frac{\mathrm{1}}{\left(\mathrm{1}−\mathrm{x}\right)^{\mathrm{2}} }\:\Rightarrow\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \mathrm{nx}^{\mathrm{n}} \:=\frac{\mathrm{x}}{\left(\mathrm{1}−\mathrm{x}\right)^{\mathrm{2}} } \\ $$$$=\mathrm{s}\left(\mathrm{x}\right)\:\Rightarrow\mathrm{s}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)=\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{2}×\frac{\mathrm{1}}{\mathrm{4}}}=\mathrm{2}\:\Rightarrow \\ $$$$\mathrm{S}=\mathrm{3}.\mathrm{2}\:+\mathrm{4}\:=\mathrm{6}+\mathrm{4}\:=\mathrm{10} \\ $$$$ \\ $$
Commented by aurpeyz last updated on 13/Dec/20
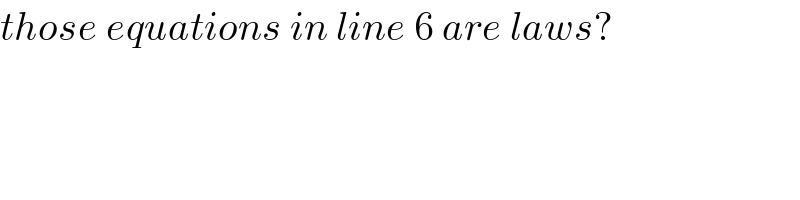
$${those}\:{equations}\:{in}\:{line}\:\mathrm{6}\:{are}\:{laws}? \\ $$
