Question Number 125673 by aurpeyz last updated on 12/Dec/20

Answered by bramlexs22 last updated on 13/Dec/20
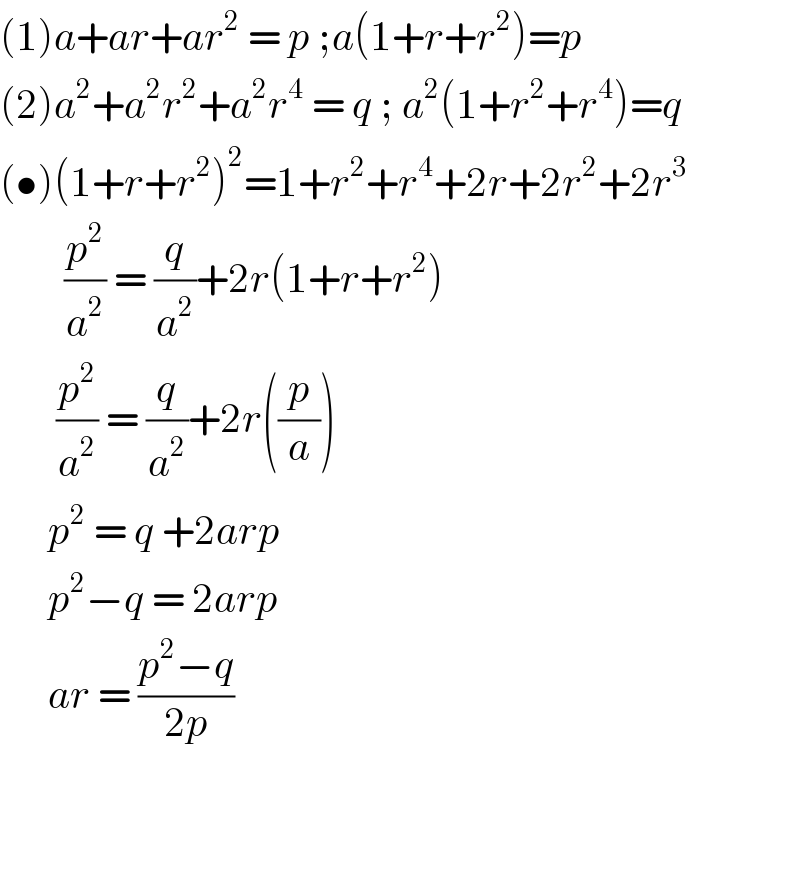
$$\left(\mathrm{1}\right){a}+{ar}+{ar}^{\mathrm{2}} \:=\:{p}\:;{a}\left(\mathrm{1}+{r}+{r}^{\mathrm{2}} \right)={p} \\ $$$$\left(\mathrm{2}\right){a}^{\mathrm{2}} +{a}^{\mathrm{2}} {r}^{\mathrm{2}} +{a}^{\mathrm{2}} {r}^{\mathrm{4}} \:=\:{q}\:;\:{a}^{\mathrm{2}} \left(\mathrm{1}+{r}^{\mathrm{2}} +{r}^{\mathrm{4}} \right)={q} \\ $$$$\left(\bullet\right)\left(\mathrm{1}+{r}+{r}^{\mathrm{2}} \right)^{\mathrm{2}} =\mathrm{1}+{r}^{\mathrm{2}} +{r}^{\mathrm{4}} +\mathrm{2}{r}+\mathrm{2}{r}^{\mathrm{2}} +\mathrm{2}{r}^{\mathrm{3}} \\ $$$$\:\:\:\:\:\:\:\:\frac{{p}^{\mathrm{2}} }{{a}^{\mathrm{2}} }\:=\:\frac{{q}}{{a}^{\mathrm{2}} }+\mathrm{2}{r}\left(\mathrm{1}+{r}+{r}^{\mathrm{2}} \right) \\ $$$$\:\:\:\:\:\:\:\frac{{p}^{\mathrm{2}} }{{a}^{\mathrm{2}} }\:=\:\frac{{q}}{{a}^{\mathrm{2}} }+\mathrm{2}{r}\left(\frac{{p}}{{a}}\right) \\ $$$$\:\:\:\:\:\:{p}^{\mathrm{2}} \:=\:{q}\:+\mathrm{2}{arp} \\ $$$$\:\:\:\:\:\:{p}^{\mathrm{2}} −{q}\:=\:\mathrm{2}{arp} \\ $$$$\:\:\:\:\:\:{ar}\:=\:\frac{{p}^{\mathrm{2}} −{q}}{\mathrm{2}{p}} \\ $$$$ \\ $$$$ \\ $$
Commented by aurpeyz last updated on 13/Dec/20

$${thanks} \\ $$
