Question Number 125981 by 0731619177 last updated on 16/Dec/20
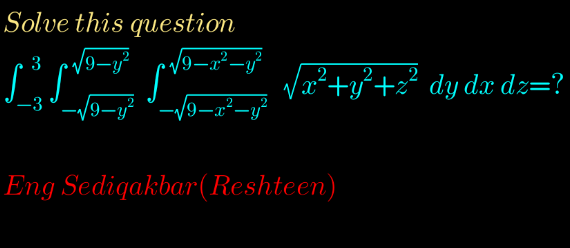
Answered by snipers237 last updated on 16/Dec/20
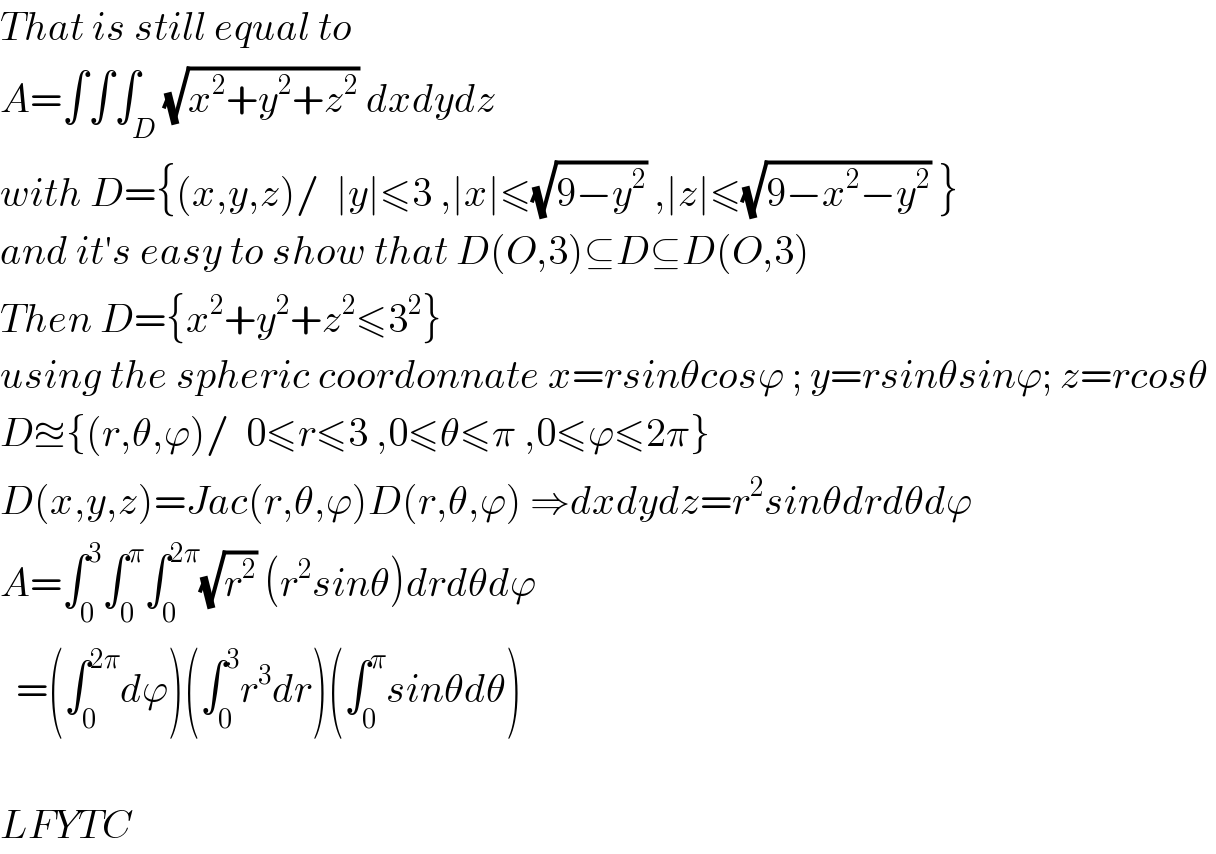
$${That}\:{is}\:{still}\:{equal}\:{to}\: \\ $$$${A}=\int\int\int_{{D}} \sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{z}^{\mathrm{2}} }\:{dxdydz} \\ $$$${with}\:{D}=\left\{\left({x},{y},{z}\right)/\:\:\mid{y}\mid\leqslant\mathrm{3}\:,\mid{x}\mid\leqslant\sqrt{\mathrm{9}−{y}^{\mathrm{2}} }\:,\mid{z}\mid\leqslant\sqrt{\mathrm{9}−{x}^{\mathrm{2}} −{y}^{\mathrm{2}} }\:\right\} \\ $$$${and}\:{it}'{s}\:{easy}\:{to}\:{show}\:{that}\:{D}\left({O},\mathrm{3}\right)\subseteq{D}\subseteq{D}\left({O},\mathrm{3}\right) \\ $$$${Then}\:{D}=\left\{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{z}^{\mathrm{2}} \leqslant\mathrm{3}^{\mathrm{2}} \right\}\: \\ $$$${using}\:{the}\:{spheric}\:{coordonnate}\:{x}={rsin}\theta{cos}\varphi\:;\:{y}={rsin}\theta{sin}\varphi;\:{z}={rcos}\theta\: \\ $$$${D}\approxeq\left\{\left({r},\theta,\varphi\right)/\:\:\mathrm{0}\leqslant{r}\leqslant\mathrm{3}\:,\mathrm{0}\leqslant\theta\leqslant\pi\:,\mathrm{0}\leqslant\varphi\leqslant\mathrm{2}\pi\right\} \\ $$$${D}\left({x},{y},{z}\right)={Jac}\left({r},\theta,\varphi\right){D}\left({r},\theta,\varphi\right)\:\Rightarrow{dxdydz}={r}^{\mathrm{2}} {sin}\theta{drd}\theta{d}\varphi \\ $$$${A}=\int_{\mathrm{0}} ^{\mathrm{3}} \int_{\mathrm{0}} ^{\pi} \int_{\mathrm{0}} ^{\mathrm{2}\pi} \sqrt{{r}^{\mathrm{2}} }\:\left({r}^{\mathrm{2}} {sin}\theta\right){drd}\theta{d}\varphi \\ $$$$\:\:=\left(\int_{\mathrm{0}} ^{\mathrm{2}\pi} {d}\varphi\right)\left(\int_{\mathrm{0}} ^{\mathrm{3}} {r}^{\mathrm{3}} {dr}\right)\left(\int_{\mathrm{0}} ^{\pi} {sin}\theta{d}\theta\right) \\ $$$$ \\ $$$${LFYTC} \\ $$
