Question Number 126010 by bramlexs22 last updated on 16/Dec/20

Answered by liberty last updated on 16/Dec/20
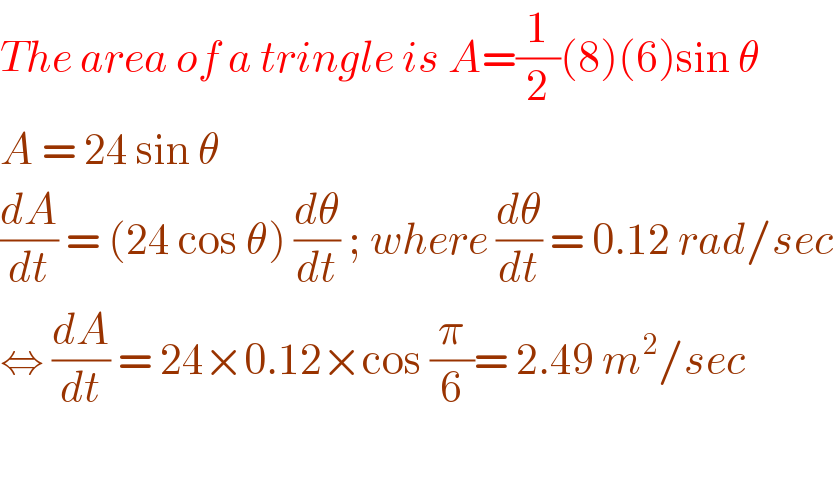
$${The}\:{area}\:{of}\:{a}\:{tringle}\:{is}\:{A}=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{8}\right)\left(\mathrm{6}\right)\mathrm{sin}\:\theta \\ $$$${A}\:=\:\mathrm{24}\:\mathrm{sin}\:\theta \\ $$$$\frac{{dA}}{{dt}}\:=\:\left(\mathrm{24}\:\mathrm{cos}\:\theta\right)\:\frac{{d}\theta}{{dt}}\:;\:{where}\:\frac{{d}\theta}{{dt}}\:=\:\mathrm{0}.\mathrm{12}\:{rad}/{sec} \\ $$$$\Leftrightarrow\:\frac{{dA}}{{dt}}\:=\:\mathrm{24}×\mathrm{0}.\mathrm{12}×\mathrm{cos}\:\frac{\pi}{\mathrm{6}}=\:\mathrm{2}.\mathrm{49}\:{m}^{\mathrm{2}} /{sec}\: \\ $$$$ \\ $$
