Question Number 126080 by ajfour last updated on 17/Dec/20
Commented by ajfour last updated on 18/Dec/20

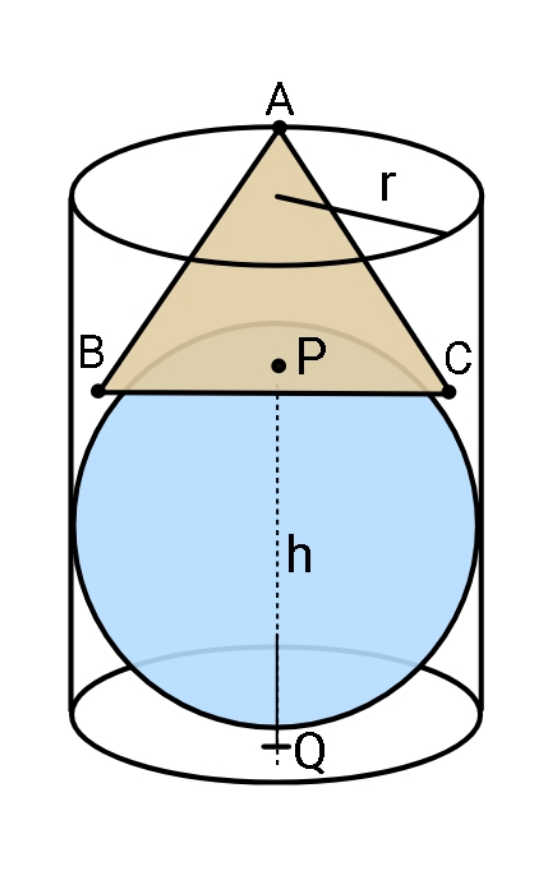
$${Cylinder}\:{and}\:{sphere}\:{have}\:{the} \\ $$$${same}\:{radius}.\:{An}\:{equilateral} \\ $$$${triangular}\:{plate}\:{rests}\:{on}\:{sphere} \\ $$$${with}\:{two}\:{vertices}\:{against}\:{curved} \\ $$$${surface}\:{of}\:{cylinder}\:{and}\:{top}\:{vertex} \\ $$$${on}\:{rim}\:{of}\:{cylinder}.\:{It}\:{is}\:{in}\:{contact} \\ $$$${with}\:{sphere}\:{at}\:{point}\:{P}\:{which}\:{is}\:{at} \\ $$$${a}\:{height}\:\boldsymbol{{h}}\:{from}\:{base}\:{of}\:{cylinder}. \\ $$$$\left({PQ}={h}\right).\:\:{Find}\:{height}\:{of}\:{cylinder}. \\ $$
Commented by mr W last updated on 17/Dec/20

$${if}\:{the}\:{top}\:{vertex}\:{has}\:{contact}\:{force} \\ $$$${with}\:{the}\:{rim}\:{of}\:{cylinder},\:{no}\:{unique} \\ $$$${solution}\:{exists}.\:{if}\:{we}\:{assume}\:{that} \\ $$$${the}\:{top}\:{vertex}\:{is}\:{just}\:{on}\:{the}\:{rim},\:{but} \\ $$$${without}\:{real}\:{contact},\:{then}\:{i}\:{think} \\ $$$${there}\:{is}\:{an}\:{unique}\:{solution}.\:{please} \\ $$$${check}\:{sir}. \\ $$
Commented by ajfour last updated on 18/Dec/20

$${triangle}\:{is}\:{oriented}\:{symmetrically} \\ $$$${left}\:{and}\:{right},\:{and}\:{top}\:{vertex}\:{just} \\ $$$${reaching}\:{the}\:{rim},\:{no}\:{contact}\:{force}. \\ $$$$\left({I}\:{get}\:{your}\:{point},\:{Sir},\:{lets}\:{assume}\right. \\ $$$${frictionless}\:{surfaces}\:{of}\:{sphere}, \\ $$$$\left.{triangular}\:{plate}\:{and}\:{cylinder}\right). \\ $$
Answered by mr W last updated on 17/Dec/20
Commented by mr W last updated on 17/Dec/20
![s=side length of equilateral triangle B′=midpoint of BC D=center of mass of plate AB′=(((√3)s)/2) AD=(2/3)×(((√3)s)/2)=(((√3)s)/3) DB′=(1/3)×(((√3)s)/2)=(((√3)s)/6) h=r+r sin θ ⇒sin θ=(h/r)−1 2r=(((√3)s)/2)×sin θ+r−(√(r^2 −(s^2 /4))) ⇒(((√3)s)/2)×((h/r)−1)−r=(√(r^2 −(s^2 /4))) ⇒[3((h/r)−1)^2 +1]s=4(√3)((h/r)−1)r ⇒s=((4(√3)((h/r)−1)r)/(3((h/r)−1)^2 +1)) PD=SD×cos θ=DB′×cos^2 θ =(((√3)s)/6)[1−((h/r)−1)^2 ] AP=AD+PD=(((√3)s)/3)+(((√3)s)/6)[1−((h/r)−1)^2 ] =(((√3)s)/6)[3−((h/r)−1)^2 ] height of cylinder=H H=h+AP×cos θ ⇒H=h+(((√3)s)/6)[3−((h/r)−1)^2 ](√(1−((h/r)−1)^2 ))](https://www.tinkutara.com/question/Q126176.png)
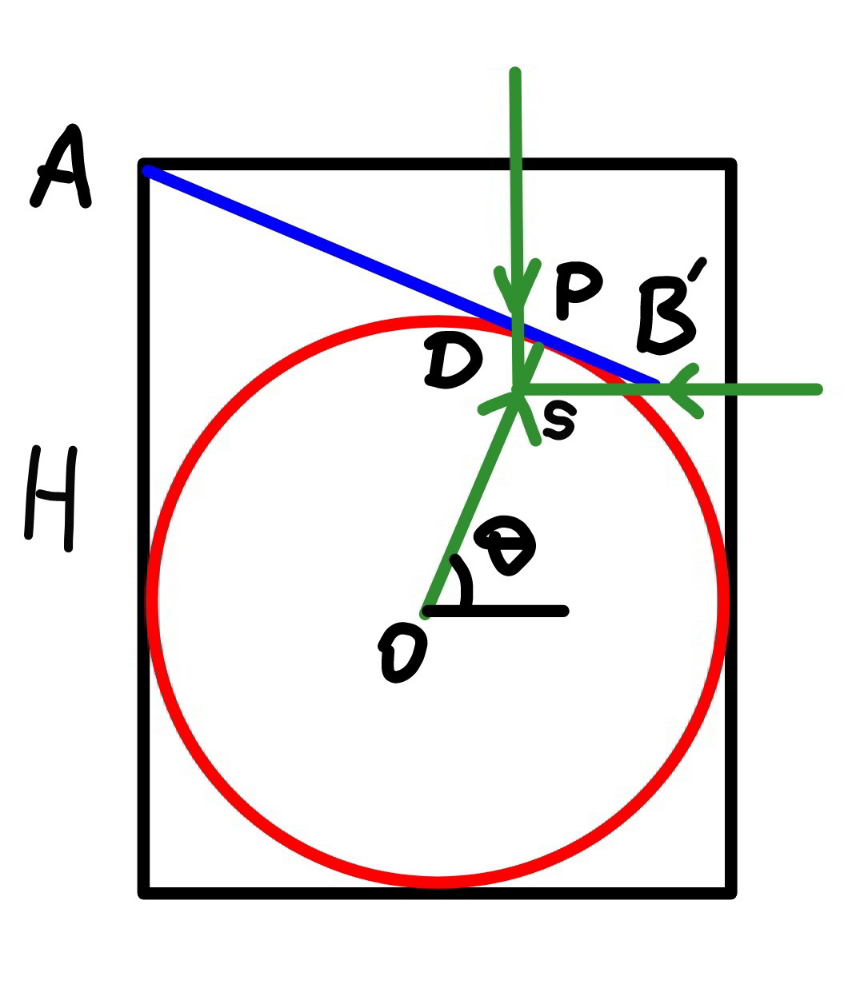
$${s}={side}\:{length}\:{of}\:{equilateral}\:{triangle} \\ $$$${B}'={midpoint}\:{of}\:{BC} \\ $$$${D}={center}\:{of}\:{mass}\:{of}\:{plate} \\ $$$${AB}'=\frac{\sqrt{\mathrm{3}}{s}}{\mathrm{2}} \\ $$$${AD}=\frac{\mathrm{2}}{\mathrm{3}}×\frac{\sqrt{\mathrm{3}}{s}}{\mathrm{2}}=\frac{\sqrt{\mathrm{3}}{s}}{\mathrm{3}} \\ $$$${DB}'=\frac{\mathrm{1}}{\mathrm{3}}×\frac{\sqrt{\mathrm{3}}{s}}{\mathrm{2}}=\frac{\sqrt{\mathrm{3}}{s}}{\mathrm{6}} \\ $$$${h}={r}+{r}\:\mathrm{sin}\:\theta \\ $$$$\Rightarrow\mathrm{sin}\:\theta=\frac{{h}}{{r}}−\mathrm{1} \\ $$$$\mathrm{2}{r}=\frac{\sqrt{\mathrm{3}}{s}}{\mathrm{2}}×\mathrm{sin}\:\theta+{r}−\sqrt{{r}^{\mathrm{2}} −\frac{{s}^{\mathrm{2}} }{\mathrm{4}}} \\ $$$$\Rightarrow\frac{\sqrt{\mathrm{3}}{s}}{\mathrm{2}}×\left(\frac{{h}}{{r}}−\mathrm{1}\right)−{r}=\sqrt{{r}^{\mathrm{2}} −\frac{{s}^{\mathrm{2}} }{\mathrm{4}}} \\ $$$$\Rightarrow\left[\mathrm{3}\left(\frac{{h}}{{r}}−\mathrm{1}\right)^{\mathrm{2}} +\mathrm{1}\right]{s}=\mathrm{4}\sqrt{\mathrm{3}}\left(\frac{{h}}{{r}}−\mathrm{1}\right){r} \\ $$$$\Rightarrow{s}=\frac{\mathrm{4}\sqrt{\mathrm{3}}\left(\frac{{h}}{{r}}−\mathrm{1}\right){r}}{\mathrm{3}\left(\frac{{h}}{{r}}−\mathrm{1}\right)^{\mathrm{2}} +\mathrm{1}} \\ $$$${PD}={SD}×\mathrm{cos}\:\theta={DB}'×\mathrm{cos}^{\mathrm{2}} \:\theta \\ $$$$=\frac{\sqrt{\mathrm{3}}{s}}{\mathrm{6}}\left[\mathrm{1}−\left(\frac{{h}}{{r}}−\mathrm{1}\right)^{\mathrm{2}} \right] \\ $$$${AP}={AD}+{PD}=\frac{\sqrt{\mathrm{3}}{s}}{\mathrm{3}}+\frac{\sqrt{\mathrm{3}}{s}}{\mathrm{6}}\left[\mathrm{1}−\left(\frac{{h}}{{r}}−\mathrm{1}\right)^{\mathrm{2}} \right] \\ $$$$=\frac{\sqrt{\mathrm{3}}{s}}{\mathrm{6}}\left[\mathrm{3}−\left(\frac{{h}}{{r}}−\mathrm{1}\right)^{\mathrm{2}} \right] \\ $$$${height}\:{of}\:{cylinder}={H} \\ $$$${H}={h}+{AP}×\mathrm{cos}\:\theta \\ $$$$\Rightarrow{H}={h}+\frac{\sqrt{\mathrm{3}}{s}}{\mathrm{6}}\left[\mathrm{3}−\left(\frac{{h}}{{r}}−\mathrm{1}\right)^{\mathrm{2}} \right]\sqrt{\mathrm{1}−\left(\frac{{h}}{{r}}−\mathrm{1}\right)^{\mathrm{2}} } \\ $$
Commented by ajfour last updated on 18/Dec/20
$${Very}\:{smart}\:\left({intelligent}\right)\:{diagram} \\ $$$${and}\:{solution}\:{Sir},\:{loved}\:{following} \\ $$$${it};\:\mathcal{TAL}\:\left({thanks}\:{a}\:{lot}\right)! \\ $$
Commented by mr W last updated on 18/Dec/20
$${i}\:{think}\:{in}\:\mathrm{3}{D},\:{but}\:{can}\:{only}\:{illustrate} \\ $$$${with}\:\mathrm{2}{D}−{diagrams}.\:{i}\:{like}\:{your}\:\mathrm{3}{D}− \\ $$$${diagrams}! \\ $$
