Question Number 126097 by amns last updated on 17/Dec/20
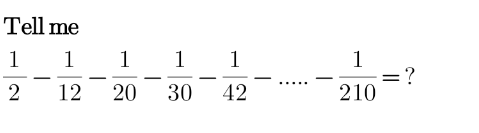
Commented by amns last updated on 17/Dec/20
$$\mathrm{I}\:\mathrm{need}\:\mathrm{someone}'\mathrm{s}\:\mathrm{help}\:\mathrm{to}\:\mathrm{solve}\:\mathrm{it}!!! \\ $$
Answered by Dwaipayan Shikari last updated on 17/Dec/20
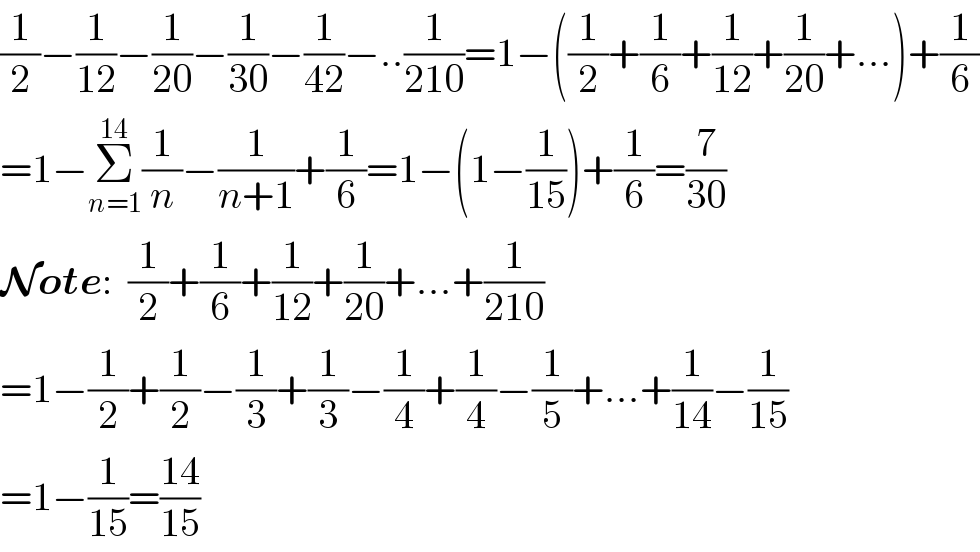
$$\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{12}}−\frac{\mathrm{1}}{\mathrm{20}}−\frac{\mathrm{1}}{\mathrm{30}}−\frac{\mathrm{1}}{\mathrm{42}}−..\frac{\mathrm{1}}{\mathrm{210}}=\mathrm{1}−\left(\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{6}}+\frac{\mathrm{1}}{\mathrm{12}}+\frac{\mathrm{1}}{\mathrm{20}}+…\right)+\frac{\mathrm{1}}{\mathrm{6}} \\ $$$$=\mathrm{1}−\underset{{n}=\mathrm{1}} {\overset{\mathrm{14}} {\sum}}\frac{\mathrm{1}}{{n}}−\frac{\mathrm{1}}{{n}+\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{6}}=\mathrm{1}−\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{15}}\right)+\frac{\mathrm{1}}{\mathrm{6}}=\frac{\mathrm{7}}{\mathrm{30}} \\ $$$$\boldsymbol{\mathcal{N}{ote}}:\:\:\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{6}}+\frac{\mathrm{1}}{\mathrm{12}}+\frac{\mathrm{1}}{\mathrm{20}}+…+\frac{\mathrm{1}}{\mathrm{210}} \\ $$$$=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{5}}+…+\frac{\mathrm{1}}{\mathrm{14}}−\frac{\mathrm{1}}{\mathrm{15}} \\ $$$$=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{15}}=\frac{\mathrm{14}}{\mathrm{15}} \\ $$
