Question-126133

Question Number 126133 by I want to learn more last updated on 17/Dec/20

Answered by Dwaipayan Shikari last updated on 17/Dec/20

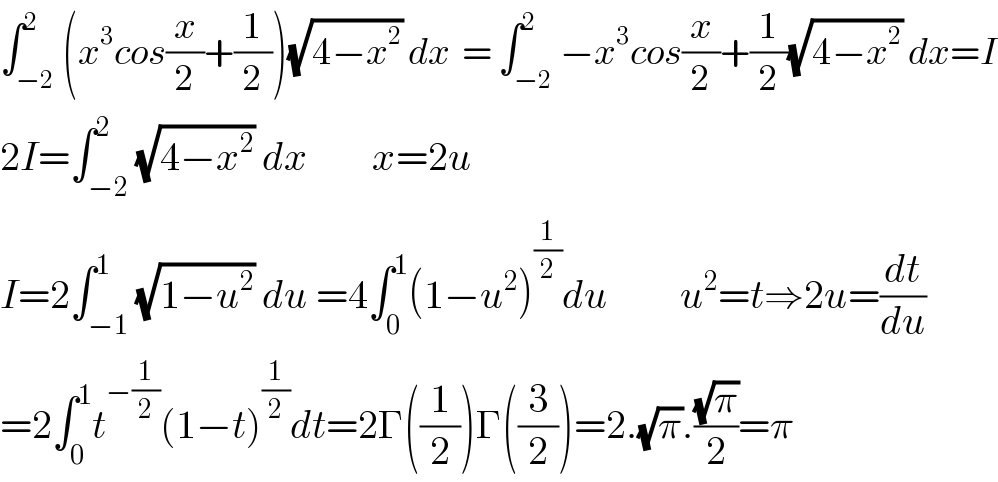
∫_(−2) ^2 (x^3 cos(x/2)+(1/2))(√(4−x^2 )) dx = ∫_(−2) ^2 −x^3 cos(x/2)+(1/2)(√(4−x^2 )) dx=I 2I=∫_(−2) ^2 (√(4−x^2 )) dx x=2u I=2∫_(−1) ^1 (√(1−u^2 )) du =4∫_0 ^1 (1−u^2 )^(1/2) du u^2 =t⇒2u=(dt/du) =2∫_0 ^1 t^(−(1/2)) (1−t)^(1/2) dt=2Γ((1/2))Γ((3/2))=2.(√π).((√π)/2)=π

$$\int_{−\mathrm{2}} ^{\mathrm{2}} \left({x}^{\mathrm{3}} {cos}\frac{{x}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}\right)\sqrt{\mathrm{4}−{x}^{\mathrm{2}} }\:{dx}\:\:=\:\int_{−\mathrm{2}} ^{\mathrm{2}} −{x}^{\mathrm{3}} {cos}\frac{{x}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\mathrm{4}−{x}^{\mathrm{2}} }\:{dx}={I} \\ $$$$\mathrm{2}{I}=\int_{−\mathrm{2}} ^{\mathrm{2}} \sqrt{\mathrm{4}−{x}^{\mathrm{2}} }\:{dx}\:\:\:\:\:\:\:\:{x}=\mathrm{2}{u} \\ $$$${I}=\mathrm{2}\int_{−\mathrm{1}} ^{\mathrm{1}} \sqrt{\mathrm{1}−{u}^{\mathrm{2}} }\:{du}\:=\mathrm{4}\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}−{u}^{\mathrm{2}} \right)^{\frac{\mathrm{1}}{\mathrm{2}}} {du}\:\:\:\:\:\:\:\:\:{u}^{\mathrm{2}} ={t}\Rightarrow\mathrm{2}{u}=\frac{{dt}}{{du}} \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} {t}^{−\frac{\mathrm{1}}{\mathrm{2}}} \left(\mathrm{1}−{t}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} {dt}=\mathrm{2}\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\Gamma\left(\frac{\mathrm{3}}{\mathrm{2}}\right)=\mathrm{2}.\sqrt{\pi}.\frac{\sqrt{\pi}}{\mathrm{2}}=\pi \\ $$

Commented by I want to learn more last updated on 17/Dec/20

Thanks sir, but i don′t understand the steps. the first step precisely.

$$\mathrm{Thanks}\:\mathrm{sir},\:\mathrm{but}\:\mathrm{i}\:\mathrm{don}'\mathrm{t}\:\mathrm{understand}\:\mathrm{the}\:\mathrm{steps}.\:\mathrm{the}\:\mathrm{first}\:\mathrm{step}\:\mathrm{precisely}. \\ $$

Commented by Dwaipayan Shikari last updated on 17/Dec/20

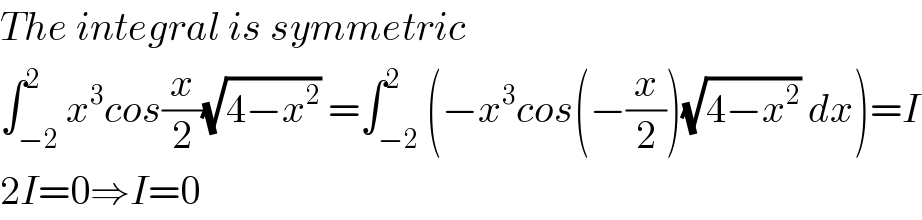
The integral is symmetric ∫_(−2) ^2 x^3 cos(x/2)(√(4−x^2 )) =∫_(−2) ^2 (−x^3 cos(−(x/2))(√(4−x^2 )) dx)=I 2I=0⇒I=0

$${The}\:{integral}\:{is}\:{symmetric}\: \\ $$$$\int_{−\mathrm{2}} ^{\mathrm{2}} {x}^{\mathrm{3}} {cos}\frac{{x}}{\mathrm{2}}\sqrt{\mathrm{4}−{x}^{\mathrm{2}} }\:=\int_{−\mathrm{2}} ^{\mathrm{2}} \left(−{x}^{\mathrm{3}} {cos}\left(−\frac{{x}}{\mathrm{2}}\right)\sqrt{\mathrm{4}−{x}^{\mathrm{2}} }\:{dx}\right)={I} \\ $$$$\mathrm{2}{I}=\mathrm{0}\Rightarrow{I}=\mathrm{0} \\ $$

Commented by I want to learn more last updated on 17/Dec/20

$$\mathrm{I}\:\mathrm{appreciate}\:\mathrm{sir}. \\ $$

Commented by mathmax by abdo last updated on 17/Dec/20

$$\mathrm{not}\:\mathrm{correct}! \\ $$

Answered by mathmax by abdo last updated on 17/Dec/20

I=∫_(−2) ^2 (x^3 cos((x/2))+(1/2))(√(4−x^2 ))dx ⇒ I =∫_(−2) ^2 x^3 cos((x/2))(√(1−x^2 ))dx +(1/2)∫_(−2) ^2 (√(4−x^2 ))dx but ∫_(−2) ^2 x^3 cos((x/2))(√(1−x^2 ))dx=0(function under integral is odd) ⇒I=∫_0 ^2 (√(4−x^2 ))dx =_(x=2sinθ) ∫_0 ^(π/2) 2 cosθ (2cosθ)dθ =4 ∫_0 ^(π/2) cos^2 θ dθ =4∫_0 ^(π/2) ((1+cos(2θ))/2)dθ =2∫_0 ^(π/2) (1+cos(2θ)dθ =2[θ +(1/2)sin(2θ)]_0 ^(π/2) =2.(π/2)=π

$$\mathrm{I}=\int_{−\mathrm{2}} ^{\mathrm{2}} \left(\mathrm{x}^{\mathrm{3}} \:\mathrm{cos}\left(\frac{\mathrm{x}}{\mathrm{2}}\right)+\frac{\mathrm{1}}{\mathrm{2}}\right)\sqrt{\mathrm{4}−\mathrm{x}^{\mathrm{2}} }\mathrm{dx}\:\Rightarrow \\ $$$$\mathrm{I}\:=\int_{−\mathrm{2}} ^{\mathrm{2}} \mathrm{x}^{\mathrm{3}} \mathrm{cos}\left(\frac{\mathrm{x}}{\mathrm{2}}\right)\sqrt{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }\mathrm{dx}\:+\frac{\mathrm{1}}{\mathrm{2}}\int_{−\mathrm{2}} ^{\mathrm{2}} \sqrt{\mathrm{4}−\mathrm{x}^{\mathrm{2}} }\mathrm{dx}\:\:\mathrm{but} \\ $$$$\int_{−\mathrm{2}} ^{\mathrm{2}} \:\mathrm{x}^{\mathrm{3}} \mathrm{cos}\left(\frac{\mathrm{x}}{\mathrm{2}}\right)\sqrt{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }\mathrm{dx}=\mathrm{0}\left(\mathrm{function}\:\mathrm{under}\:\mathrm{integral}\:\mathrm{is}\:\mathrm{odd}\right) \\ $$$$\Rightarrow\mathrm{I}=\int_{\mathrm{0}} ^{\mathrm{2}} \sqrt{\mathrm{4}−\mathrm{x}^{\mathrm{2}} }\mathrm{dx}\:=_{\mathrm{x}=\mathrm{2sin}\theta} \:\:\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{2}\:\mathrm{cos}\theta\:\left(\mathrm{2cos}\theta\right)\mathrm{d}\theta \\ $$$$=\mathrm{4}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\mathrm{cos}^{\mathrm{2}} \theta\:\mathrm{d}\theta\:=\mathrm{4}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{1}+\mathrm{cos}\left(\mathrm{2}\theta\right)}{\mathrm{2}}\mathrm{d}\theta\:=\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left(\mathrm{1}+\mathrm{cos}\left(\mathrm{2}\theta\right)\mathrm{d}\theta\right. \\ $$$$=\mathrm{2}\left[\theta\:+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\left(\mathrm{2}\theta\right)\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:=\mathrm{2}.\frac{\pi}{\mathrm{2}}=\pi \\ $$

Commented by I want to learn more last updated on 20/Dec/20

$$\mathrm{Thanks}\:\mathrm{sir}. \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply