Question Number 126192 by ajfour last updated on 18/Dec/20

Commented by ajfour last updated on 18/Dec/20

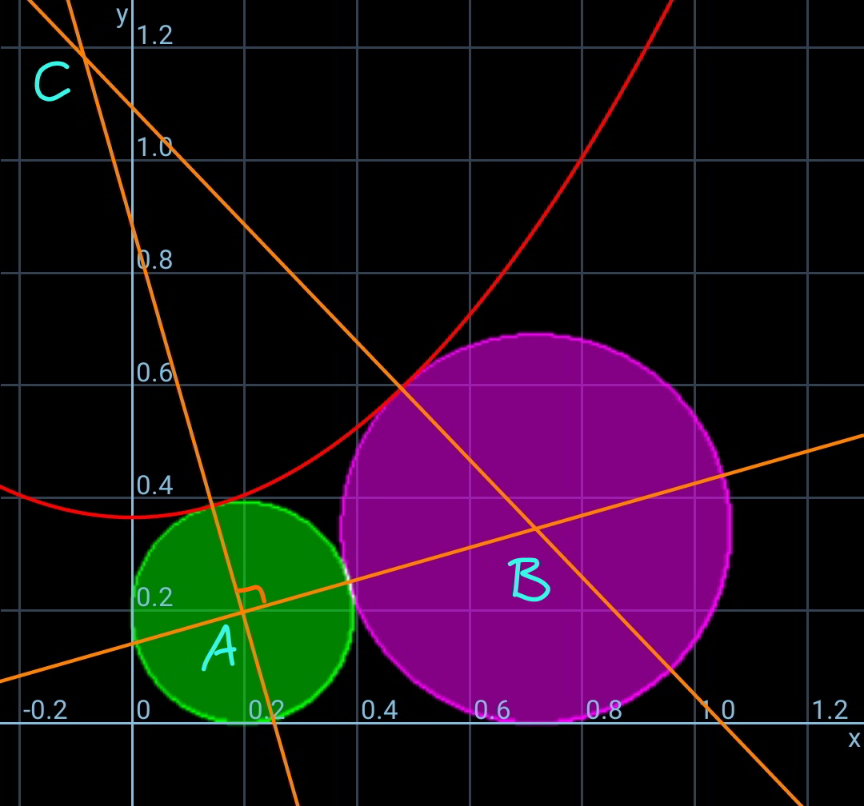
$${If}\:{shape}\:{of}\:{parabola}\:{is}\:{same}\:{as} \\ $$$${that}\:{of}\:{y}={x}^{\mathrm{2}} ,\:{find}\:\:{radius}\:{of} \\ $$$${the}\:{smaller}\:{circle}. \\ $$
Commented by MJS_new last updated on 19/Dec/20

$$\mathrm{I}\:\mathrm{get} \\ $$$${r}_{{A}} \approx.\mathrm{196437} \\ $$$${r}_{{B}} \approx.\mathrm{344870} \\ $$$$\mathrm{par}:\:{y}={x}^{\mathrm{2}} +.\mathrm{365017} \\ $$
Commented by MJS_new last updated on 19/Dec/20
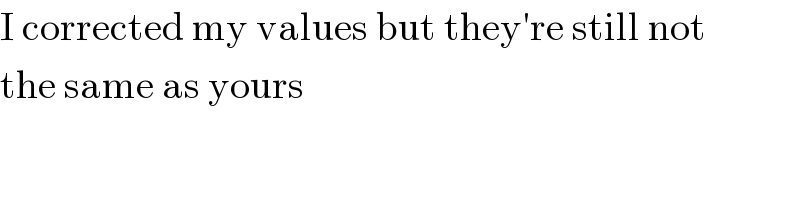
$$\mathrm{I}\:\mathrm{corrected}\:\mathrm{my}\:\mathrm{values}\:\mathrm{but}\:\mathrm{they}'\mathrm{re}\:\mathrm{still}\:\mathrm{not} \\ $$$$\mathrm{the}\:\mathrm{same}\:\mathrm{as}\:\mathrm{yours} \\ $$
Commented by mr W last updated on 19/Dec/20
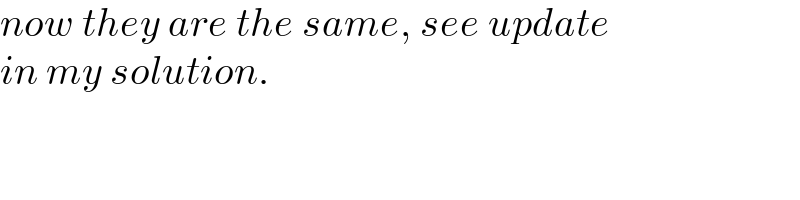
$${now}\:{they}\:{are}\:{the}\:{same},\:{see}\:{update} \\ $$$${in}\:{my}\:{solution}. \\ $$
Commented by MJS_new last updated on 20/Dec/20

$$\mathrm{yes}. \\ $$
Answered by mr W last updated on 18/Dec/20

Commented by mr W last updated on 20/Dec/20
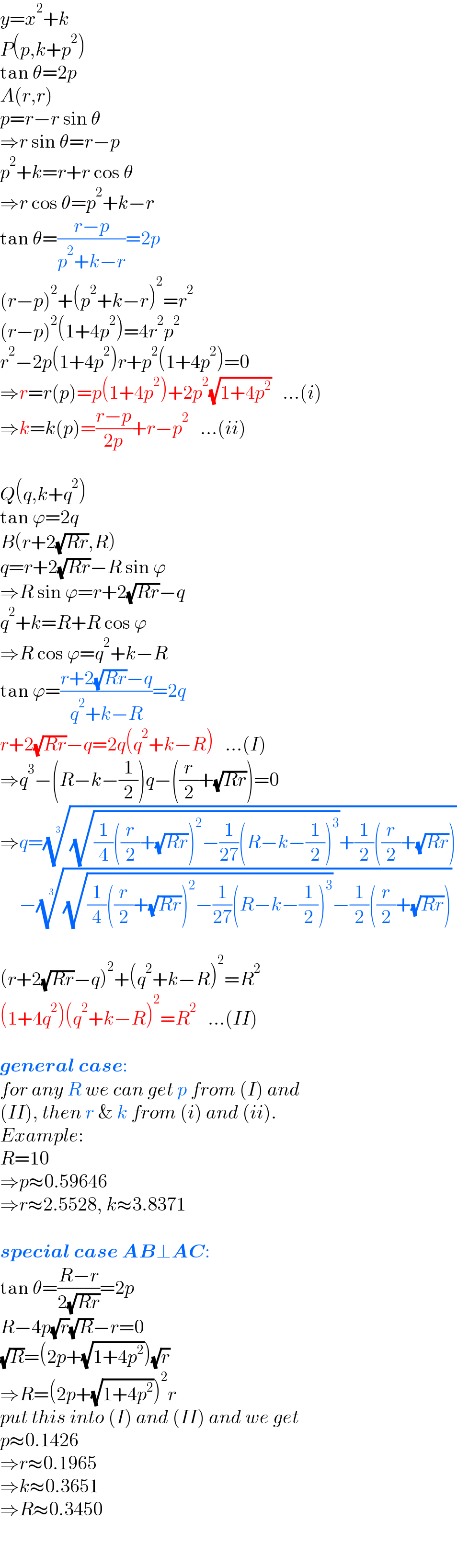
$${y}={x}^{\mathrm{2}} +{k} \\ $$$${P}\left({p},{k}+{p}^{\mathrm{2}} \right) \\ $$$$\mathrm{tan}\:\theta=\mathrm{2}{p} \\ $$$${A}\left({r},{r}\right) \\ $$$${p}={r}−{r}\:\mathrm{sin}\:\theta \\ $$$$\Rightarrow{r}\:\mathrm{sin}\:\theta={r}−{p} \\ $$$${p}^{\mathrm{2}} +{k}={r}+{r}\:\mathrm{cos}\:\theta \\ $$$$\Rightarrow{r}\:\mathrm{cos}\:\theta={p}^{\mathrm{2}} +{k}−{r} \\ $$$$\mathrm{tan}\:\theta=\frac{{r}−{p}}{{p}^{\mathrm{2}} +{k}−{r}}=\mathrm{2}{p} \\ $$$$\left({r}−{p}\right)^{\mathrm{2}} +\left({p}^{\mathrm{2}} +{k}−{r}\right)^{\mathrm{2}} ={r}^{\mathrm{2}} \\ $$$$\left({r}−{p}\right)^{\mathrm{2}} \left(\mathrm{1}+\mathrm{4}{p}^{\mathrm{2}} \right)=\mathrm{4}{r}^{\mathrm{2}} {p}^{\mathrm{2}} \\ $$$${r}^{\mathrm{2}} −\mathrm{2}{p}\left(\mathrm{1}+\mathrm{4}{p}^{\mathrm{2}} \right){r}+{p}^{\mathrm{2}} \left(\mathrm{1}+\mathrm{4}{p}^{\mathrm{2}} \right)=\mathrm{0} \\ $$$$\Rightarrow{r}={r}\left({p}\right)={p}\left(\mathrm{1}+\mathrm{4}{p}^{\mathrm{2}} \right)+\mathrm{2}{p}^{\mathrm{2}} \sqrt{\mathrm{1}+\mathrm{4}{p}^{\mathrm{2}} }\:\:\:…\left({i}\right) \\ $$$$\Rightarrow{k}={k}\left({p}\right)=\frac{{r}−{p}}{\mathrm{2}{p}}+{r}−{p}^{\mathrm{2}} \:\:\:…\left({ii}\right) \\ $$$$ \\ $$$${Q}\left({q},{k}+{q}^{\mathrm{2}} \right) \\ $$$$\mathrm{tan}\:\varphi=\mathrm{2}{q} \\ $$$${B}\left({r}+\mathrm{2}\sqrt{{Rr}},{R}\right) \\ $$$${q}={r}+\mathrm{2}\sqrt{{Rr}}−{R}\:\mathrm{sin}\:\varphi \\ $$$$\Rightarrow{R}\:\mathrm{sin}\:\varphi={r}+\mathrm{2}\sqrt{{Rr}}−{q} \\ $$$${q}^{\mathrm{2}} +{k}={R}+{R}\:\mathrm{cos}\:\varphi \\ $$$$\Rightarrow{R}\:\mathrm{cos}\:\varphi={q}^{\mathrm{2}} +{k}−{R} \\ $$$$\mathrm{tan}\:\varphi=\frac{{r}+\mathrm{2}\sqrt{{Rr}}−{q}}{{q}^{\mathrm{2}} +{k}−{R}}=\mathrm{2}{q} \\ $$$${r}+\mathrm{2}\sqrt{{Rr}}−{q}=\mathrm{2}{q}\left({q}^{\mathrm{2}} +{k}−{R}\right)\:\:\:…\left({I}\right) \\ $$$$\Rightarrow{q}^{\mathrm{3}} −\left({R}−{k}−\frac{\mathrm{1}}{\mathrm{2}}\right){q}−\left(\frac{{r}}{\mathrm{2}}+\sqrt{{Rr}}\right)=\mathrm{0} \\ $$$$\Rightarrow{q}=\sqrt[{\mathrm{3}}]{\sqrt{\frac{\mathrm{1}}{\mathrm{4}}\left(\frac{{r}}{\mathrm{2}}+\sqrt{{Rr}}\right)^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{27}}\left({R}−{k}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{3}} }+\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{{r}}{\mathrm{2}}+\sqrt{{Rr}}\right)} \\ $$$$\:\:\:\:\:−\sqrt[{\mathrm{3}}]{\sqrt{\frac{\mathrm{1}}{\mathrm{4}}\left(\frac{{r}}{\mathrm{2}}+\sqrt{{Rr}}\right)^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{27}}\left({R}−{k}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{3}} }−\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{{r}}{\mathrm{2}}+\sqrt{{Rr}}\right)} \\ $$$$ \\ $$$$\left({r}+\mathrm{2}\sqrt{{Rr}}−{q}\right)^{\mathrm{2}} +\left({q}^{\mathrm{2}} +{k}−{R}\right)^{\mathrm{2}} ={R}^{\mathrm{2}} \\ $$$$\left(\mathrm{1}+\mathrm{4}{q}^{\mathrm{2}} \right)\left({q}^{\mathrm{2}} +{k}−{R}\right)^{\mathrm{2}} ={R}^{\mathrm{2}} \:\:\:…\left({II}\right) \\ $$$$ \\ $$$$\boldsymbol{{general}}\:\boldsymbol{{case}}: \\ $$$${for}\:{any}\:{R}\:{we}\:{can}\:{get}\:{p}\:{from}\:\left({I}\right)\:{and} \\ $$$$\left({II}\right),\:{then}\:{r}\:\&\:{k}\:{from}\:\left({i}\right)\:{and}\:\left({ii}\right). \\ $$$${Example}: \\ $$$${R}=\mathrm{10} \\ $$$$\Rightarrow{p}\approx\mathrm{0}.\mathrm{59646} \\ $$$$\Rightarrow{r}\approx\mathrm{2}.\mathrm{5528},\:{k}\approx\mathrm{3}.\mathrm{8371} \\ $$$$ \\ $$$$\boldsymbol{{special}}\:\boldsymbol{{case}}\:\boldsymbol{{AB}}\bot\boldsymbol{{AC}}: \\ $$$$\mathrm{tan}\:\theta=\frac{{R}−{r}}{\mathrm{2}\sqrt{{Rr}}}=\mathrm{2}{p} \\ $$$${R}−\mathrm{4}{p}\sqrt{{r}}\sqrt{{R}}−{r}=\mathrm{0} \\ $$$$\sqrt{{R}}=\left(\mathrm{2}{p}+\sqrt{\mathrm{1}+\mathrm{4}{p}^{\mathrm{2}} }\right)\sqrt{{r}} \\ $$$$\Rightarrow{R}=\left(\mathrm{2}{p}+\sqrt{\mathrm{1}+\mathrm{4}{p}^{\mathrm{2}} }\right)^{\mathrm{2}} {r} \\ $$$${put}\:{this}\:{into}\:\left({I}\right)\:{and}\:\left({II}\right)\:{and}\:{we}\:{get} \\ $$$${p}\approx\mathrm{0}.\mathrm{1426} \\ $$$$\Rightarrow{r}\approx\mathrm{0}.\mathrm{1965} \\ $$$$\Rightarrow{k}\approx\mathrm{0}.\mathrm{3651} \\ $$$$\Rightarrow{R}\approx\mathrm{0}.\mathrm{3450} \\ $$
Commented by mr W last updated on 20/Dec/20

Commented by mr W last updated on 20/Dec/20

Commented by mr W last updated on 19/Dec/20