Question Number 126274 by bramlexs22 last updated on 19/Dec/20
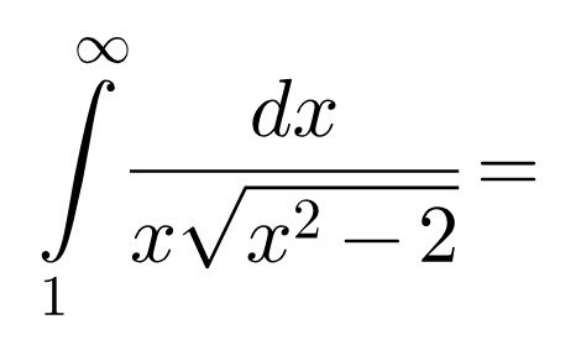
Answered by liberty last updated on 19/Dec/20
![letting x=(√2) sec ℓ with → { ((ℓ=(π/2))),((ℓ=(π/4))) :} ∫_(π/4) ^( π/2) (((√2) sec ℓ tan ℓ)/( (√2) sec ℓ (√(2tan^2 ℓ)))) dℓ = (1/( (√2)))∫ dℓ = (1/( (√2))) [ (π/2)−(π/4) ] = (π/(4(√2))) = ((π(√2))/8)](https://www.tinkutara.com/question/Q126275.png)
$$\:{letting}\:{x}=\sqrt{\mathrm{2}}\:\mathrm{sec}\:\ell\:{with}\:\rightarrow\begin{cases}{\ell=\frac{\pi}{\mathrm{2}}}\\{\ell=\frac{\pi}{\mathrm{4}}}\end{cases} \\ $$$$\:\int_{\pi/\mathrm{4}} ^{\:\pi/\mathrm{2}} \:\frac{\sqrt{\mathrm{2}}\:\mathrm{sec}\:\ell\:\mathrm{tan}\:\ell}{\:\sqrt{\mathrm{2}}\:\mathrm{sec}\:\ell\:\sqrt{\mathrm{2tan}\:^{\mathrm{2}} \ell}}\:{d}\ell\:= \\ $$$$\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\int\:{d}\ell\:=\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\:\left[\:\frac{\pi}{\mathrm{2}}−\frac{\pi}{\mathrm{4}}\:\right]\:=\:\frac{\pi}{\mathrm{4}\sqrt{\mathrm{2}}}\:=\:\frac{\pi\sqrt{\mathrm{2}}}{\mathrm{8}}\: \\ $$
Answered by mathmax by abdo last updated on 19/Dec/20
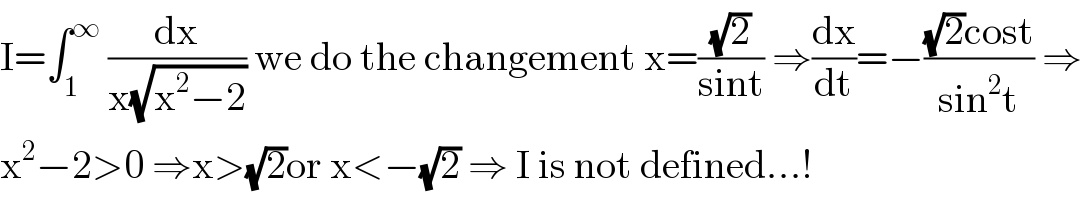
$$\mathrm{I}=\int_{\mathrm{1}} ^{\infty} \:\frac{\mathrm{dx}}{\mathrm{x}\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{2}}}\:\mathrm{we}\:\mathrm{do}\:\mathrm{the}\:\mathrm{changement}\:\mathrm{x}=\frac{\sqrt{\mathrm{2}}}{\mathrm{sint}}\:\Rightarrow\frac{\mathrm{dx}}{\mathrm{dt}}=−\frac{\sqrt{\mathrm{2}}\mathrm{cost}}{\mathrm{sin}^{\mathrm{2}} \mathrm{t}}\:\Rightarrow \\ $$$$\mathrm{x}^{\mathrm{2}} −\mathrm{2}>\mathrm{0}\:\Rightarrow\mathrm{x}>\sqrt{\mathrm{2}}\mathrm{or}\:\mathrm{x}<−\sqrt{\mathrm{2}}\:\Rightarrow\:\mathrm{I}\:\mathrm{is}\:\mathrm{not}\:\mathrm{defined}…! \\ $$
