Question-126329

Question Number 126329 by mnjuly1970 last updated on 19/Dec/20

Answered by Olaf last updated on 19/Dec/20

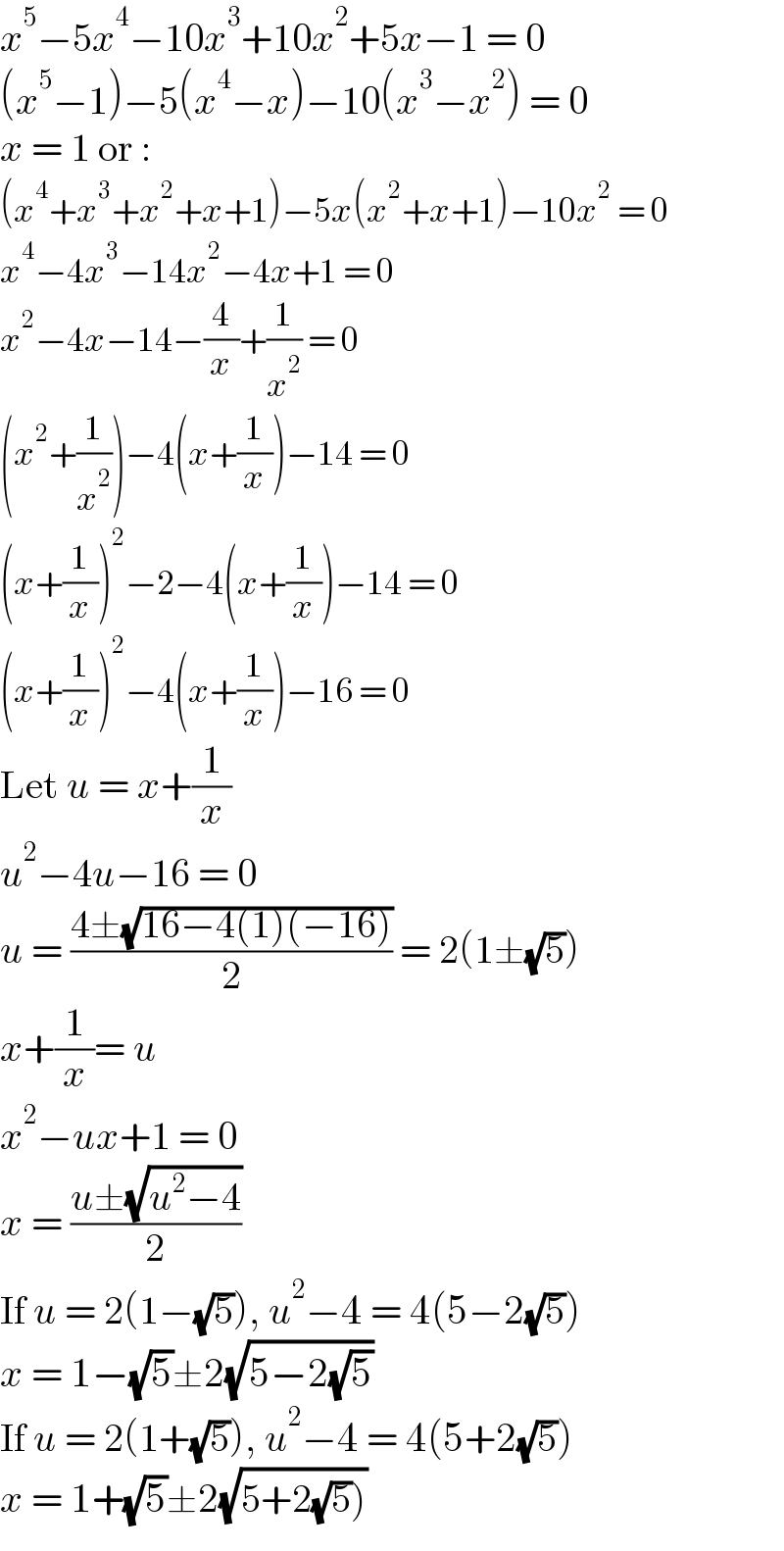
x^5 −5x^4 −10x^3 +10x^2 +5x−1 = 0 (x^5 −1)−5(x^4 −x)−10(x^3 −x^2 ) = 0 x = 1 or : (x^4 +x^3 +x^2 +x+1)−5x(x^2 +x+1)−10x^2 = 0 x^4 −4x^3 −14x^2 −4x+1 = 0 x^2 −4x−14−(4/x)+(1/x^2 ) = 0 (x^2 +(1/x^2 ))−4(x+(1/x))−14 = 0 (x+(1/x))^2 −2−4(x+(1/x))−14 = 0 (x+(1/x))^2 −4(x+(1/x))−16 = 0 Let u = x+(1/x) u^2 −4u−16 = 0 u = ((4±(√(16−4(1)(−16))))/2) = 2(1±(√5)) x+(1/x)= u x^2 −ux+1 = 0 x = ((u±(√(u^2 −4)))/2) If u = 2(1−(√5)), u^2 −4 = 4(5−2(√5)) x = 1−(√5)±2(√(5−2(√5))) If u = 2(1+(√5)), u^2 −4 = 4(5+2(√5)) x = 1+(√5)±2(√(5+2(√5))))

$${x}^{\mathrm{5}} −\mathrm{5}{x}^{\mathrm{4}} −\mathrm{10}{x}^{\mathrm{3}} +\mathrm{10}{x}^{\mathrm{2}} +\mathrm{5}{x}−\mathrm{1}\:=\:\mathrm{0} \\ $$$$\left({x}^{\mathrm{5}} −\mathrm{1}\right)−\mathrm{5}\left({x}^{\mathrm{4}} −{x}\right)−\mathrm{10}\left({x}^{\mathrm{3}} −{x}^{\mathrm{2}} \right)\:=\:\mathrm{0} \\ $$$${x}\:=\:\mathrm{1}\:\mathrm{or}\:: \\ $$$$\left({x}^{\mathrm{4}} +{x}^{\mathrm{3}} +{x}^{\mathrm{2}} +{x}+\mathrm{1}\right)−\mathrm{5}{x}\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right)−\mathrm{10}{x}^{\mathrm{2}} \:=\:\mathrm{0} \\ $$$${x}^{\mathrm{4}} −\mathrm{4}{x}^{\mathrm{3}} −\mathrm{14}{x}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{1}\:=\:\mathrm{0} \\ $$$${x}^{\mathrm{2}} −\mathrm{4}{x}−\mathrm{14}−\frac{\mathrm{4}}{{x}}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\:=\:\mathrm{0} \\ $$$$\left({x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right)−\mathrm{4}\left({x}+\frac{\mathrm{1}}{{x}}\right)−\mathrm{14}\:=\:\mathrm{0} \\ $$$$\left({x}+\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} −\mathrm{2}−\mathrm{4}\left({x}+\frac{\mathrm{1}}{{x}}\right)−\mathrm{14}\:=\:\mathrm{0} \\ $$$$\left({x}+\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} −\mathrm{4}\left({x}+\frac{\mathrm{1}}{{x}}\right)−\mathrm{16}\:=\:\mathrm{0} \\ $$$$\mathrm{Let}\:{u}\:=\:{x}+\frac{\mathrm{1}}{{x}} \\ $$$${u}^{\mathrm{2}} −\mathrm{4}{u}−\mathrm{16}\:=\:\mathrm{0} \\ $$$${u}\:=\:\frac{\mathrm{4}\pm\sqrt{\mathrm{16}−\mathrm{4}\left(\mathrm{1}\right)\left(−\mathrm{16}\right)}}{\mathrm{2}}\:=\:\mathrm{2}\left(\mathrm{1}\pm\sqrt{\mathrm{5}}\right) \\ $$$${x}+\frac{\mathrm{1}}{{x}}=\:{u} \\ $$$${x}^{\mathrm{2}} −{ux}+\mathrm{1}\:=\:\mathrm{0} \\ $$$${x}\:=\:\frac{{u}\pm\sqrt{{u}^{\mathrm{2}} −\mathrm{4}}}{\mathrm{2}} \\ $$$$\mathrm{If}\:{u}\:=\:\mathrm{2}\left(\mathrm{1}−\sqrt{\mathrm{5}}\right),\:{u}^{\mathrm{2}} −\mathrm{4}\:=\:\mathrm{4}\left(\mathrm{5}−\mathrm{2}\sqrt{\mathrm{5}}\right) \\ $$$${x}\:=\:\mathrm{1}−\sqrt{\mathrm{5}}\pm\mathrm{2}\sqrt{\mathrm{5}−\mathrm{2}\sqrt{\mathrm{5}}} \\ $$$$\mathrm{If}\:{u}\:=\:\mathrm{2}\left(\mathrm{1}+\sqrt{\mathrm{5}}\right),\:{u}^{\mathrm{2}} −\mathrm{4}\:=\:\mathrm{4}\left(\mathrm{5}+\mathrm{2}\sqrt{\mathrm{5}}\right) \\ $$$${x}\:=\:\mathrm{1}+\sqrt{\mathrm{5}}\pm\mathrm{2}\sqrt{\left.\mathrm{5}+\mathrm{2}\sqrt{\mathrm{5}}\right)} \\ $$

Commented by mnjuly1970 last updated on 19/Dec/20

$${mercey}\:{mr}\:{olaf}…{thank}\:{you}… \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply