Question Number 126408 by morarupaula last updated on 20/Dec/20

Answered by Dwaipayan Shikari last updated on 20/Dec/20
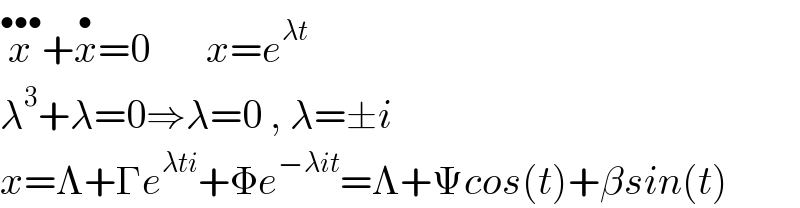
$$\overset{\bullet\bullet\bullet} {{x}}+\overset{\bullet} {{x}}=\mathrm{0}\:\:\:\:\:\:\:{x}={e}^{\lambda{t}} \\ $$$$\lambda^{\mathrm{3}} +\lambda=\mathrm{0}\Rightarrow\lambda=\mathrm{0}\:,\:\lambda=\pm{i} \\ $$$${x}=\Lambda+\Gamma{e}^{\lambda{ti}} +\Phi{e}^{−\lambda{it}} =\Lambda+\Psi{cos}\left({t}\right)+\beta{sin}\left({t}\right) \\ $$
Answered by Olaf last updated on 22/Dec/20

$${x}^{'''} +{x}'\:=\:\mathrm{0} \\ $$$${x}'''{x}''+{x}''{x}'\:=\:\mathrm{0} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}{x}^{''^{\mathrm{2}} } +\frac{\mathrm{1}}{\mathrm{2}}{x}'^{\mathrm{2}} \:=\:\mathrm{C}_{\mathrm{1}} \:\left(\mathrm{C}_{\mathrm{1}} \geqslant\mathrm{0}\right) \\ $$$${x}^{''^{\mathrm{2}} } +{x}'^{\mathrm{2}} \:=\:\mathrm{C}_{\mathrm{2}} \:\left(\mathrm{C}_{\mathrm{2}} \geqslant\mathrm{0}\right) \\ $$$$\frac{{x}''^{\mathrm{2}} }{\:\sqrt{\mathrm{C}_{\mathrm{2}} −{x}'^{\mathrm{2}} }}\:=\:\mathrm{1} \\ $$$$\mathrm{arcsin}\left(\frac{{x}'}{\:\sqrt{\mathrm{C}_{\mathrm{2}} }}\right)\:=\:{t}+\mathrm{C}_{\mathrm{3}} \\ $$$$\mathrm{arcsin}\left(\frac{{x}'}{\:\mathrm{C}_{\mathrm{4}} }\right)\:=\:{t}+\mathrm{C}_{\mathrm{3}} \\ $$$${x}'\:=\:\mathrm{C}_{\mathrm{4}} \mathrm{sin}\left({t}+\mathrm{C}_{\mathrm{3}} \right) \\ $$$${x}\:=\:−\mathrm{C}_{\mathrm{4}} \mathrm{cos}\left({t}+\mathrm{C}_{\mathrm{3}} \right)+\mathrm{C}_{\mathrm{5}} \\ $$$$\mathrm{General}\:\mathrm{solution}\:: \\ $$$${x}\:=\:\alpha\mathrm{cos}\left({t}+\beta\right)+\gamma \\ $$
