Menu Close

Question-126509

Tinku Tara 0 Comments
Pin




Question Number 126509 by Algoritm last updated on 21/Dec/20
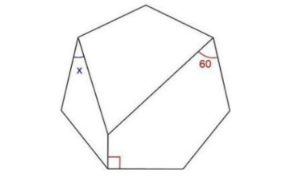
Answered by mr W last updated on 21/Dec/20
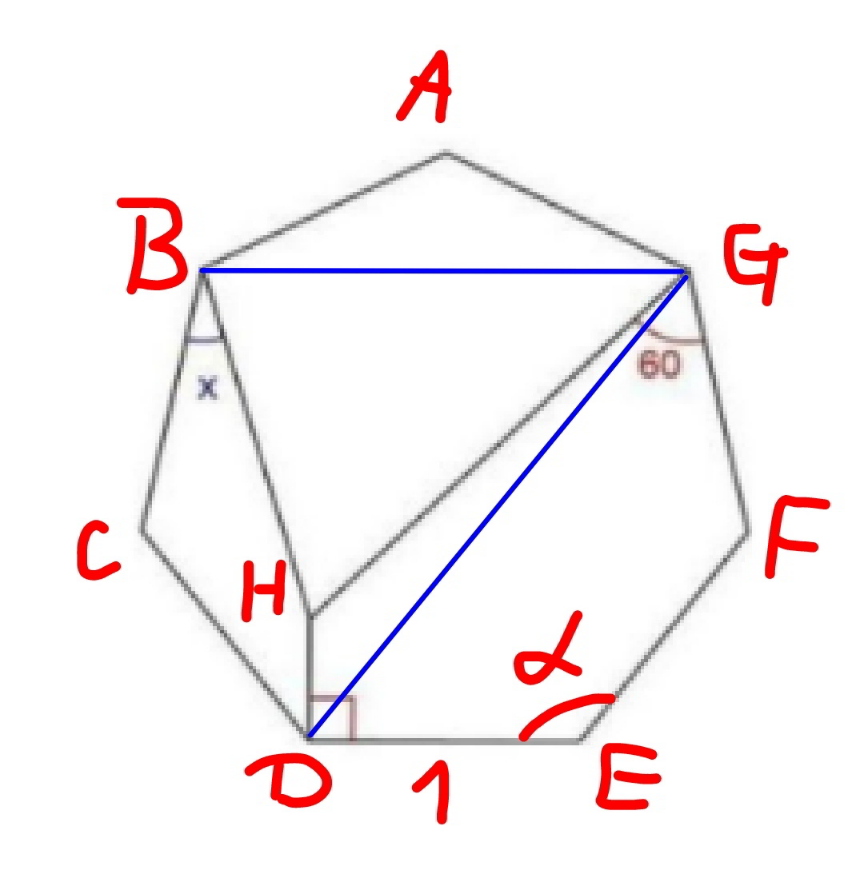
Commented by talminator2856791 last updated on 22/Dec/20
so then the answer?
$$\:\mathrm{so}\:\mathrm{then}\:\mathrm{the}\:\mathrm{answer}? \\ $$
Commented by mr W last updated on 22/Dec/20
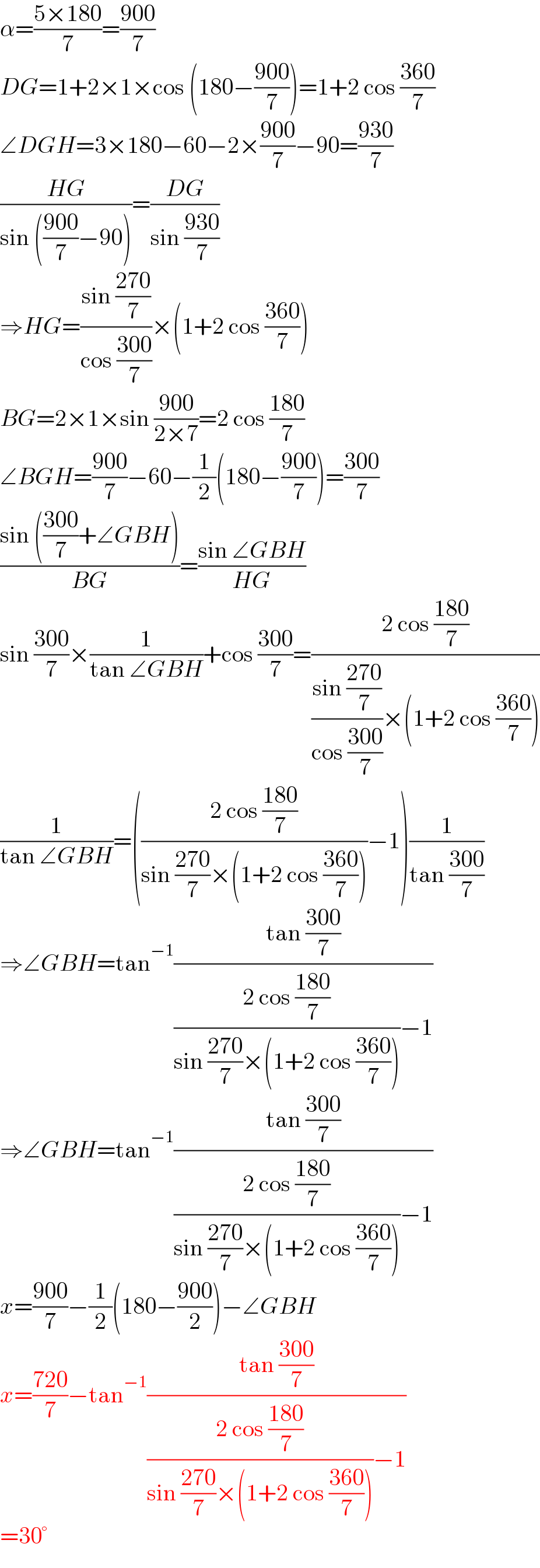
α=((5×180)/7)=((900)/7) DG=1+2×1×cos (180−((900)/7))=1+2 cos ((360)/7) ∠DGH=3×180−60−2×((900)/7)−90=((930)/7) ((HG)/(sin (((900)/7)−90)))=((DG)/(sin ((930)/7))) ⇒HG=((sin ((270)/7))/(cos ((300)/7)))×(1+2 cos ((360)/7)) BG=2×1×sin ((900)/(2×7))=2 cos ((180)/7) ∠BGH=((900)/7)−60−(1/2)(180−((900)/7))=((300)/7) ((sin (((300)/7)+∠GBH))/(BG))=((sin ∠GBH)/(HG)) sin ((300)/7)×(1/(tan ∠GBH))+cos ((300)/7)=((2 cos ((180)/7))/(((sin ((270)/7))/(cos ((300)/7)))×(1+2 cos ((360)/7)))) (1/(tan ∠GBH))=(((2 cos ((180)/7))/(sin ((270)/7)×(1+2 cos ((360)/7))))−1)(1/(tan ((300)/7))) ⇒∠GBH=tan^(−1) ((tan ((300)/7))/(((2 cos ((180)/7))/(sin ((270)/7)×(1+2 cos ((360)/7))))−1)) ⇒∠GBH=tan^(−1) ((tan ((300)/7))/(((2 cos ((180)/7))/(sin ((270)/7)×(1+2 cos ((360)/7))))−1)) x=((900)/7)−(1/2)(180−((900)/2))−∠GBH x=((720)/7)−tan^(−1) ((tan ((300)/7))/(((2 cos ((180)/7))/(sin ((270)/7)×(1+2 cos ((360)/7))))−1)) =30°
$$\alpha=\frac{\mathrm{5}×\mathrm{180}}{\mathrm{7}}=\frac{\mathrm{900}}{\mathrm{7}} \\ $$$${DG}=\mathrm{1}+\mathrm{2}×\mathrm{1}×\mathrm{cos}\:\left(\mathrm{180}−\frac{\mathrm{900}}{\mathrm{7}}\right)=\mathrm{1}+\mathrm{2}\:\mathrm{cos}\:\frac{\mathrm{360}}{\mathrm{7}} \\ $$$$\angle{DGH}=\mathrm{3}×\mathrm{180}−\mathrm{60}−\mathrm{2}×\frac{\mathrm{900}}{\mathrm{7}}−\mathrm{90}=\frac{\mathrm{930}}{\mathrm{7}} \\ $$$$\frac{{HG}}{\mathrm{sin}\:\left(\frac{\mathrm{900}}{\mathrm{7}}−\mathrm{90}\right)}=\frac{{DG}}{\mathrm{sin}\:\frac{\mathrm{930}}{\mathrm{7}}} \\ $$$$\Rightarrow{HG}=\frac{\mathrm{sin}\:\frac{\mathrm{270}}{\mathrm{7}}}{\mathrm{cos}\:\frac{\mathrm{300}}{\mathrm{7}}}×\left(\mathrm{1}+\mathrm{2}\:\mathrm{cos}\:\frac{\mathrm{360}}{\mathrm{7}}\right) \\ $$$${BG}=\mathrm{2}×\mathrm{1}×\mathrm{sin}\:\frac{\mathrm{900}}{\mathrm{2}×\mathrm{7}}=\mathrm{2}\:\mathrm{cos}\:\frac{\mathrm{180}}{\mathrm{7}} \\ $$$$\angle{BGH}=\frac{\mathrm{900}}{\mathrm{7}}−\mathrm{60}−\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{180}−\frac{\mathrm{900}}{\mathrm{7}}\right)=\frac{\mathrm{300}}{\mathrm{7}} \\ $$$$\frac{\mathrm{sin}\:\left(\frac{\mathrm{300}}{\mathrm{7}}+\angle{GBH}\right)}{{BG}}=\frac{\mathrm{sin}\:\angle{GBH}}{{HG}} \\ $$$$\mathrm{sin}\:\frac{\mathrm{300}}{\mathrm{7}}×\frac{\mathrm{1}}{\mathrm{tan}\:\angle{GBH}}+\mathrm{cos}\:\frac{\mathrm{300}}{\mathrm{7}}=\frac{\mathrm{2}\:\mathrm{cos}\:\frac{\mathrm{180}}{\mathrm{7}}}{\frac{\mathrm{sin}\:\frac{\mathrm{270}}{\mathrm{7}}}{\mathrm{cos}\:\frac{\mathrm{300}}{\mathrm{7}}}×\left(\mathrm{1}+\mathrm{2}\:\mathrm{cos}\:\frac{\mathrm{360}}{\mathrm{7}}\right)} \\ $$$$\frac{\mathrm{1}}{\mathrm{tan}\:\angle{GBH}}=\left(\frac{\mathrm{2}\:\mathrm{cos}\:\frac{\mathrm{180}}{\mathrm{7}}}{\mathrm{sin}\:\frac{\mathrm{270}}{\mathrm{7}}×\left(\mathrm{1}+\mathrm{2}\:\mathrm{cos}\:\frac{\mathrm{360}}{\mathrm{7}}\right)}−\mathrm{1}\right)\frac{\mathrm{1}}{\mathrm{tan}\:\frac{\mathrm{300}}{\mathrm{7}}} \\ $$$$\Rightarrow\angle{GBH}=\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{tan}\:\frac{\mathrm{300}}{\mathrm{7}}}{\frac{\mathrm{2}\:\mathrm{cos}\:\frac{\mathrm{180}}{\mathrm{7}}}{\mathrm{sin}\:\frac{\mathrm{270}}{\mathrm{7}}×\left(\mathrm{1}+\mathrm{2}\:\mathrm{cos}\:\frac{\mathrm{360}}{\mathrm{7}}\right)}−\mathrm{1}} \\ $$$$\Rightarrow\angle{GBH}=\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{tan}\:\frac{\mathrm{300}}{\mathrm{7}}}{\frac{\mathrm{2}\:\mathrm{cos}\:\frac{\mathrm{180}}{\mathrm{7}}}{\mathrm{sin}\:\frac{\mathrm{270}}{\mathrm{7}}×\left(\mathrm{1}+\mathrm{2}\:\mathrm{cos}\:\frac{\mathrm{360}}{\mathrm{7}}\right)}−\mathrm{1}} \\ $$$${x}=\frac{\mathrm{900}}{\mathrm{7}}−\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{180}−\frac{\mathrm{900}}{\mathrm{2}}\right)−\angle{GBH} \\ $$$${x}=\frac{\mathrm{720}}{\mathrm{7}}−\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{tan}\:\frac{\mathrm{300}}{\mathrm{7}}}{\frac{\mathrm{2}\:\mathrm{cos}\:\frac{\mathrm{180}}{\mathrm{7}}}{\mathrm{sin}\:\frac{\mathrm{270}}{\mathrm{7}}×\left(\mathrm{1}+\mathrm{2}\:\mathrm{cos}\:\frac{\mathrm{360}}{\mathrm{7}}\right)}−\mathrm{1}} \\ $$$$=\mathrm{30}° \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *