Question Number 126567 by sdfg last updated on 21/Dec/20
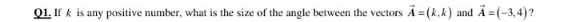
Answered by physicstutes last updated on 22/Dec/20
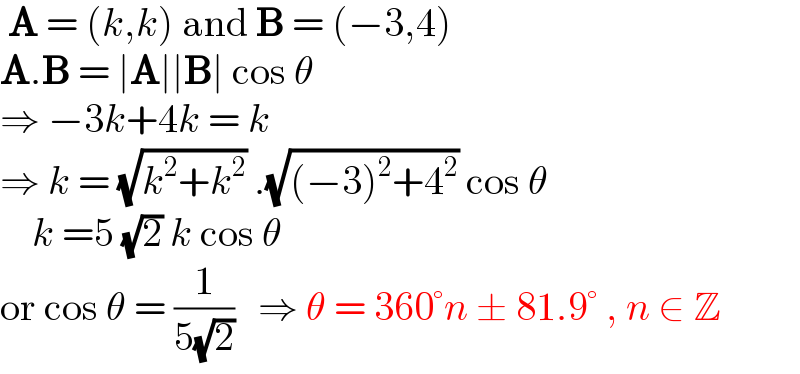
$$\:\boldsymbol{\mathrm{A}}\:=\:\left({k},{k}\right)\:\mathrm{and}\:\boldsymbol{\mathrm{B}}\:=\:\left(−\mathrm{3},\mathrm{4}\right) \\ $$$$\boldsymbol{\mathrm{A}}.\boldsymbol{\mathrm{B}}\:=\:\mid\boldsymbol{\mathrm{A}}\mid\mid\boldsymbol{\mathrm{B}}\mid\:\mathrm{cos}\:\theta \\ $$$$\Rightarrow\:−\mathrm{3}{k}+\mathrm{4}{k}\:=\:{k} \\ $$$$\Rightarrow\:{k}\:=\:\sqrt{{k}^{\mathrm{2}} +{k}^{\mathrm{2}} }\:.\sqrt{\left(−\mathrm{3}\right)^{\mathrm{2}} +\mathrm{4}^{\mathrm{2}} }\:\mathrm{cos}\:\theta \\ $$$$\:\:\:\:{k}\:=\mathrm{5}\:\sqrt{\mathrm{2}}\:{k}\:\mathrm{cos}\:\theta \\ $$$$\mathrm{or}\:\mathrm{cos}\:\theta\:=\:\frac{\mathrm{1}}{\mathrm{5}\sqrt{\mathrm{2}}}\:\:\:\Rightarrow\:\theta\:=\:\mathrm{360}°{n}\:\pm\:\mathrm{81}.\mathrm{9}°\:,\:{n}\:\in\:\mathbb{Z} \\ $$
