Question Number 126632 by BHOOPENDRA last updated on 22/Dec/20
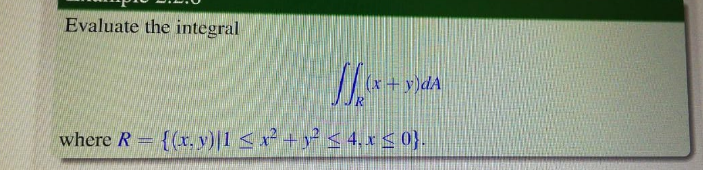
Commented by BHOOPENDRA last updated on 22/Dec/20

$${thanku}\:{sir} \\ $$
Answered by Ar Brandon last updated on 22/Dec/20
![In polar coordinates; { ((x=rcosθ),(r≥0)),((y=rsinθ),(θ∈[0,2π])) :} 1≤x^2 +y^2 ≤4 ⇒ 1≤r^2 ≤4 ⇒ 1≤r≤2 x≤0 ⇒ rcosθ≤0 ⇒ cosθ≤0 ⇒ θ∈[(π/2),((3π)/2)] I=∫∫_R (x+y)dA =∫_((3π)/2) ^(π/2) ∫_1 ^2 r(rcosθ+rsinθ)drdθ =∫_((3π)/2) ^(π/2) ∫_1 ^2 r^2 (cosθ+sinθ)drdθ =[(r^3 /3)]_1 ^2 [sinθ−cosθ]_((3π)/2) ^(π/2) =((8/3)−(1/3))(1−−1)=((14)/3)](https://www.tinkutara.com/question/Q126637.png)
$$\mathrm{In}\:\mathrm{polar}\:\mathrm{coordinates}; \\ $$$$\begin{cases}{\mathrm{x}=\mathrm{rcos}\theta}&{\mathrm{r}\geqslant\mathrm{0}}\\{\mathrm{y}=\mathrm{rsin}\theta}&{\theta\in\left[\mathrm{0},\mathrm{2}\pi\right]}\end{cases} \\ $$$$\mathrm{1}\leqslant\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} \leqslant\mathrm{4}\:\Rightarrow\:\mathrm{1}\leqslant\mathrm{r}^{\mathrm{2}} \leqslant\mathrm{4}\:\Rightarrow\:\mathrm{1}\leqslant\mathrm{r}\leqslant\mathrm{2} \\ $$$$\mathrm{x}\leqslant\mathrm{0}\:\Rightarrow\:\mathrm{rcos}\theta\leqslant\mathrm{0}\:\Rightarrow\:\mathrm{cos}\theta\leqslant\mathrm{0}\:\Rightarrow\:\theta\in\left[\frac{\pi}{\mathrm{2}},\frac{\mathrm{3}\pi}{\mathrm{2}}\right] \\ $$$$\mathcal{I}=\int\int_{\mathbb{R}} \left(\mathrm{x}+\mathrm{y}\right)\mathrm{dA} \\ $$$$\:\:\:=\int_{\frac{\mathrm{3}\pi}{\mathrm{2}}} ^{\frac{\pi}{\mathrm{2}}} \int_{\mathrm{1}} ^{\mathrm{2}} \mathrm{r}\left(\mathrm{rcos}\theta+\mathrm{rsin}\theta\right)\mathrm{drd}\theta \\ $$$$\:\:\:=\int_{\frac{\mathrm{3}\pi}{\mathrm{2}}} ^{\frac{\pi}{\mathrm{2}}} \int_{\mathrm{1}} ^{\mathrm{2}} \mathrm{r}^{\mathrm{2}} \left(\mathrm{cos}\theta+\mathrm{sin}\theta\right)\mathrm{drd}\theta \\ $$$$\:\:\:=\left[\frac{\mathrm{r}^{\mathrm{3}} }{\mathrm{3}}\right]_{\mathrm{1}} ^{\mathrm{2}} \left[\mathrm{sin}\theta−\mathrm{cos}\theta\right]_{\frac{\mathrm{3}\pi}{\mathrm{2}}} ^{\frac{\pi}{\mathrm{2}}} \\ $$$$\:\:\:=\left(\frac{\mathrm{8}}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{3}}\right)\left(\mathrm{1}−−\mathrm{1}\right)=\frac{\mathrm{14}}{\mathrm{3}} \\ $$
Answered by mathmax by abdo last updated on 22/Dec/20
![A =∫∫_R (x+y)dxdy with R ={(x,y)/1≤x^2 +y^2 ≤4 and x≤0} we use the diffeomorphism { ((x=rcosθ)),((y=rsinθ)) :} 1≤x^2 +y^2 ≤4 ⇒1≤r^2 ≤4 ⇒1≤r≤2 x≤0 ⇒cosθ ≤0 ⇒θ ∈[(π/2),((3π)/2)] ⇒ A =∫_1 ^2 ∫_(π/2) ^((3π)/2) (rcosθ +rsinθ)rdrdθ =∫_1 ^2 r^2 dr ∫_(π/2) ^((3π)/2) (cosθ +sinθ)dθ =[(r^3 /3)]_1 ^2 ×[sinθ −cosθ]_(π/2) ^((3π)/2) =(1/3)(8−1)(sin(((3π)/2))−cos(((3π)/2))−sin((π/2))+cos((π/2))) =(7/3)(−1−o−1)=−((14)/3)](https://www.tinkutara.com/question/Q126651.png)
$$\mathrm{A}\:=\int\int_{\mathrm{R}} \left(\mathrm{x}+\mathrm{y}\right)\mathrm{dxdy}\:\:\:\mathrm{with}\:\mathrm{R}\:=\left\{\left(\mathrm{x},\mathrm{y}\right)/\mathrm{1}\leqslant\mathrm{x}^{\mathrm{2}} \:+\mathrm{y}^{\mathrm{2}} \:\leqslant\mathrm{4}\:\mathrm{and}\:\mathrm{x}\leqslant\mathrm{0}\right\} \\ $$$$\mathrm{we}\:\mathrm{use}\:\mathrm{the}\:\mathrm{diffeomorphism}\:\begin{cases}{\mathrm{x}=\mathrm{rcos}\theta}\\{\mathrm{y}=\mathrm{rsin}\theta}\end{cases} \\ $$$$\mathrm{1}\leqslant\mathrm{x}^{\mathrm{2}} \:+\mathrm{y}^{\mathrm{2}} \leqslant\mathrm{4}\:\Rightarrow\mathrm{1}\leqslant\mathrm{r}^{\mathrm{2}} \:\leqslant\mathrm{4}\:\Rightarrow\mathrm{1}\leqslant\mathrm{r}\leqslant\mathrm{2} \\ $$$$\mathrm{x}\leqslant\mathrm{0}\:\Rightarrow\mathrm{cos}\theta\:\leqslant\mathrm{0}\:\Rightarrow\theta\:\in\left[\frac{\pi}{\mathrm{2}},\frac{\mathrm{3}\pi}{\mathrm{2}}\right]\:\Rightarrow \\ $$$$\mathrm{A}\:=\int_{\mathrm{1}} ^{\mathrm{2}} \:\:\int_{\frac{\pi}{\mathrm{2}}} ^{\frac{\mathrm{3}\pi}{\mathrm{2}}} \left(\mathrm{rcos}\theta\:+\mathrm{rsin}\theta\right)\mathrm{rdrd}\theta\:=\int_{\mathrm{1}} ^{\mathrm{2}} \:\mathrm{r}^{\mathrm{2}} \:\mathrm{dr}\:\int_{\frac{\pi}{\mathrm{2}}} ^{\frac{\mathrm{3}\pi}{\mathrm{2}}} \left(\mathrm{cos}\theta\:+\mathrm{sin}\theta\right)\mathrm{d}\theta \\ $$$$=\left[\frac{\mathrm{r}^{\mathrm{3}} }{\mathrm{3}}\right]_{\mathrm{1}} ^{\mathrm{2}} \:×\left[\mathrm{sin}\theta\:−\mathrm{cos}\theta\right]_{\frac{\pi}{\mathrm{2}}} ^{\frac{\mathrm{3}\pi}{\mathrm{2}}} \:=\frac{\mathrm{1}}{\mathrm{3}}\left(\mathrm{8}−\mathrm{1}\right)\left(\mathrm{sin}\left(\frac{\mathrm{3}\pi}{\mathrm{2}}\right)−\mathrm{cos}\left(\frac{\mathrm{3}\pi}{\mathrm{2}}\right)−\mathrm{sin}\left(\frac{\pi}{\mathrm{2}}\right)+\mathrm{cos}\left(\frac{\pi}{\mathrm{2}}\right)\right) \\ $$$$=\frac{\mathrm{7}}{\mathrm{3}}\left(−\mathrm{1}−\mathrm{o}−\mathrm{1}\right)=−\frac{\mathrm{14}}{\mathrm{3}} \\ $$
