Question Number 126635 by BHOOPENDRA last updated on 22/Dec/20
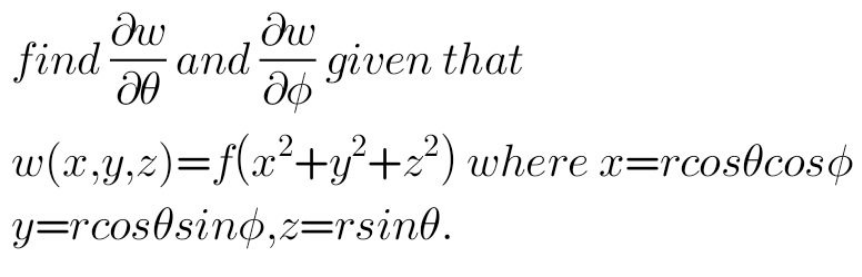
Answered by Ar Brandon last updated on 22/Dec/20
![x^2 +y^2 +z^2 =r^2 cos^2 θcos^2 φ+r^2 cos^2 θsin^2 φ+r^2 sinθ =r^2 [cos^2 θ(cos^2 φ+sin^2 φ)_(1) +sin^2 θ] =r^2 [cos^2 θ+sin^2 θ]=r^2 w(x,y,z)=f(x^2 +y^2 +z^2 )=f(r^2 ) (∂w/∂θ)=((∂f(r^2 ))/∂θ)=0=(∂w/∂φ)](https://www.tinkutara.com/question/Q126639.png)
$$\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} +\mathrm{z}^{\mathrm{2}} =\mathrm{r}^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \theta\mathrm{cos}^{\mathrm{2}} \phi+\mathrm{r}^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \theta\mathrm{sin}^{\mathrm{2}} \phi+\mathrm{r}^{\mathrm{2}} \mathrm{sin}\theta \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{r}^{\mathrm{2}} \left[\mathrm{cos}^{\mathrm{2}} \theta\underset{\mathrm{1}} {\underbrace{\left(\mathrm{cos}^{\mathrm{2}} \phi+\mathrm{sin}^{\mathrm{2}} \phi\right)}}+\mathrm{sin}^{\mathrm{2}} \theta\right] \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{r}^{\mathrm{2}} \left[\mathrm{cos}^{\mathrm{2}} \theta+\mathrm{sin}^{\mathrm{2}} \theta\right]=\mathrm{r}^{\mathrm{2}} \\ $$$${w}\left({x},{y},{z}\right)={f}\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{z}^{\mathrm{2}} \right)={f}\left({r}^{\mathrm{2}} \right) \\ $$$$\frac{\partial{w}}{\partial\theta}=\frac{\partial{f}\left({r}^{\mathrm{2}} \right)}{\partial\theta}=\mathrm{0}=\frac{\partial{w}}{\partial\phi} \\ $$
