Question-126641

Question Number 126641 by TITA last updated on 22/Dec/20

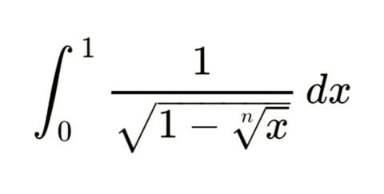
Commented by TITA last updated on 22/Dec/20

$$\mathrm{please}\:\mathrm{help} \\ $$

Answered by Lordose last updated on 22/Dec/20

Ω = ∫_0 ^( 1) (1/( (√(1−(x)^(1/n) ))))dx =^(x = u^n ) n∫_0 ^( 1) u^(n−1) (1−u)^(−(1/2)) du Ω = nB(n,(1/2)) = ((n𝚪(n)𝚪((1/2)))/(𝚪(n + (1/2)))) = ((n𝚪(n)(√𝛑))/(𝚪(n + (1/2))))

$$ \\ $$$$\Omega\:=\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\mathrm{1}}{\:\sqrt{\mathrm{1}−\sqrt[{\mathrm{n}}]{\mathrm{x}}}}\mathrm{dx}\:\overset{\mathrm{x}\:=\:\mathrm{u}^{\mathrm{n}} } {=}\mathrm{n}\int_{\mathrm{0}} ^{\:\mathrm{1}} \mathrm{u}^{\mathrm{n}−\mathrm{1}} \left(\mathrm{1}−\mathrm{u}\right)^{−\frac{\mathrm{1}}{\mathrm{2}}} \mathrm{du}\: \\ $$$$\Omega\:=\:\boldsymbol{\mathrm{nB}}\left(\mathrm{n},\frac{\mathrm{1}}{\mathrm{2}}\right)\:=\:\frac{\boldsymbol{\mathrm{n}\Gamma}\left(\boldsymbol{\mathrm{n}}\right)\boldsymbol{\Gamma}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)}{\boldsymbol{\Gamma}\left(\boldsymbol{\mathrm{n}}\:+\:\frac{\mathrm{1}}{\mathrm{2}}\right)}\:=\:\frac{\boldsymbol{\mathrm{n}\Gamma}\left(\boldsymbol{\mathrm{n}}\right)\sqrt{\boldsymbol{\pi}}}{\boldsymbol{\Gamma}\left(\boldsymbol{\mathrm{n}}\:+\:\frac{\mathrm{1}}{\mathrm{2}}\right)} \\ $$

Commented by TITA last updated on 22/Dec/20

$$\mathrm{thanks} \\ $$

Answered by Dwaipayan Shikari last updated on 23/Dec/20

x=sin^(2n) θ⇒1=2nsin^(2n−1) θ cosθ(dθ/dx) =∫_0 ^1 (1/( (√(1−(x)^(1/n) ))))dx=2n∫_0 ^(π/2) ((sin^(2n−1) θcosθ)/( (√(1−sin^2 θ))))dθ =2n∫_0 ^(π/2) sin^(2n−1) cos^(2((1/2))−1) θdθ=n((Γ(n)Γ((1/2)))/(Γ(n+(1/2))))=n(√π).((Γ(n))/(Γ(n+(1/2)))) =((Γ(n+1)(√π))/(Γ(n+(1/2))))

$${x}={sin}^{\mathrm{2}{n}} \theta\Rightarrow\mathrm{1}=\mathrm{2}{nsin}^{\mathrm{2}{n}−\mathrm{1}} \theta\:{cos}\theta\frac{{d}\theta}{{dx}}\: \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{\:\sqrt{\mathrm{1}−\sqrt[{{n}}]{{x}}}}{dx}=\mathrm{2}{n}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{sin}^{\mathrm{2}{n}−\mathrm{1}} \theta{cos}\theta}{\:\sqrt{\mathrm{1}−{sin}^{\mathrm{2}} \theta}}{d}\theta \\ $$$$=\mathrm{2}{n}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {sin}^{\mathrm{2}{n}−\mathrm{1}} {cos}^{\mathrm{2}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)−\mathrm{1}} \theta{d}\theta={n}\frac{\Gamma\left({n}\right)\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right)}{\Gamma\left({n}+\frac{\mathrm{1}}{\mathrm{2}}\right)}={n}\sqrt{\pi}.\frac{\Gamma\left({n}\right)}{\Gamma\left({n}+\frac{\mathrm{1}}{\mathrm{2}}\right)} \\ $$$$=\frac{\Gamma\left({n}+\mathrm{1}\right)\sqrt{\pi}}{\Gamma\left({n}+\frac{\mathrm{1}}{\mathrm{2}}\right)} \\ $$

Answered by mathmax by abdo last updated on 22/Dec/20

A =∫_0 ^1 (dx/( (√(1−x^(1/n) )))) changement x^(1/n) =t give x=t^n ⇒ A =∫_0 ^1 ((nt^(n−1) dt)/( (√(1−t))))=n ∫_0 ^1 t^(n−1) (1−t)^(−(1/2)) dt =n∫_0 ^1 t^(n−1) (1−t)^((1/2)−1) dt =nB(n,(1/2))=n.((Γ(n)Γ((1/2)))/(Γ(n+(1/2)))) =((n(n−1)!(√π))/(Γ(n+(1/2)))) (n≥1)

$$\mathrm{A}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{dx}}{\:\sqrt{\mathrm{1}−\mathrm{x}^{\frac{\mathrm{1}}{\mathrm{n}}} }}\:\mathrm{changement}\:\mathrm{x}^{\frac{\mathrm{1}}{\mathrm{n}}} =\mathrm{t}\:\mathrm{give}\:\mathrm{x}=\mathrm{t}^{\mathrm{n}} \:\Rightarrow \\ $$$$\mathrm{A}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{nt}^{\mathrm{n}−\mathrm{1}} \mathrm{dt}}{\:\sqrt{\mathrm{1}−\mathrm{t}}}=\mathrm{n}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{t}^{\mathrm{n}−\mathrm{1}} \:\left(\mathrm{1}−\mathrm{t}\right)^{−\frac{\mathrm{1}}{\mathrm{2}}} \:\mathrm{dt}\:=\mathrm{n}\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{t}^{\mathrm{n}−\mathrm{1}} \left(\mathrm{1}−\mathrm{t}\right)^{\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{1}} \:\mathrm{dt} \\ $$$$=\mathrm{nB}\left(\mathrm{n},\frac{\mathrm{1}}{\mathrm{2}}\right)=\mathrm{n}.\frac{\Gamma\left(\mathrm{n}\right)\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right)}{\Gamma\left(\mathrm{n}+\frac{\mathrm{1}}{\mathrm{2}}\right)}\:=\frac{\mathrm{n}\left(\mathrm{n}−\mathrm{1}\right)!\sqrt{\pi}}{\Gamma\left(\mathrm{n}+\frac{\mathrm{1}}{\mathrm{2}}\right)}\:\:\:\left(\mathrm{n}\geqslant\mathrm{1}\right) \\ $$

Answered by Olaf last updated on 22/Dec/20

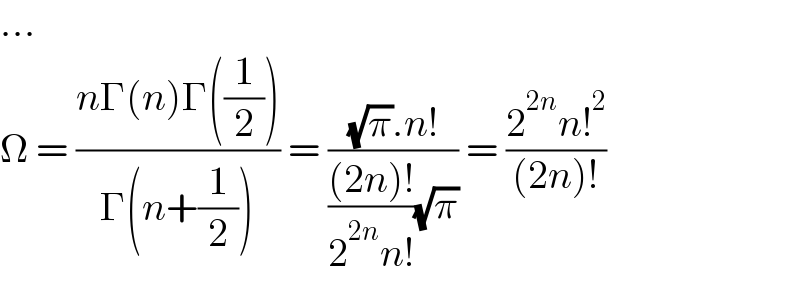
... Ω = ((nΓ(n)Γ((1/2)))/(Γ(n+(1/2)))) = (((√π).n!)/((((2n)!)/(2^(2n) n!))(√π))) = ((2^(2n) n!^2 )/((2n)!))

$$… \\ $$$$\Omega\:=\:\frac{{n}\Gamma\left({n}\right)\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right)}{\Gamma\left({n}+\frac{\mathrm{1}}{\mathrm{2}}\right)}\:=\:\frac{\sqrt{\pi}.{n}!}{\frac{\left(\mathrm{2}{n}\right)!}{\mathrm{2}^{\mathrm{2}{n}} {n}!}\sqrt{\pi}}\:=\:\frac{\mathrm{2}^{\mathrm{2}{n}} {n}!^{\mathrm{2}} }{\left(\mathrm{2}{n}\right)!} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply