Question Number 126657 by adeyemiprof40 last updated on 23/Dec/20

Answered by Olaf last updated on 23/Dec/20
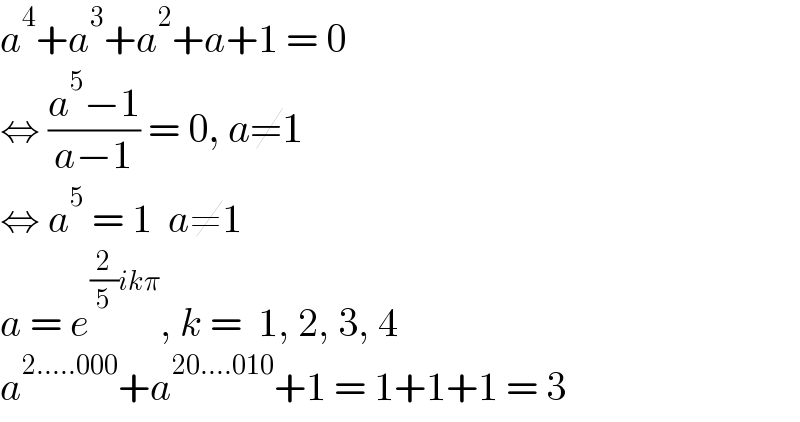
$${a}^{\mathrm{4}} +{a}^{\mathrm{3}} +{a}^{\mathrm{2}} +{a}+\mathrm{1}\:=\:\mathrm{0} \\ $$$$\Leftrightarrow\:\frac{{a}^{\mathrm{5}} −\mathrm{1}}{{a}−\mathrm{1}}\:=\:\mathrm{0},\:{a}\neq\mathrm{1} \\ $$$$\Leftrightarrow\:{a}^{\mathrm{5}} \:=\:\mathrm{1}\:\:{a}\neq\mathrm{1} \\ $$$${a}\:=\:{e}^{\frac{\mathrm{2}}{\mathrm{5}}{ik}\pi} ,\:{k}\:=\:\:\mathrm{1},\:\mathrm{2},\:\mathrm{3},\:\mathrm{4} \\ $$$${a}^{\mathrm{2}…..\mathrm{000}} +{a}^{\mathrm{20}….\mathrm{010}} +\mathrm{1}\:=\:\mathrm{1}+\mathrm{1}+\mathrm{1}\:=\:\mathrm{3} \\ $$
Answered by AlagaIbile last updated on 23/Dec/20
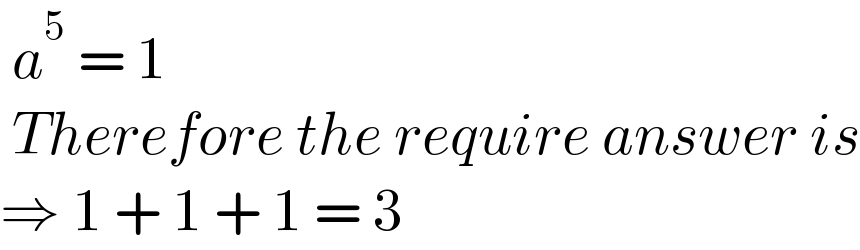
$$\:{a}^{\mathrm{5}} \:=\:\mathrm{1} \\ $$$$\:{Therefore}\:{the}\:{require}\:{answer}\:{is} \\ $$$$\Rightarrow\:\mathrm{1}\:+\:\mathrm{1}\:+\:\mathrm{1}\:=\:\mathrm{3} \\ $$
