Menu Close

Question-126677

Tinku Tara 0 Comments
Pin




Question Number 126677 by AST last updated on 26/Sep/22
Commented by talminator2856791 last updated on 23/Dec/20
what is the question?
$$\:\mathrm{what}\:\mathrm{is}\:\mathrm{the}\:\mathrm{question}? \\ $$$$\: \\ $$
Commented by talminator2856791 last updated on 23/Dec/20
what is mod in this context
$$\:\mathrm{what}\:\mathrm{is}\:\mathrm{mod}\:\mathrm{in}\:\mathrm{this}\:\mathrm{context} \\ $$
Commented by talminator2856791 last updated on 23/Dec/20
ooooooooooh
$$\: \\ $$$$\:\mathrm{ooooooooooh} \\ $$
Answered by floor(10²Eta[1]) last updated on 24/Dec/20
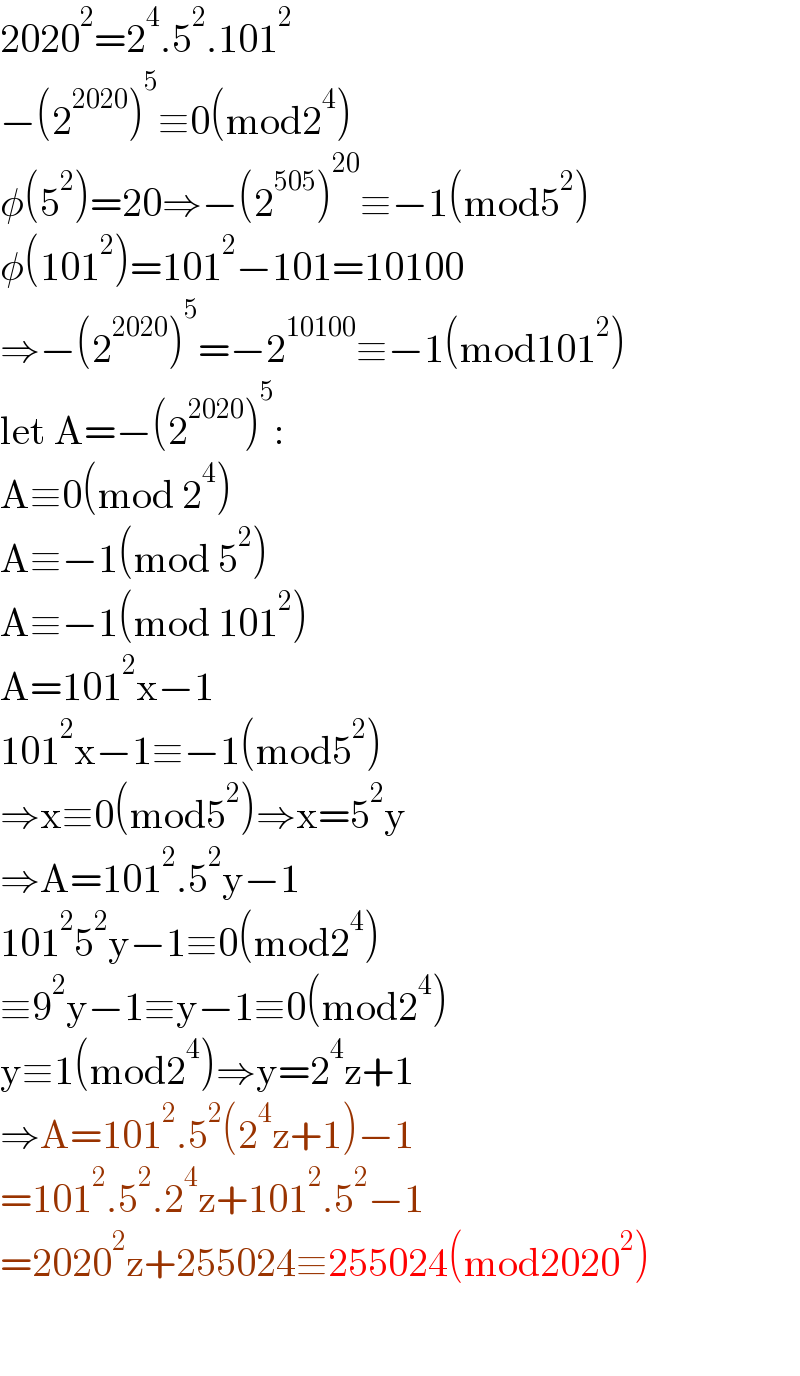
2020^2 =2^4 .5^2 .101^2 −(2^(2020) )^5 ≡0(mod2^4 ) φ(5^2 )=20⇒−(2^(505) )^(20) ≡−1(mod5^2 ) φ(101^2 )=101^2 −101=10100 ⇒−(2^(2020) )^5 =−2^(10100) ≡−1(mod101^2 ) let A=−(2^(2020) )^5 : A≡0(mod 2^4 ) A≡−1(mod 5^2 ) A≡−1(mod 101^2 ) A=101^2 x−1 101^2 x−1≡−1(mod5^2 ) ⇒x≡0(mod5^2 )⇒x=5^2 y ⇒A=101^2 .5^2 y−1 101^2 5^2 y−1≡0(mod2^4 ) ≡9^2 y−1≡y−1≡0(mod2^4 ) y≡1(mod2^4 )⇒y=2^4 z+1 ⇒A=101^2 .5^2 (2^4 z+1)−1 =101^2 .5^2 .2^4 z+101^2 .5^2 −1 =2020^2 z+255024≡255024(mod2020^2 )
$$\mathrm{2020}^{\mathrm{2}} =\mathrm{2}^{\mathrm{4}} .\mathrm{5}^{\mathrm{2}} .\mathrm{101}^{\mathrm{2}} \\ $$$$−\left(\mathrm{2}^{\mathrm{2020}} \right)^{\mathrm{5}} \equiv\mathrm{0}\left(\mathrm{mod2}^{\mathrm{4}} \right) \\ $$$$\phi\left(\mathrm{5}^{\mathrm{2}} \right)=\mathrm{20}\Rightarrow−\left(\mathrm{2}^{\mathrm{505}} \right)^{\mathrm{20}} \equiv−\mathrm{1}\left(\mathrm{mod5}^{\mathrm{2}} \right) \\ $$$$\phi\left(\mathrm{101}^{\mathrm{2}} \right)=\mathrm{101}^{\mathrm{2}} −\mathrm{101}=\mathrm{10100} \\ $$$$\Rightarrow−\left(\mathrm{2}^{\mathrm{2020}} \right)^{\mathrm{5}} =−\mathrm{2}^{\mathrm{10100}} \equiv−\mathrm{1}\left(\mathrm{mod101}^{\mathrm{2}} \right) \\ $$$$\mathrm{let}\:\mathrm{A}=−\left(\mathrm{2}^{\mathrm{2020}} \right)^{\mathrm{5}} : \\ $$$$\mathrm{A}\equiv\mathrm{0}\left(\mathrm{mod}\:\mathrm{2}^{\mathrm{4}} \right) \\ $$$$\mathrm{A}\equiv−\mathrm{1}\left(\mathrm{mod}\:\mathrm{5}^{\mathrm{2}} \right) \\ $$$$\mathrm{A}\equiv−\mathrm{1}\left(\mathrm{mod}\:\mathrm{101}^{\mathrm{2}} \right) \\ $$$$\mathrm{A}=\mathrm{101}^{\mathrm{2}} \mathrm{x}−\mathrm{1} \\ $$$$\mathrm{101}^{\mathrm{2}} \mathrm{x}−\mathrm{1}\equiv−\mathrm{1}\left(\mathrm{mod5}^{\mathrm{2}} \right) \\ $$$$\Rightarrow\mathrm{x}\equiv\mathrm{0}\left(\mathrm{mod5}^{\mathrm{2}} \right)\Rightarrow\mathrm{x}=\mathrm{5}^{\mathrm{2}} \mathrm{y} \\ $$$$\Rightarrow\mathrm{A}=\mathrm{101}^{\mathrm{2}} .\mathrm{5}^{\mathrm{2}} \mathrm{y}−\mathrm{1} \\ $$$$\mathrm{101}^{\mathrm{2}} \mathrm{5}^{\mathrm{2}} \mathrm{y}−\mathrm{1}\equiv\mathrm{0}\left(\mathrm{mod2}^{\mathrm{4}} \right) \\ $$$$\equiv\mathrm{9}^{\mathrm{2}} \mathrm{y}−\mathrm{1}\equiv\mathrm{y}−\mathrm{1}\equiv\mathrm{0}\left(\mathrm{mod2}^{\mathrm{4}} \right) \\ $$$$\mathrm{y}\equiv\mathrm{1}\left(\mathrm{mod2}^{\mathrm{4}} \right)\Rightarrow\mathrm{y}=\mathrm{2}^{\mathrm{4}} \mathrm{z}+\mathrm{1} \\ $$$$\Rightarrow\mathrm{A}=\mathrm{101}^{\mathrm{2}} .\mathrm{5}^{\mathrm{2}} \left(\mathrm{2}^{\mathrm{4}} \mathrm{z}+\mathrm{1}\right)−\mathrm{1} \\ $$$$=\mathrm{101}^{\mathrm{2}} .\mathrm{5}^{\mathrm{2}} .\mathrm{2}^{\mathrm{4}} \mathrm{z}+\mathrm{101}^{\mathrm{2}} .\mathrm{5}^{\mathrm{2}} −\mathrm{1} \\ $$$$=\mathrm{2020}^{\mathrm{2}} \mathrm{z}+\mathrm{255024}\equiv\mathrm{255024}\left(\mathrm{mod2020}^{\mathrm{2}} \right) \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *