Question Number 126712 by help last updated on 23/Dec/20

Commented by liberty last updated on 24/Dec/20
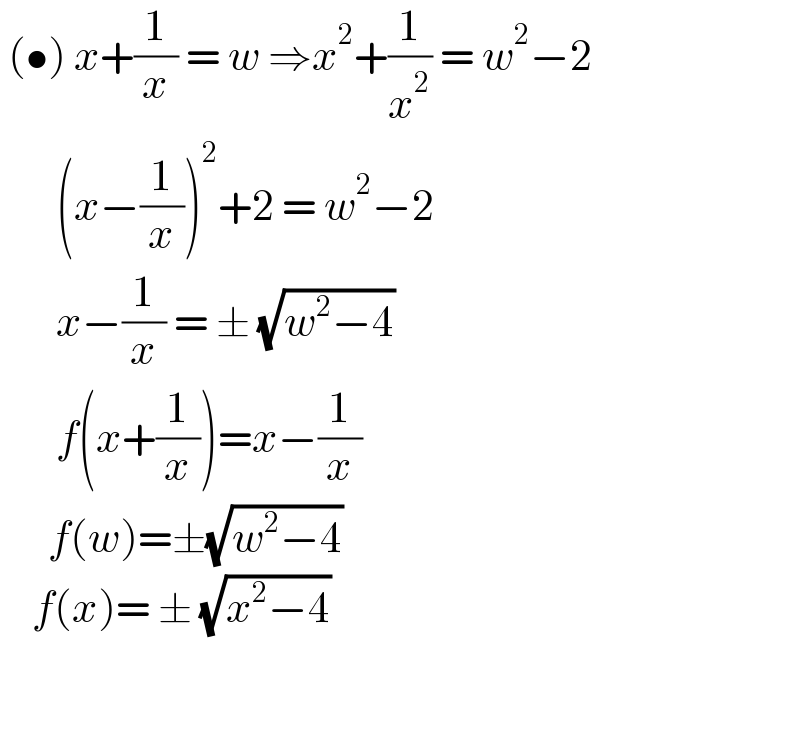
$$\:\left(\bullet\right)\:{x}+\frac{\mathrm{1}}{{x}}\:=\:{w}\:\Rightarrow{x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\:=\:{w}^{\mathrm{2}} −\mathrm{2} \\ $$$$\:\:\:\:\:\:\:\left({x}−\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} +\mathrm{2}\:=\:{w}^{\mathrm{2}} −\mathrm{2} \\ $$$$\:\:\:\:\:\:\:{x}−\frac{\mathrm{1}}{{x}}\:=\:\pm\:\sqrt{{w}^{\mathrm{2}} −\mathrm{4}} \\ $$$$\:\:\:\:\:\:\:{f}\left({x}+\frac{\mathrm{1}}{{x}}\right)={x}−\frac{\mathrm{1}}{{x}} \\ $$$$\:\:\:\:\:\:{f}\left({w}\right)=\pm\sqrt{{w}^{\mathrm{2}} −\mathrm{4}} \\ $$$$\:\:\:\:{f}\left({x}\right)=\:\pm\:\sqrt{{x}^{\mathrm{2}} −\mathrm{4}}\: \\ $$$$\:\:\:\:\:\:\: \\ $$$$\:\:\:\:\:\:\:\: \\ $$
Answered by Dwaipayan Shikari last updated on 23/Dec/20
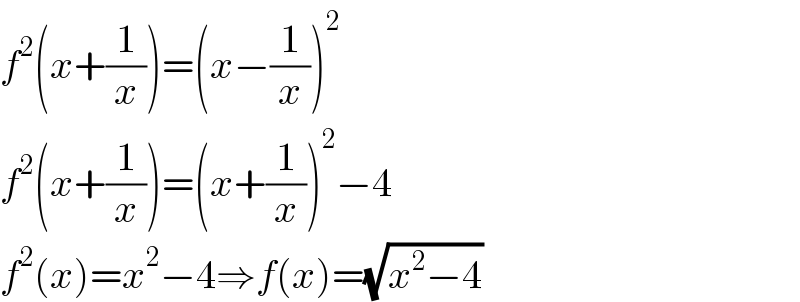
$${f}^{\mathrm{2}} \left({x}+\frac{\mathrm{1}}{{x}}\right)=\left({x}−\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} \\ $$$${f}^{\mathrm{2}} \left({x}+\frac{\mathrm{1}}{{x}}\right)=\left({x}+\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} −\mathrm{4} \\ $$$${f}^{\mathrm{2}} \left({x}\right)={x}^{\mathrm{2}} −\mathrm{4}\Rightarrow{f}\left({x}\right)=\sqrt{{x}^{\mathrm{2}} −\mathrm{4}} \\ $$
Answered by mathmax by abdo last updated on 24/Dec/20
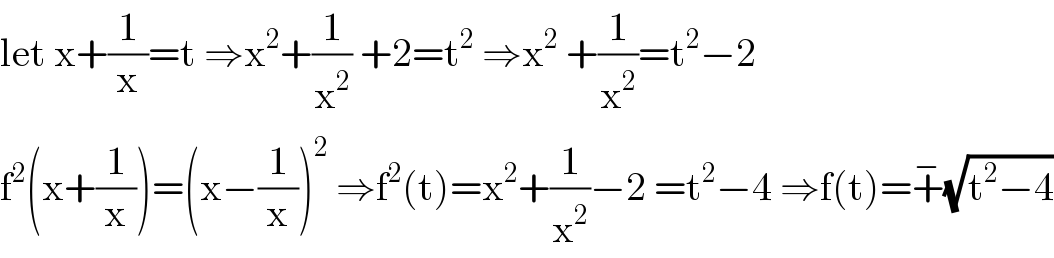
$$\mathrm{let}\:\mathrm{x}+\frac{\mathrm{1}}{\mathrm{x}}=\mathrm{t}\:\Rightarrow\mathrm{x}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }\:+\mathrm{2}=\mathrm{t}^{\mathrm{2}} \:\Rightarrow\mathrm{x}^{\mathrm{2}} \:+\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }=\mathrm{t}^{\mathrm{2}} −\mathrm{2} \\ $$$$\mathrm{f}^{\mathrm{2}} \left(\mathrm{x}+\frac{\mathrm{1}}{\mathrm{x}}\right)=\left(\mathrm{x}−\frac{\mathrm{1}}{\mathrm{x}}\right)^{\mathrm{2}} \:\Rightarrow\mathrm{f}^{\mathrm{2}} \left(\mathrm{t}\right)=\mathrm{x}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }−\mathrm{2}\:=\mathrm{t}^{\mathrm{2}} −\mathrm{4}\:\Rightarrow\mathrm{f}\left(\mathrm{t}\right)=\overset{−} {+}\sqrt{\mathrm{t}^{\mathrm{2}} −\mathrm{4}} \\ $$
