Question Number 126716 by sdfg last updated on 23/Dec/20

Answered by liberty last updated on 23/Dec/20
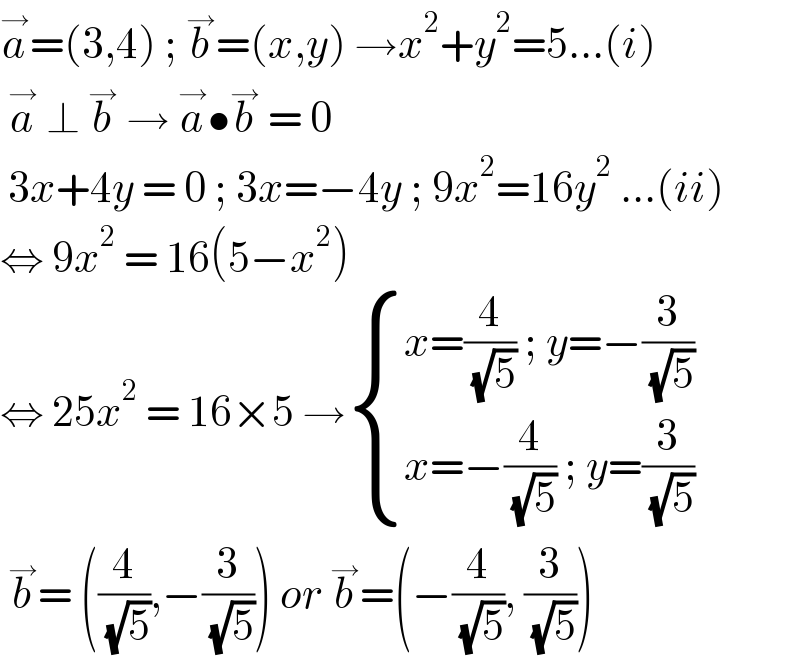
$$\overset{\rightarrow} {{a}}=\left(\mathrm{3},\mathrm{4}\right)\:;\:\overset{\rightarrow} {{b}}=\left({x},{y}\right)\:\rightarrow{x}^{\mathrm{2}} +{y}^{\mathrm{2}} =\mathrm{5}…\left({i}\right) \\ $$$$\:\overset{\rightarrow} {{a}}\:\bot\:\overset{\rightarrow} {{b}}\:\rightarrow\:\overset{\rightarrow} {{a}}\bullet\overset{\rightarrow} {{b}}\:=\:\mathrm{0} \\ $$$$\:\mathrm{3}{x}+\mathrm{4}{y}\:=\:\mathrm{0}\:;\:\mathrm{3}{x}=−\mathrm{4}{y}\:;\:\mathrm{9}{x}^{\mathrm{2}} =\mathrm{16}{y}^{\mathrm{2}} \:…\left({ii}\right) \\ $$$$\Leftrightarrow\:\mathrm{9}{x}^{\mathrm{2}} \:=\:\mathrm{16}\left(\mathrm{5}−{x}^{\mathrm{2}} \right)\: \\ $$$$\Leftrightarrow\:\mathrm{25}{x}^{\mathrm{2}} \:=\:\mathrm{16}×\mathrm{5}\:\rightarrow\begin{cases}{{x}=\frac{\mathrm{4}}{\:\sqrt{\mathrm{5}}}\:;\:{y}=−\frac{\mathrm{3}}{\:\sqrt{\mathrm{5}}}}\\{{x}=−\frac{\mathrm{4}}{\:\sqrt{\mathrm{5}}}\:;\:{y}=\frac{\mathrm{3}}{\:\sqrt{\mathrm{5}}}}\end{cases} \\ $$$$\:\overset{\rightarrow} {{b}}=\:\left(\frac{\mathrm{4}}{\:\sqrt{\mathrm{5}}},−\frac{\mathrm{3}}{\:\sqrt{\mathrm{5}}}\right)\:{or}\:\overset{\rightarrow} {{b}}=\left(−\frac{\mathrm{4}}{\:\sqrt{\mathrm{5}}},\:\frac{\mathrm{3}}{\:\sqrt{\mathrm{5}}}\right) \\ $$
