Question Number 126778 by Ar Brandon last updated on 24/Dec/20
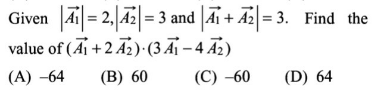
Answered by Dwaipayan Shikari last updated on 24/Dec/20
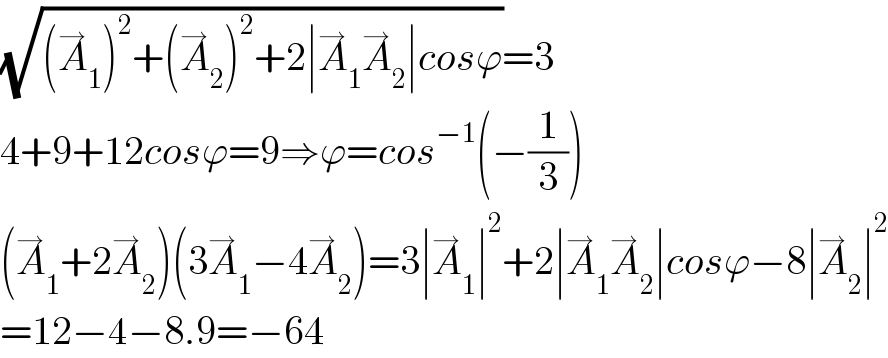
$$\sqrt{\left(\overset{\rightarrow} {{A}}_{\mathrm{1}} \right)^{\mathrm{2}} +\left(\overset{\rightarrow} {{A}}_{\mathrm{2}} \right)^{\mathrm{2}} +\mathrm{2}\mid\overset{\rightarrow} {{A}}_{\mathrm{1}} \overset{\rightarrow} {{A}}_{\mathrm{2}} \mid{cos}\varphi}=\mathrm{3} \\ $$$$\mathrm{4}+\mathrm{9}+\mathrm{12}{cos}\varphi=\mathrm{9}\Rightarrow\varphi={cos}^{−\mathrm{1}} \left(−\frac{\mathrm{1}}{\mathrm{3}}\right) \\ $$$$\left(\overset{\rightarrow} {{A}}_{\mathrm{1}} +\mathrm{2}\overset{\rightarrow} {{A}}_{\mathrm{2}} \right)\left(\mathrm{3}\overset{\rightarrow} {{A}}_{\mathrm{1}} −\mathrm{4}\overset{\rightarrow} {{A}}_{\mathrm{2}} \right)=\mathrm{3}\mid\overset{\rightarrow} {{A}}_{\mathrm{1}} \mid^{\mathrm{2}} +\mathrm{2}\mid\overset{\rightarrow} {{A}}_{\mathrm{1}} \overset{\rightarrow} {{A}}_{\mathrm{2}} \mid{cos}\varphi−\mathrm{8}\mid\overset{\rightarrow} {{A}}_{\mathrm{2}} \mid^{\mathrm{2}} \\ $$$$=\mathrm{12}−\mathrm{4}−\mathrm{8}.\mathrm{9}=−\mathrm{64} \\ $$
Answered by mr W last updated on 24/Dec/20
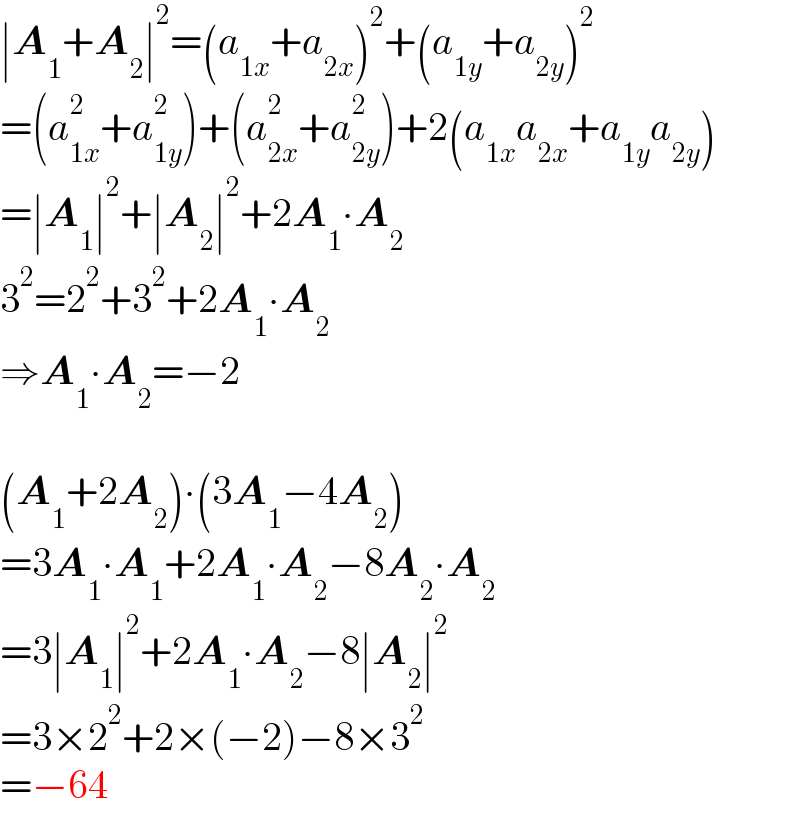
$$\mid\boldsymbol{{A}}_{\mathrm{1}} +\boldsymbol{{A}}_{\mathrm{2}} \mid^{\mathrm{2}} =\left({a}_{\mathrm{1}{x}} +{a}_{\mathrm{2}{x}} \right)^{\mathrm{2}} +\left({a}_{\mathrm{1}{y}} +{a}_{\mathrm{2}{y}} \right)^{\mathrm{2}} \\ $$$$=\left({a}_{\mathrm{1}{x}} ^{\mathrm{2}} +{a}_{\mathrm{1}{y}} ^{\mathrm{2}} \right)+\left({a}_{\mathrm{2}{x}} ^{\mathrm{2}} +{a}_{\mathrm{2}{y}} ^{\mathrm{2}} \right)+\mathrm{2}\left({a}_{\mathrm{1}{x}} {a}_{\mathrm{2}{x}} +{a}_{\mathrm{1}{y}} {a}_{\mathrm{2}{y}} \right) \\ $$$$=\mid\boldsymbol{{A}}_{\mathrm{1}} \mid^{\mathrm{2}} +\mid\boldsymbol{{A}}_{\mathrm{2}} \mid^{\mathrm{2}} +\mathrm{2}\boldsymbol{{A}}_{\mathrm{1}} \centerdot\boldsymbol{{A}}_{\mathrm{2}} \\ $$$$\mathrm{3}^{\mathrm{2}} =\mathrm{2}^{\mathrm{2}} +\mathrm{3}^{\mathrm{2}} +\mathrm{2}\boldsymbol{{A}}_{\mathrm{1}} \centerdot\boldsymbol{{A}}_{\mathrm{2}} \\ $$$$\Rightarrow\boldsymbol{{A}}_{\mathrm{1}} \centerdot\boldsymbol{{A}}_{\mathrm{2}} =−\mathrm{2} \\ $$$$ \\ $$$$\left(\boldsymbol{{A}}_{\mathrm{1}} +\mathrm{2}\boldsymbol{{A}}_{\mathrm{2}} \right)\centerdot\left(\mathrm{3}\boldsymbol{{A}}_{\mathrm{1}} −\mathrm{4}\boldsymbol{{A}}_{\mathrm{2}} \right) \\ $$$$=\mathrm{3}\boldsymbol{{A}}_{\mathrm{1}} \centerdot\boldsymbol{{A}}_{\mathrm{1}} +\mathrm{2}\boldsymbol{{A}}_{\mathrm{1}} \centerdot\boldsymbol{{A}}_{\mathrm{2}} −\mathrm{8}\boldsymbol{{A}}_{\mathrm{2}} \centerdot\boldsymbol{{A}}_{\mathrm{2}} \\ $$$$=\mathrm{3}\mid\boldsymbol{{A}}_{\mathrm{1}} \mid^{\mathrm{2}} +\mathrm{2}\boldsymbol{{A}}_{\mathrm{1}} \centerdot\boldsymbol{{A}}_{\mathrm{2}} −\mathrm{8}\mid\boldsymbol{{A}}_{\mathrm{2}} \mid^{\mathrm{2}} \\ $$$$=\mathrm{3}×\mathrm{2}^{\mathrm{2}} +\mathrm{2}×\left(−\mathrm{2}\right)−\mathrm{8}×\mathrm{3}^{\mathrm{2}} \\ $$$$=−\mathrm{64} \\ $$
