Question Number 126786 by Ar Brandon last updated on 24/Dec/20

Answered by Olaf last updated on 26/Dec/20
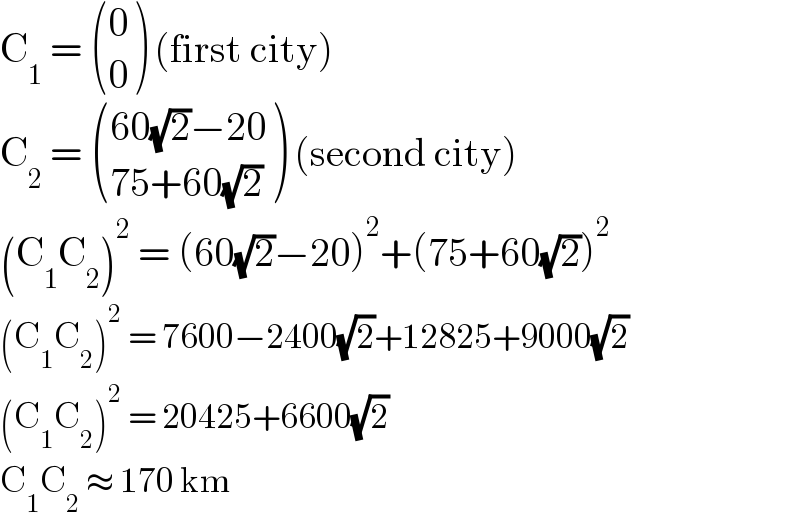
$$\mathrm{C}_{\mathrm{1}} \:=\:\begin{pmatrix}{\mathrm{0}}\\{\mathrm{0}}\end{pmatrix}\:\left(\mathrm{first}\:\mathrm{city}\right) \\ $$$$\mathrm{C}_{\mathrm{2}} \:=\:\begin{pmatrix}{\mathrm{60}\sqrt{\mathrm{2}}−\mathrm{20}}\\{\mathrm{75}+\mathrm{60}\sqrt{\mathrm{2}}}\end{pmatrix}\:\left(\mathrm{second}\:\mathrm{city}\right) \\ $$$$\left(\mathrm{C}_{\mathrm{1}} \mathrm{C}_{\mathrm{2}} \right)^{\mathrm{2}} \:=\:\left(\mathrm{60}\sqrt{\mathrm{2}}−\mathrm{20}\right)^{\mathrm{2}} +\left(\mathrm{75}+\mathrm{60}\sqrt{\mathrm{2}}\right)^{\mathrm{2}} \\ $$$$\left(\mathrm{C}_{\mathrm{1}} \mathrm{C}_{\mathrm{2}} \right)^{\mathrm{2}} \:=\:\mathrm{7600}−\mathrm{2400}\sqrt{\mathrm{2}}+\mathrm{12825}+\mathrm{9000}\sqrt{\mathrm{2}} \\ $$$$\left(\mathrm{C}_{\mathrm{1}} \mathrm{C}_{\mathrm{2}} \right)^{\mathrm{2}} \:=\:\mathrm{20425}+\mathrm{6600}\sqrt{\mathrm{2}} \\ $$$$\mathrm{C}_{\mathrm{1}} \mathrm{C}_{\mathrm{2}} \:\approx\:\mathrm{170}\:\mathrm{km} \\ $$
