Question Number 126808 by sdfg last updated on 24/Dec/20

Answered by JMZ last updated on 24/Dec/20
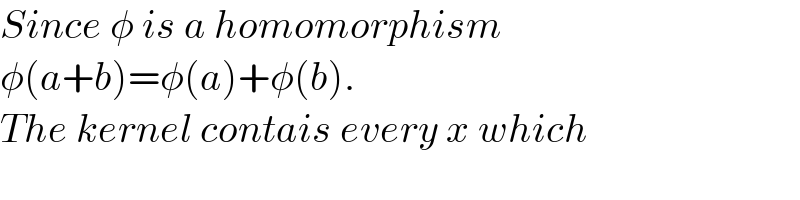
$${Since}\:\phi\:{is}\:{a}\:{homomorphism} \\ $$$$\phi\left({a}+{b}\right)=\phi\left({a}\right)+\phi\left({b}\right). \\ $$$${The}\:{kernel}\:{contais}\:{every}\:{x}\:{which} \\ $$
Answered by mindispower last updated on 24/Dec/20

$$\Leftrightarrow\varphi\left({a}−\mathrm{23}\right)=\mathrm{0} \\ $$$$\Rightarrow{a}−\mathrm{23}\in{Ker}\left(\varphi\right) \\ $$$$\Rightarrow{a}−\mathrm{23}\in\left\{\mathrm{0},\mathrm{10},\mathrm{20}\right\} \\ $$$${a}\in\left\{\mathrm{23},\mathrm{3},\mathrm{13}\right\} \\ $$
