Question Number 126835 by mohammad17 last updated on 24/Dec/20

Answered by liberty last updated on 25/Dec/20
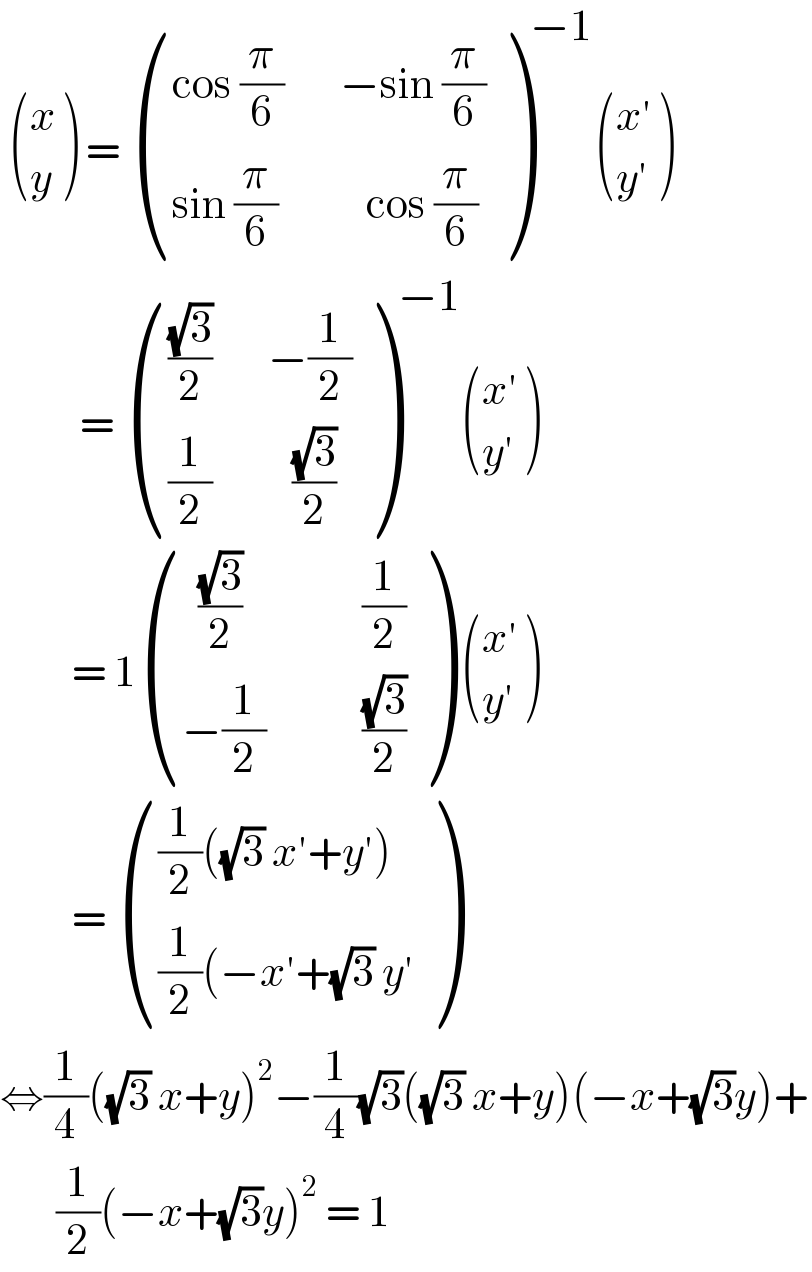
$$\:\begin{pmatrix}{{x}}\\{{y}}\end{pmatrix}\:=\:\begin{pmatrix}{\mathrm{cos}\:\frac{\pi}{\mathrm{6}}\:\:\:\:\:\:\:−\mathrm{sin}\:\frac{\pi}{\mathrm{6}}}\\{\mathrm{sin}\:\frac{\pi}{\mathrm{6}}\:\:\:\:\:\:\:\:\:\:\:\mathrm{cos}\:\frac{\pi}{\mathrm{6}}}\end{pmatrix}^{−\mathrm{1}} \begin{pmatrix}{{x}'}\\{{y}'}\end{pmatrix}\: \\ $$$$\:\:\:\:\:\:\:\:\:\:=\:\begin{pmatrix}{\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\:\:\:\:\:\:\:−\frac{\mathrm{1}}{\mathrm{2}}}\\{\frac{\mathrm{1}}{\mathrm{2}}\:\:\:\:\:\:\:\:\:\:\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}}\end{pmatrix}^{−\mathrm{1}} \begin{pmatrix}{{x}'}\\{{y}'}\end{pmatrix} \\ $$$$\:\:\:\:\:\:\:\:\:=\:\mathrm{1}\begin{pmatrix}{\:\:\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{1}}{\mathrm{2}}}\\{−\frac{\mathrm{1}}{\mathrm{2}}\:\:\:\:\:\:\:\:\:\:\:\:\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}}\end{pmatrix}\:\begin{pmatrix}{{x}'}\\{{y}'}\end{pmatrix} \\ $$$$\:\:\:\:\:\:\:\:\:=\:\begin{pmatrix}{\frac{\mathrm{1}}{\mathrm{2}}\left(\sqrt{\mathrm{3}}\:{x}'+{y}'\right)}\\{\frac{\mathrm{1}}{\mathrm{2}}\left(−{x}'+\sqrt{\mathrm{3}}\:{y}'\right.}\end{pmatrix} \\ $$$$\Leftrightarrow\frac{\mathrm{1}}{\mathrm{4}}\left(\sqrt{\mathrm{3}}\:{x}+{y}\right)^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{4}}\sqrt{\mathrm{3}}\left(\sqrt{\mathrm{3}}\:{x}+{y}\right)\left(−{x}+\sqrt{\mathrm{3}}{y}\right)+ \\ $$$$\:\:\:\:\:\:\:\frac{\mathrm{1}}{\mathrm{2}}\left(−{x}+\sqrt{\mathrm{3}}{y}\right)^{\mathrm{2}} \:=\:\mathrm{1} \\ $$
