Menu Close

Question-126854

Tinku Tara 0 Comments
Pin




Question Number 126854 by sdfg last updated on 24/Dec/20
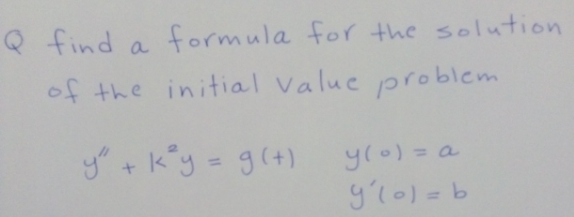
Answered by mathmax by abdo last updated on 24/Dec/20
h→r^2 +k^2 =0 ⇒r^2 =−k^2 ⇒r =+^− ik ⇒y_h =ae^(ikx) +be^(−ikx) =αcos(kx)+βsin(kx) =αu_1 +βu_2 w(u_1 ,u_2 )= determinant (((cos(kx) sin(kx))),((−ksin(kx) kcos(x))))=k (we suppose k≠o) w_1 = determinant (((o sin(kx))),((g(x) kcos(kx))))=−sin(kx)g(x) w_2 = determinant (((cos(kx) 0)),((−ksin(kx) g(x))))=cos(kx)g(x) v_1 =∫ (w_1 /w)dx =−(1/k)∫ sin(kx)g(x)dx v_2 =∫ (w_2 /w)dx =(1/k)∫ cos(kx)g(x)dx ⇒ y_p =u_1 v_1 +u_2 v_2 =−(1/k)cos(kx)∫_0 ^x sin(kt)g(t)dt+(1/k)sin(kx) ∫_0 ^x cos(kt)g(t)dt ⇒y(x)=y_h +y_p =αcos(kx)+βsin(kx)−(1/k)cos(kx)∫_0 ^x sin(kt)g(t)dt+(1/k)sin(kx)∫_0 ^x cos(kt)g(t)dt y(0)=a ⇒α=a y^′ (x)=−αksin(kx)+βkcos(kx)−(1/k){ksin(kx)∫_0 ^x sin(kt)g(t)dt +cos(kx)sin(kx)g(x)}+(1/k){kcos(kx)∫_0 ^x cos(kt)g(t)dt +sin(kx)cos(kx)g(x)} =−αk sin(kx)+βk cos(kx)−sin(kx)∫_0 ^x sin(kt)g(t)dt +cos(kx)∫_0 ^x cos(kt)g(t)dt y^′ (0)=b ⇒βk =b ⇒β =(b/k) so y(x)is known
$$\mathrm{h}\rightarrow\mathrm{r}^{\mathrm{2}} \:+\mathrm{k}^{\mathrm{2}} =\mathrm{0}\:\Rightarrow\mathrm{r}^{\mathrm{2}} =−\mathrm{k}^{\mathrm{2}} \:\Rightarrow\mathrm{r}\:=\overset{−} {+}\mathrm{ik}\:\Rightarrow\mathrm{y}_{\mathrm{h}} =\mathrm{ae}^{\mathrm{ikx}} \:+\mathrm{be}^{−\mathrm{ikx}} \\ $$$$=\alpha\mathrm{cos}\left(\mathrm{kx}\right)+\beta\mathrm{sin}\left(\mathrm{kx}\right)\:=\alpha\mathrm{u}_{\mathrm{1}} \:+\beta\mathrm{u}_{\mathrm{2}} \\ $$$$\mathrm{w}\left(\mathrm{u}_{\mathrm{1}} ,\mathrm{u}_{\mathrm{2}} \right)=\begin{vmatrix}{\mathrm{cos}\left(\mathrm{kx}\right)\:\:\:\:\:\:\:\:\mathrm{sin}\left(\mathrm{kx}\right)}\\{−\mathrm{ksin}\left(\mathrm{kx}\right)\:\:\:\:\:\:\:\mathrm{kcos}\left(\mathrm{x}\right)}\end{vmatrix}=\mathrm{k}\:\:\:\:\:\left(\mathrm{we}\:\mathrm{suppose}\:\mathrm{k}\neq\mathrm{o}\right) \\ $$$$\mathrm{w}_{\mathrm{1}} =\begin{vmatrix}{\mathrm{o}\:\:\:\:\:\:\:\mathrm{sin}\left(\mathrm{kx}\right)}\\{\mathrm{g}\left(\mathrm{x}\right)\:\:\:\:\:\:\mathrm{kcos}\left(\mathrm{kx}\right)}\end{vmatrix}=−\mathrm{sin}\left(\mathrm{kx}\right)\mathrm{g}\left(\mathrm{x}\right) \\ $$$$\mathrm{w}_{\mathrm{2}} =\begin{vmatrix}{\mathrm{cos}\left(\mathrm{kx}\right)\:\:\:\:\:\:\:\:\:\mathrm{0}}\\{−\mathrm{ksin}\left(\mathrm{kx}\right)\:\:\:\:\mathrm{g}\left(\mathrm{x}\right)}\end{vmatrix}=\mathrm{cos}\left(\mathrm{kx}\right)\mathrm{g}\left(\mathrm{x}\right) \\ $$$$\mathrm{v}_{\mathrm{1}} =\int\:\frac{\mathrm{w}_{\mathrm{1}} }{\mathrm{w}}\mathrm{dx}\:=−\frac{\mathrm{1}}{\mathrm{k}}\int\:\mathrm{sin}\left(\mathrm{kx}\right)\mathrm{g}\left(\mathrm{x}\right)\mathrm{dx} \\ $$$$\mathrm{v}_{\mathrm{2}} =\int\:\frac{\mathrm{w}_{\mathrm{2}} }{\mathrm{w}}\mathrm{dx}\:=\frac{\mathrm{1}}{\mathrm{k}}\int\:\mathrm{cos}\left(\mathrm{kx}\right)\mathrm{g}\left(\mathrm{x}\right)\mathrm{dx}\:\Rightarrow \\ $$$$\mathrm{y}_{\mathrm{p}} =\mathrm{u}_{\mathrm{1}} \mathrm{v}_{\mathrm{1}} +\mathrm{u}_{\mathrm{2}} \mathrm{v}_{\mathrm{2}} \:\:=−\frac{\mathrm{1}}{\mathrm{k}}\mathrm{cos}\left(\mathrm{kx}\right)\int_{\mathrm{0}} ^{\mathrm{x}} \:\:\mathrm{sin}\left(\mathrm{kt}\right)\mathrm{g}\left(\mathrm{t}\right)\mathrm{dt}+\frac{\mathrm{1}}{\mathrm{k}}\mathrm{sin}\left(\mathrm{kx}\right)\:\int_{\mathrm{0}} ^{\mathrm{x}} \mathrm{cos}\left(\mathrm{kt}\right)\mathrm{g}\left(\mathrm{t}\right)\mathrm{dt} \\ $$$$\Rightarrow\mathrm{y}\left(\mathrm{x}\right)=\mathrm{y}_{\mathrm{h}} +\mathrm{y}_{\mathrm{p}} \\ $$$$=\alpha\mathrm{cos}\left(\mathrm{kx}\right)+\beta\mathrm{sin}\left(\mathrm{kx}\right)−\frac{\mathrm{1}}{\mathrm{k}}\mathrm{cos}\left(\mathrm{kx}\right)\int_{\mathrm{0}} ^{\mathrm{x}} \mathrm{sin}\left(\mathrm{kt}\right)\mathrm{g}\left(\mathrm{t}\right)\mathrm{dt}+\frac{\mathrm{1}}{\mathrm{k}}\mathrm{sin}\left(\mathrm{kx}\right)\int_{\mathrm{0}} ^{\mathrm{x}} \mathrm{cos}\left(\mathrm{kt}\right)\mathrm{g}\left(\mathrm{t}\right)\mathrm{dt} \\ $$$$\mathrm{y}\left(\mathrm{0}\right)=\mathrm{a}\:\Rightarrow\alpha=\mathrm{a} \\ $$$$\mathrm{y}^{'} \left(\mathrm{x}\right)=−\alpha\mathrm{ksin}\left(\mathrm{kx}\right)+\beta\mathrm{kcos}\left(\mathrm{kx}\right)−\frac{\mathrm{1}}{\mathrm{k}}\left\{\mathrm{ksin}\left(\mathrm{kx}\right)\int_{\mathrm{0}} ^{\mathrm{x}} \mathrm{sin}\left(\mathrm{kt}\right)\mathrm{g}\left(\mathrm{t}\right)\mathrm{dt}\right. \\ $$$$\left.+\mathrm{cos}\left(\mathrm{kx}\right)\mathrm{sin}\left(\mathrm{kx}\right)\mathrm{g}\left(\mathrm{x}\right)\right\}+\frac{\mathrm{1}}{\mathrm{k}}\left\{\mathrm{kcos}\left(\mathrm{kx}\right)\int_{\mathrm{0}} ^{\mathrm{x}} \mathrm{cos}\left(\mathrm{kt}\right)\mathrm{g}\left(\mathrm{t}\right)\mathrm{dt}\right. \\ $$$$\left.+\mathrm{sin}\left(\mathrm{kx}\right)\mathrm{cos}\left(\mathrm{kx}\right)\mathrm{g}\left(\mathrm{x}\right)\right\} \\ $$$$=−\alpha\mathrm{k}\:\mathrm{sin}\left(\mathrm{kx}\right)+\beta\mathrm{k}\:\mathrm{cos}\left(\mathrm{kx}\right)−\mathrm{sin}\left(\mathrm{kx}\right)\int_{\mathrm{0}} ^{\mathrm{x}} \:\mathrm{sin}\left(\mathrm{kt}\right)\mathrm{g}\left(\mathrm{t}\right)\mathrm{dt} \\ $$$$+\mathrm{cos}\left(\mathrm{kx}\right)\int_{\mathrm{0}} ^{\mathrm{x}} \:\mathrm{cos}\left(\mathrm{kt}\right)\mathrm{g}\left(\mathrm{t}\right)\mathrm{dt} \\ $$$$\mathrm{y}^{'} \left(\mathrm{0}\right)=\mathrm{b}\:\Rightarrow\beta\mathrm{k}\:\:=\mathrm{b}\:\Rightarrow\beta\:=\frac{\mathrm{b}}{\mathrm{k}}\:\:\mathrm{so}\:\mathrm{y}\left(\mathrm{x}\right)\mathrm{is}\:\mathrm{known} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *