Question Number 126859 by sdfg last updated on 24/Dec/20

Answered by mr W last updated on 24/Dec/20
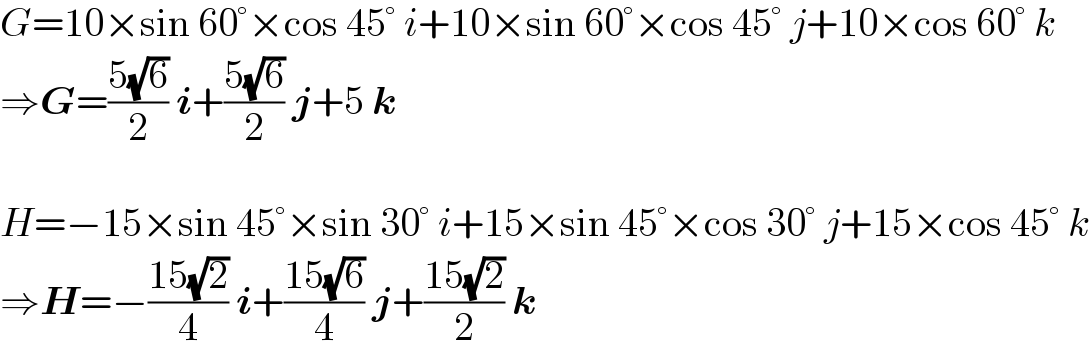
$${G}=\mathrm{10}×\mathrm{sin}\:\mathrm{60}°×\mathrm{cos}\:\mathrm{45}°\:{i}+\mathrm{10}×\mathrm{sin}\:\mathrm{60}°×\mathrm{cos}\:\mathrm{45}°\:{j}+\mathrm{10}×\mathrm{cos}\:\mathrm{60}°\:{k} \\ $$$$\Rightarrow\boldsymbol{{G}}=\frac{\mathrm{5}\sqrt{\mathrm{6}}}{\mathrm{2}}\:\boldsymbol{{i}}+\frac{\mathrm{5}\sqrt{\mathrm{6}}}{\mathrm{2}}\:\boldsymbol{{j}}+\mathrm{5}\:\boldsymbol{{k}} \\ $$$$ \\ $$$${H}=−\mathrm{15}×\mathrm{sin}\:\mathrm{45}°×\mathrm{sin}\:\mathrm{30}°\:{i}+\mathrm{15}×\mathrm{sin}\:\mathrm{45}°×\mathrm{cos}\:\mathrm{30}°\:{j}+\mathrm{15}×\mathrm{cos}\:\mathrm{45}°\:{k} \\ $$$$\Rightarrow\boldsymbol{{H}}=−\frac{\mathrm{15}\sqrt{\mathrm{2}}}{\mathrm{4}}\:\boldsymbol{{i}}+\frac{\mathrm{15}\sqrt{\mathrm{6}}}{\mathrm{4}}\:\boldsymbol{{j}}+\frac{\mathrm{15}\sqrt{\mathrm{2}}}{\mathrm{2}}\:\boldsymbol{{k}} \\ $$
