Question Number 127032 by mnjuly1970 last updated on 26/Dec/20
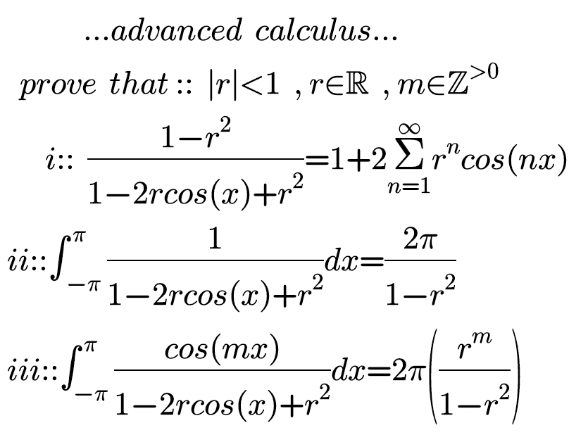
Answered by Olaf last updated on 26/Dec/20
![i) 1−2rcosx+r^2 = (e^(ix) −r)(e^(−ix) −r) R_x (r) = ((1−r^2 )/(1−2rcosx+r^2 )) = ((1−r^2 )/((e^(ix) −r)(e^(−ix) −r))) = −1+((A(x))/(e^(ix) −r))+((B(x))/(e^(−ix) −r)) A(x) = ((1−e^(2ix) )/(e^(−ix) −e^(ix) )) = e^(ix) B(x) = ((1−e^(−2ix) )/(e^(ix) −e^(−ix) )) = e^(−ix) R_x (r) = −1+(e^(ix) /(e^(ix) −r))+(e^(−ix) /(e^(−ix) −r)) R_x (r) = −1+(1/(1−e^(−ix) r))+(1/(1−e^(ix) r)) R_x (r) = −1+Σ_(n=0) ^∞ e^(−inx) r^n +Σ_(n=0) ^∞ e^(inx) r^n R_x (r) = −1+2Σ_(n=0) ^∞ ((e^(inx) +e^(−inx) )/2)r^n R_x (r) = 1+2Σ_(n=1) ^∞ cos(nx)r^n ii) F(r) = (1/(1−r^2 ))∫_(−π) ^(+π) R_x (r)dx F(r) = (2/(1−r^2 ))[x+2Σ_(n=1) ^∞ ((sin(nx))/n)r^n ]_0 ^π F(r) = ((2π)/(1−r^2 )) iii) G(r) = ∫_(−π) ^(+π) ((cos(mx))/(1−2rcosx+r^2 ))dx G(r) = (1/(1−r^2 ))∫_(−π) ^(+π) [cos(mx)+2Σ_(n=1) ^∞ cos(mx)cos(nx)r^n dx G(r) = (2/(1−r^2 ))∫_0 ^(+π) [Σ_(n=1) ^∞ [cos((m+n)x)+cos((m−n)x)]r^n dx different of 0 only for m = n G(r) = (2/(1−r^2 ))[r^m x]_0 ^π = ((2πr^m )/(1−r^2 ))](https://www.tinkutara.com/question/Q127039.png)
$$\left.{i}\right) \\ $$$$\mathrm{1}−\mathrm{2}{r}\mathrm{cos}{x}+{r}^{\mathrm{2}} \:=\:\left({e}^{{ix}} −{r}\right)\left({e}^{−{ix}} −{r}\right) \\ $$$$\mathrm{R}_{{x}} \left({r}\right)\:=\:\frac{\mathrm{1}−{r}^{\mathrm{2}} }{\mathrm{1}−\mathrm{2}{r}\mathrm{cos}{x}+{r}^{\mathrm{2}} }\:=\:\frac{\mathrm{1}−{r}^{\mathrm{2}} }{\left({e}^{{ix}} −{r}\right)\left({e}^{−{ix}} −{r}\right)} \\ $$$$=\:−\mathrm{1}+\frac{\mathrm{A}\left({x}\right)}{{e}^{{ix}} −{r}}+\frac{\mathrm{B}\left({x}\right)}{{e}^{−{ix}} −{r}} \\ $$$$\mathrm{A}\left({x}\right)\:=\:\frac{\mathrm{1}−{e}^{\mathrm{2}{ix}} }{{e}^{−{ix}} −{e}^{{ix}} }\:=\:{e}^{{ix}} \\ $$$$\mathrm{B}\left({x}\right)\:=\:\frac{\mathrm{1}−{e}^{−\mathrm{2}{ix}} }{{e}^{{ix}} −{e}^{−{ix}} }\:=\:{e}^{−{ix}} \\ $$$$\mathrm{R}_{{x}} \left({r}\right)\:=\:−\mathrm{1}+\frac{{e}^{{ix}} }{{e}^{{ix}} −{r}}+\frac{{e}^{−{ix}} }{{e}^{−{ix}} −{r}} \\ $$$$\mathrm{R}_{{x}} \left({r}\right)\:=\:−\mathrm{1}+\frac{\mathrm{1}}{\mathrm{1}−{e}^{−{ix}} {r}}+\frac{\mathrm{1}}{\mathrm{1}−{e}^{{ix}} {r}} \\ $$$$\mathrm{R}_{{x}} \left({r}\right)\:=\:−\mathrm{1}+\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}{e}^{−{inx}} {r}^{{n}} +\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}{e}^{{inx}} {r}^{{n}} \\ $$$$\mathrm{R}_{{x}} \left({r}\right)\:=\:−\mathrm{1}+\mathrm{2}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{{e}^{{inx}} +{e}^{−{inx}} }{\mathrm{2}}{r}^{{n}} \\ $$$$\mathrm{R}_{{x}} \left({r}\right)\:=\:\mathrm{1}+\mathrm{2}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\mathrm{cos}\left({nx}\right){r}^{{n}} \\ $$$$\left.{ii}\right) \\ $$$$\mathrm{F}\left({r}\right)\:=\:\frac{\mathrm{1}}{\mathrm{1}−{r}^{\mathrm{2}} }\int_{−\pi} ^{+\pi} \mathrm{R}_{{x}} \left({r}\right){dx} \\ $$$$\mathrm{F}\left({r}\right)\:=\:\frac{\mathrm{2}}{\mathrm{1}−{r}^{\mathrm{2}} }\left[{x}+\mathrm{2}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{sin}\left({nx}\right)}{{n}}{r}^{{n}} \right]_{\mathrm{0}} ^{\pi} \\ $$$$\mathrm{F}\left({r}\right)\:=\:\frac{\mathrm{2}\pi}{\mathrm{1}−{r}^{\mathrm{2}} } \\ $$$$\left.{iii}\right) \\ $$$$\mathrm{G}\left({r}\right)\:=\:\int_{−\pi} ^{+\pi} \frac{\mathrm{cos}\left({mx}\right)}{\mathrm{1}−\mathrm{2}{r}\mathrm{cos}{x}+{r}^{\mathrm{2}} }{dx} \\ $$$$\mathrm{G}\left({r}\right)\:=\:\frac{\mathrm{1}}{\mathrm{1}−{r}^{\mathrm{2}} }\int_{−\pi} ^{+\pi} \left[\mathrm{cos}\left({mx}\right)+\mathrm{2}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\mathrm{cos}\left({mx}\right)\mathrm{cos}\left({nx}\right){r}^{{n}} {dx}\right. \\ $$$$\mathrm{G}\left({r}\right)\:=\:\frac{\mathrm{2}}{\mathrm{1}−{r}^{\mathrm{2}} }\int_{\mathrm{0}} ^{+\pi} \left[\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left[\mathrm{cos}\left(\left({m}+{n}\right){x}\right)+\mathrm{cos}\left(\left({m}−{n}\right){x}\right)\right]{r}^{{n}} {dx}\right. \\ $$$$\mathrm{different}\:\mathrm{of}\:\mathrm{0}\:\mathrm{only}\:\mathrm{for}\:{m}\:=\:{n} \\ $$$$\mathrm{G}\left({r}\right)\:=\:\frac{\mathrm{2}}{\mathrm{1}−{r}^{\mathrm{2}} }\left[{r}^{{m}} {x}\right]_{\mathrm{0}} ^{\pi} \:=\:\frac{\mathrm{2}\pi{r}^{{m}} }{\mathrm{1}−{r}^{\mathrm{2}} } \\ $$
Commented by mnjuly1970 last updated on 26/Dec/20
$${very}\:{nice}\:{solution}\:{mr}\:{olaf} \\ $$$${grateful}.. \\ $$
Answered by Dwaipayan Shikari last updated on 26/Dec/20
![∫_(−π) ^π (dx/(1−2rcosx+r^2 ))=2∫_(−∞) ^∞ (dt/(1−((2r(1−t^2 ))/(1+t^2 ))+r^2 )) .(1/(t^2 +1)) t=tan(x/2) =2∫_(−∞) ^∞ (dt/(1+t^2 −2r+2rt^2 +r^2 +r^2 t^2 ))=∫_(−∞) ^∞ (dt/(t^2 (r^2 +2r+1)+r^2 −2r+1)) =[(2/(1−r^2 ))tan^(−1) (t/((r−1)/(r+1)))]_(−∞) ^∞ =((2π)/(1−r^2 ))](https://www.tinkutara.com/question/Q127041.png)
$$\int_{−\pi} ^{\pi} \frac{{dx}}{\mathrm{1}−\mathrm{2}{rcosx}+{r}^{\mathrm{2}} }=\mathrm{2}\int_{−\infty} ^{\infty} \frac{{dt}}{\mathrm{1}−\frac{\mathrm{2}{r}\left(\mathrm{1}−{t}^{\mathrm{2}} \right)}{\mathrm{1}+{t}^{\mathrm{2}} }+{r}^{\mathrm{2}} }\:.\frac{\mathrm{1}}{{t}^{\mathrm{2}} +\mathrm{1}}\:\:\:\:\:{t}={tan}\frac{{x}}{\mathrm{2}} \\ $$$$=\mathrm{2}\int_{−\infty} ^{\infty} \frac{{dt}}{\mathrm{1}+{t}^{\mathrm{2}} −\mathrm{2}{r}+\mathrm{2}{rt}^{\mathrm{2}} +{r}^{\mathrm{2}} +{r}^{\mathrm{2}} {t}^{\mathrm{2}} }=\int_{−\infty} ^{\infty} \frac{{dt}}{{t}^{\mathrm{2}} \left({r}^{\mathrm{2}} +\mathrm{2}{r}+\mathrm{1}\right)+{r}^{\mathrm{2}} −\mathrm{2}{r}+\mathrm{1}} \\ $$$$=\left[\frac{\mathrm{2}}{\mathrm{1}−{r}^{\mathrm{2}} }{tan}^{−\mathrm{1}} \frac{{t}}{\frac{{r}−\mathrm{1}}{{r}+\mathrm{1}}}\right]_{−\infty} ^{\infty} =\frac{\mathrm{2}\pi}{\mathrm{1}−{r}^{\mathrm{2}} } \\ $$
Commented by mnjuly1970 last updated on 26/Dec/20

$${thanks}\:{alot}\:{mr}\:{payan}… \\ $$
