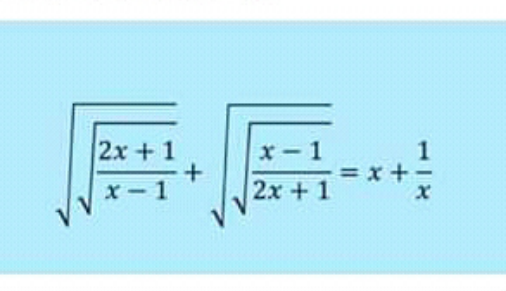
Question Number 127158 by Jamshidbek last updated on 27/Dec/20
Commented by mr W last updated on 27/Dec/20

$${x}=\phi={golden}\:{ratio}\approx\mathrm{1}.\mathrm{618} \\ $$
Answered by mindispower last updated on 28/Dec/20
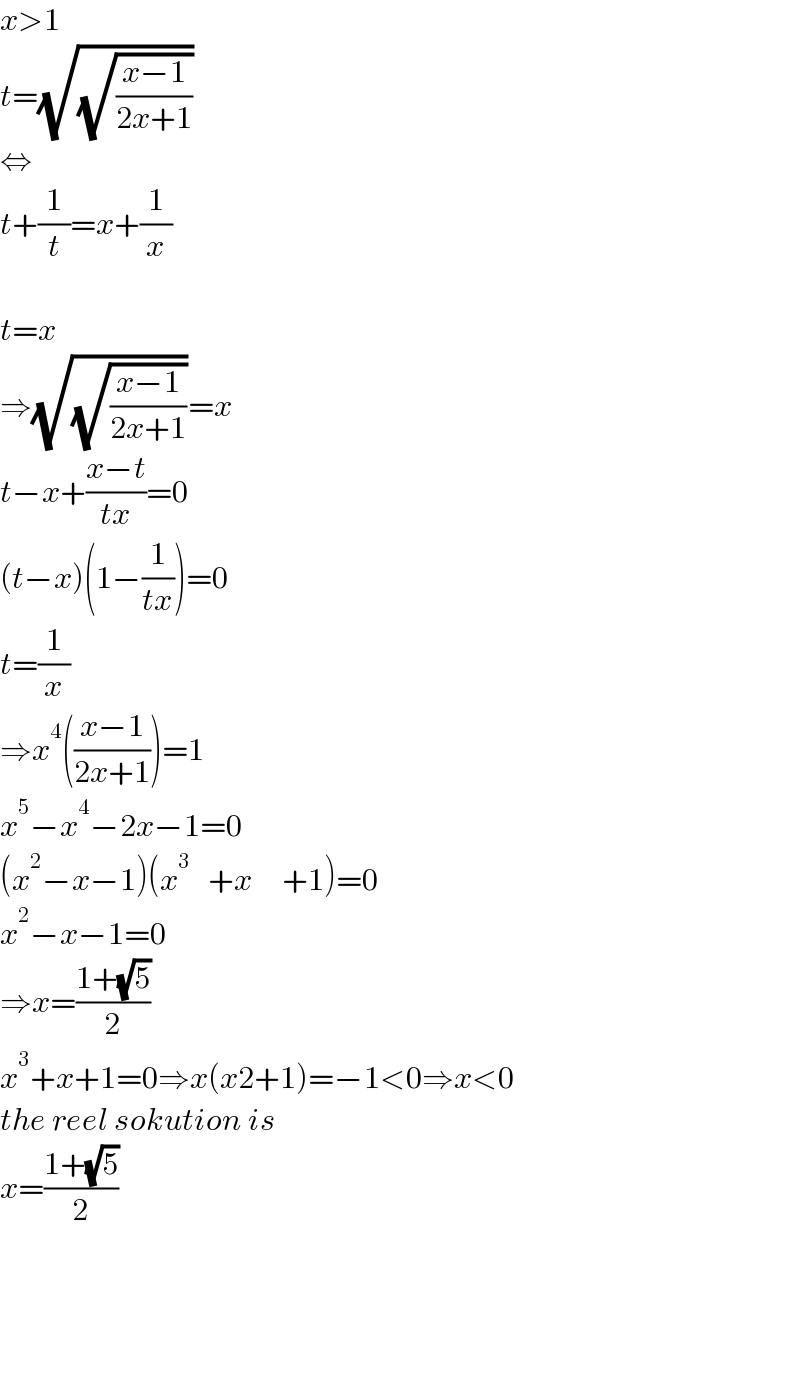
$${x}>\mathrm{1} \\ $$$${t}=\sqrt{\sqrt{\frac{{x}−\mathrm{1}}{\mathrm{2}{x}+\mathrm{1}}}} \\ $$$$\Leftrightarrow \\ $$$${t}+\frac{\mathrm{1}}{{t}}={x}+\frac{\mathrm{1}}{{x}} \\ $$$$ \\ $$$${t}={x} \\ $$$$\Rightarrow\sqrt{\sqrt{\frac{{x}−\mathrm{1}}{\mathrm{2}{x}+\mathrm{1}}}}={x} \\ $$$${t}−{x}+\frac{{x}−{t}}{{tx}}=\mathrm{0} \\ $$$$\left({t}−{x}\right)\left(\mathrm{1}−\frac{\mathrm{1}}{{tx}}\right)=\mathrm{0} \\ $$$${t}=\frac{\mathrm{1}}{{x}} \\ $$$$\Rightarrow{x}^{\mathrm{4}} \left(\frac{{x}−\mathrm{1}}{\mathrm{2}{x}+\mathrm{1}}\right)=\mathrm{1} \\ $$$${x}^{\mathrm{5}} −{x}^{\mathrm{4}} −\mathrm{2}{x}−\mathrm{1}=\mathrm{0} \\ $$$$\left({x}^{\mathrm{2}} −{x}−\mathrm{1}\right)\left({x}^{\mathrm{3}} \:\:\:+{x}\:\:\:\:\:+\mathrm{1}\right)=\mathrm{0} \\ $$$${x}^{\mathrm{2}} −{x}−\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow{x}=\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$$${x}^{\mathrm{3}} +{x}+\mathrm{1}=\mathrm{0}\Rightarrow{x}\left({x}\mathrm{2}+\mathrm{1}\right)=−\mathrm{1}<\mathrm{0}\Rightarrow{x}<\mathrm{0} \\ $$$${the}\:{reel}\:{sokution}\:{is} \\ $$$${x}=\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
