Question Number 127247 by ZiYangLee last updated on 28/Dec/20

Answered by mr W last updated on 28/Dec/20
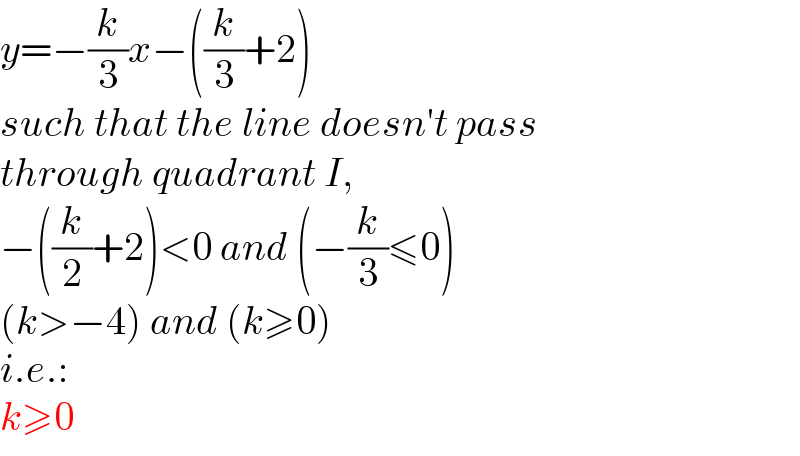
$${y}=−\frac{{k}}{\mathrm{3}}{x}−\left(\frac{{k}}{\mathrm{3}}+\mathrm{2}\right) \\ $$$${such}\:{that}\:{the}\:{line}\:{doesn}'{t}\:{pass} \\ $$$${through}\:{quadrant}\:{I}, \\ $$$$−\left(\frac{{k}}{\mathrm{2}}+\mathrm{2}\right)<\mathrm{0}\:{and}\:\left(−\frac{{k}}{\mathrm{3}}\leqslant\mathrm{0}\right) \\ $$$$\left({k}>−\mathrm{4}\right)\:{and}\:\left({k}\geqslant\mathrm{0}\right) \\ $$$${i}.{e}.: \\ $$$${k}\geqslant\mathrm{0} \\ $$
Commented by mr W last updated on 28/Dec/20
Commented by mr W last updated on 28/Dec/20
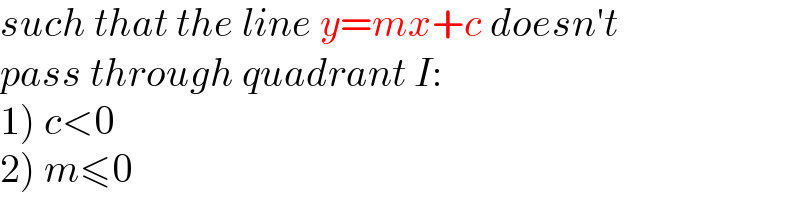
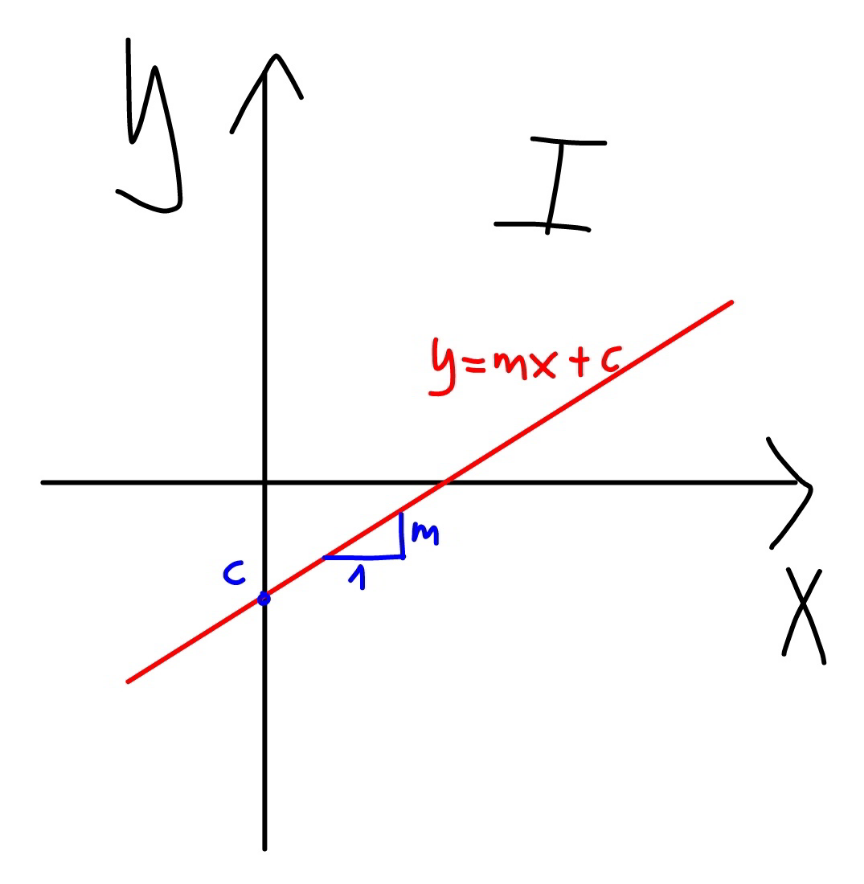
$${such}\:{that}\:{the}\:{line}\:{y}={mx}+{c}\:{doesn}'{t} \\ $$$${pass}\:{through}\:{quadrant}\:{I}: \\ $$$$\left.\mathrm{1}\right)\:{c}<\mathrm{0} \\ $$$$\left.\mathrm{2}\right)\:{m}\leqslant\mathrm{0} \\ $$
