Question Number 127307 by Study last updated on 28/Dec/20
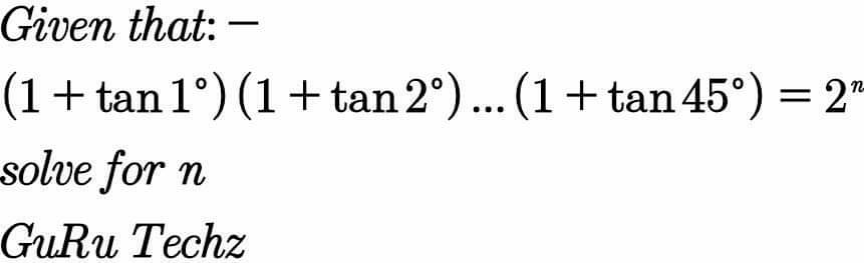
Commented by Dwaipayan Shikari last updated on 28/Dec/20

$${n}=\mathrm{23} \\ $$
Commented by Study last updated on 28/Dec/20
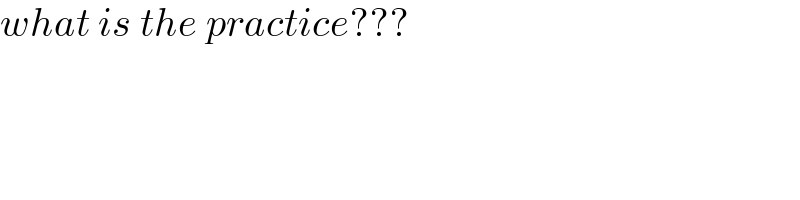
$${what}\:{is}\:{the}\:{practice}??? \\ $$
Answered by Olaf last updated on 28/Dec/20

$$\mathrm{P}\:=\:\underset{{k}=\mathrm{1}} {\overset{\mathrm{45}} {\prod}}\left(\mathrm{1}+\mathrm{tan}{k}°\right) \\ $$$$\mathrm{P}\:=\:\frac{\underset{{k}=\mathrm{1}} {\overset{\mathrm{45}} {\prod}}\left(\mathrm{cos}{k}°+\mathrm{sin}{k}°\right)}{\underset{{k}=\mathrm{1}} {\overset{\mathrm{45}} {\prod}}\mathrm{cos}{k}°} \\ $$$$\mathrm{P}\:=\:\frac{\underset{{k}=\mathrm{1}} {\overset{\mathrm{45}} {\prod}}\sqrt{\mathrm{2}}\mathrm{cos}\left(\mathrm{45}°−{k}°\right)}{\underset{{k}=\mathrm{1}} {\overset{\mathrm{45}} {\prod}}\mathrm{cos}{k}°} \\ $$$$\mathrm{P}\:=\:\mathrm{2}^{\mathrm{22}} \sqrt{\mathrm{2}}\frac{\underset{{k}=\mathrm{0}} {\overset{\mathrm{44}} {\prod}}\mathrm{cos}{k}°}{\underset{{k}=\mathrm{1}} {\overset{\mathrm{45}} {\prod}}\mathrm{cos}{k}°} \\ $$$$\mathrm{P}\:=\:\mathrm{2}^{\mathrm{22}} \sqrt{\mathrm{2}}\frac{\mathrm{cos0}°}{\mathrm{cos45}°} \\ $$$$\mathrm{P}\:=\:\mathrm{2}^{\mathrm{22}} \sqrt{\mathrm{2}}×\frac{\mathrm{1}}{\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}}\:=\:\mathrm{2}^{\mathrm{23}} \\ $$$$\Rightarrow\:{n}\:=\:\mathrm{23} \\ $$
Answered by Dwaipayan Shikari last updated on 28/Dec/20
![1+tan1°=1+((1−tan44°)/(1+tan44°))=(2/(1+tan44°)) 1+tan2°=(2/(1+tan43°)) (1+tan1°)(1+tan2°)....(1+tan45°) =[(1+tan1°)(1+tan44°)][(1+tan2°)(1+tan43°)]....(1+1) =2.2.2.2..2=2^(23)](https://www.tinkutara.com/question/Q127314.png)
$$\mathrm{1}+{tan}\mathrm{1}°=\mathrm{1}+\frac{\mathrm{1}−{tan}\mathrm{44}°}{\mathrm{1}+{tan}\mathrm{44}°}=\frac{\mathrm{2}}{\mathrm{1}+{tan}\mathrm{44}°} \\ $$$$\mathrm{1}+{tan}\mathrm{2}°=\frac{\mathrm{2}}{\mathrm{1}+{tan}\mathrm{43}°} \\ $$$$\left(\mathrm{1}+{tan}\mathrm{1}°\right)\left(\mathrm{1}+{tan}\mathrm{2}°\right)….\left(\mathrm{1}+{tan}\mathrm{45}°\right) \\ $$$$=\left[\left(\mathrm{1}+{tan}\mathrm{1}°\right)\left(\mathrm{1}+{tan}\mathrm{44}°\right)\right]\left[\left(\mathrm{1}+{tan}\mathrm{2}°\right)\left(\mathrm{1}+{tan}\mathrm{43}°\right)\right]….\left(\mathrm{1}+\mathrm{1}\right) \\ $$$$=\mathrm{2}.\mathrm{2}.\mathrm{2}.\mathrm{2}..\mathrm{2}=\mathrm{2}^{\mathrm{23}} \\ $$
Commented by Study last updated on 28/Dec/20

$${thanks}\:{sir} \\ $$
