Question Number 127460 by ajfour last updated on 30/Dec/20

Commented by ajfour last updated on 30/Dec/20
$${Q}.\mathrm{127127}\:\:\:\left({Revisit}\right) \\ $$$${Given}\:\:{p},{q}\:\:\:;\:\:{find}\:{R}. \\ $$
Answered by ajfour last updated on 30/Dec/20
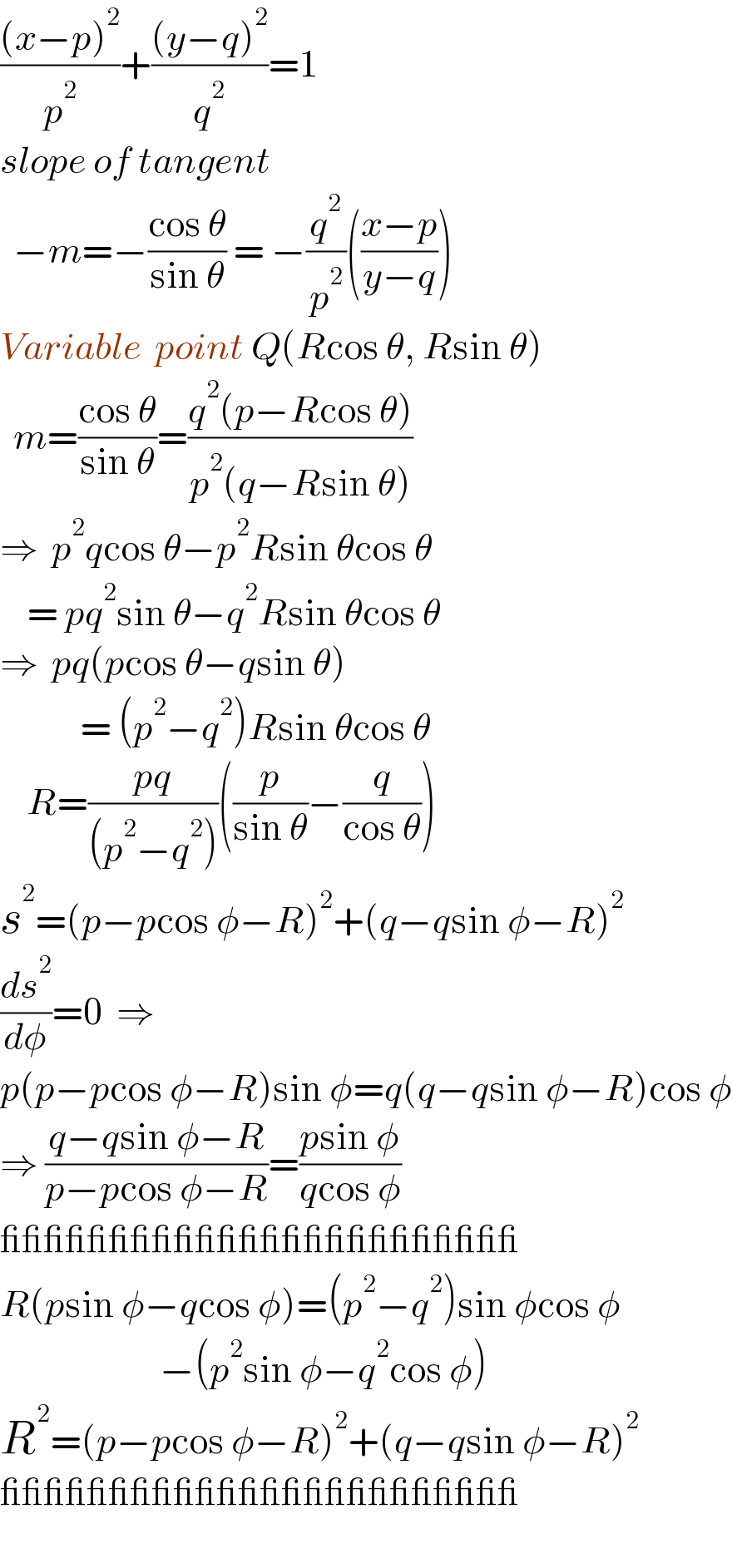
$$\frac{\left({x}−{p}\right)^{\mathrm{2}} }{{p}^{\mathrm{2}} }+\frac{\left({y}−{q}\right)^{\mathrm{2}} }{{q}^{\mathrm{2}} }=\mathrm{1} \\ $$$${slope}\:{of}\:{tangent} \\ $$$$\:\:−{m}=−\frac{\mathrm{cos}\:\theta}{\mathrm{sin}\:\theta}\:=\:−\frac{{q}^{\mathrm{2}} }{{p}^{\mathrm{2}} }\left(\frac{{x}−{p}}{{y}−{q}}\right) \\ $$$${Variable}\:\:{point}\:{Q}\left({R}\mathrm{cos}\:\theta,\:{R}\mathrm{sin}\:\theta\right) \\ $$$$\:\:{m}=\frac{\mathrm{cos}\:\theta}{\mathrm{sin}\:\theta}=\frac{{q}^{\mathrm{2}} \left({p}−{R}\mathrm{cos}\:\theta\right)}{{p}^{\mathrm{2}} \left({q}−{R}\mathrm{sin}\:\theta\right)} \\ $$$$\Rightarrow\:\:{p}^{\mathrm{2}} {q}\mathrm{cos}\:\theta−{p}^{\mathrm{2}} {R}\mathrm{sin}\:\theta\mathrm{cos}\:\theta \\ $$$$\:\:\:\:=\:{pq}^{\mathrm{2}} \mathrm{sin}\:\theta−{q}^{\mathrm{2}} {R}\mathrm{sin}\:\theta\mathrm{cos}\:\theta \\ $$$$\Rightarrow\:\:{pq}\left({p}\mathrm{cos}\:\theta−{q}\mathrm{sin}\:\theta\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=\:\left({p}^{\mathrm{2}} −{q}^{\mathrm{2}} \right){R}\mathrm{sin}\:\theta\mathrm{cos}\:\theta \\ $$$$\:\:\:\:{R}=\frac{{pq}}{\left({p}^{\mathrm{2}} −{q}^{\mathrm{2}} \right)}\left(\frac{{p}}{\mathrm{sin}\:\theta}−\frac{{q}}{\mathrm{cos}\:\theta}\right) \\ $$$${s}^{\mathrm{2}} =\left({p}−{p}\mathrm{cos}\:\phi−{R}\right)^{\mathrm{2}} +\left({q}−{q}\mathrm{sin}\:\phi−{R}\right)^{\mathrm{2}} \\ $$$$\frac{{ds}^{\mathrm{2}} }{{d}\phi}=\mathrm{0}\:\:\Rightarrow \\ $$$${p}\left({p}−{p}\mathrm{cos}\:\phi−{R}\right)\mathrm{sin}\:\phi={q}\left({q}−{q}\mathrm{sin}\:\phi−{R}\right)\mathrm{cos}\:\phi \\ $$$$\Rightarrow\:\frac{{q}−{q}\mathrm{sin}\:\phi−{R}}{{p}−{p}\mathrm{cos}\:\phi−{R}}=\frac{{p}\mathrm{sin}\:\phi}{{q}\mathrm{cos}\:\phi} \\ $$$$\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_ \\ $$$${R}\left({p}\mathrm{sin}\:\phi−{q}\mathrm{cos}\:\phi\right)=\left({p}^{\mathrm{2}} −{q}^{\mathrm{2}} \right)\mathrm{sin}\:\phi\mathrm{cos}\:\phi \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\left({p}^{\mathrm{2}} \mathrm{sin}\:\phi−{q}^{\mathrm{2}} \mathrm{cos}\:\phi\right) \\ $$$${R}^{\mathrm{2}} =\left({p}−{p}\mathrm{cos}\:\phi−{R}\right)^{\mathrm{2}} +\left({q}−{q}\mathrm{sin}\:\phi−{R}\right)^{\mathrm{2}} \\ $$$$\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_ \\ $$$$ \\ $$
Answered by mr W last updated on 30/Dec/20
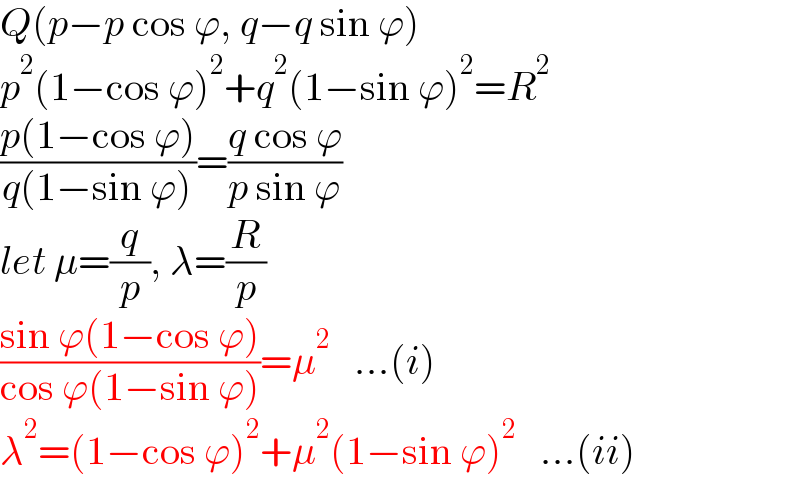
$${Q}\left({p}−{p}\:\mathrm{cos}\:\varphi,\:{q}−{q}\:\mathrm{sin}\:\varphi\right) \\ $$$${p}^{\mathrm{2}} \left(\mathrm{1}−\mathrm{cos}\:\varphi\right)^{\mathrm{2}} +{q}^{\mathrm{2}} \left(\mathrm{1}−\mathrm{sin}\:\varphi\right)^{\mathrm{2}} ={R}^{\mathrm{2}} \\ $$$$\frac{{p}\left(\mathrm{1}−\mathrm{cos}\:\varphi\right)}{{q}\left(\mathrm{1}−\mathrm{sin}\:\varphi\right)}=\frac{{q}\:\mathrm{cos}\:\varphi}{{p}\:\mathrm{sin}\:\varphi} \\ $$$${let}\:\mu=\frac{{q}}{{p}},\:\lambda=\frac{{R}}{{p}} \\ $$$$\frac{\mathrm{sin}\:\varphi\left(\mathrm{1}−\mathrm{cos}\:\varphi\right)}{\mathrm{cos}\:\varphi\left(\mathrm{1}−\mathrm{sin}\:\varphi\right)}=\mu^{\mathrm{2}} \:\:\:…\left({i}\right) \\ $$$$\lambda^{\mathrm{2}} =\left(\mathrm{1}−\mathrm{cos}\:\varphi\right)^{\mathrm{2}} +\mu^{\mathrm{2}} \left(\mathrm{1}−\mathrm{sin}\:\varphi\right)^{\mathrm{2}} \:\:\:…\left({ii}\right) \\ $$
Commented by mr W last updated on 30/Dec/20
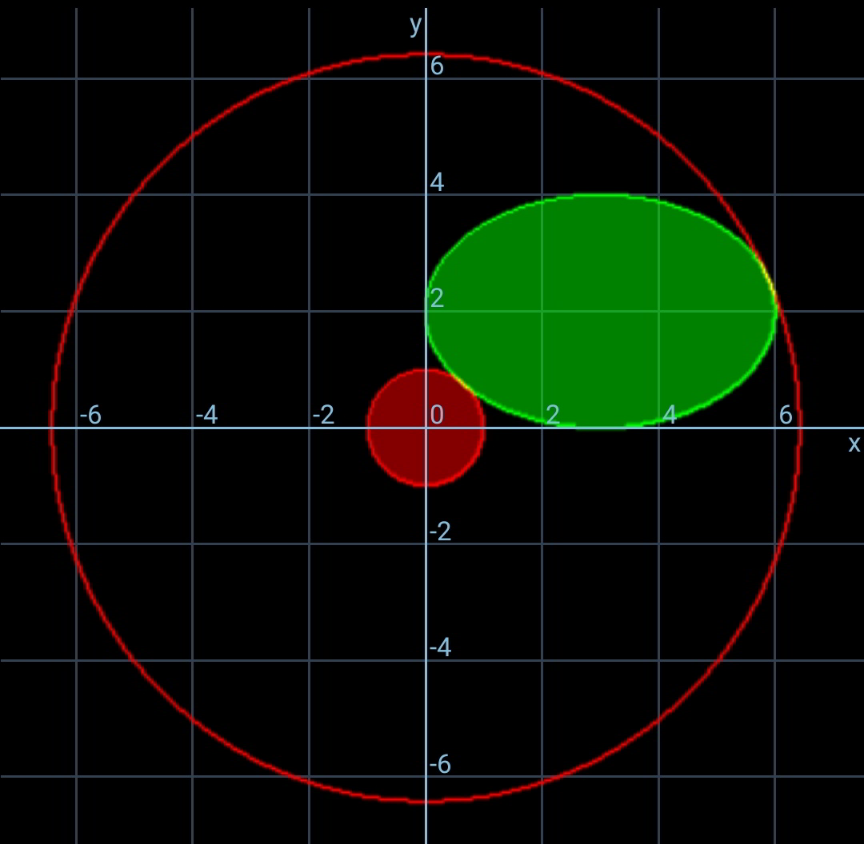
Commented by mr W last updated on 30/Dec/20
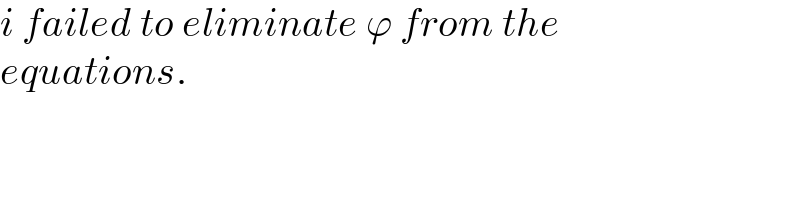
$${i}\:{failed}\:{to}\:{eliminate}\:\varphi\:{from}\:{the} \\ $$$${equations}. \\ $$
