Question Number 127481 by Mathgreat last updated on 30/Dec/20
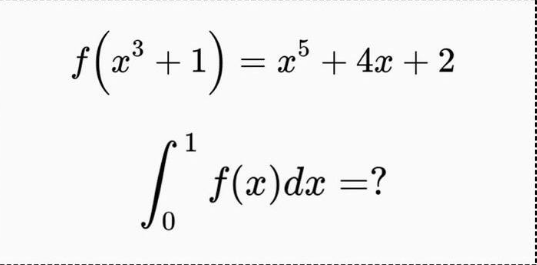
Commented by hknkrc46 last updated on 30/Dec/20
![g(x) = x^3 + 1 ⇒ g^(−1) (x) = ((x − 1))^(1/3) f(x^3 + 1)∣_((x − 1))^(1/3) = (x^5 + 4x + 2)∣_((x − 1))^(1/3) f(x) = (x − 1)^(5/3) + 4(x − 1)^(1/3) + 2 ∫_0 ^1 f(x)dx = ∫_(0) ^(1) [(x − 1)^(5/3) + 4(x − 1)^(1/3) + 2] = [(3/8)(x − 1)^(8/3) + 3(x − 1)^(4/3) + 2x]_0 ^1 = 2 − ((3/8) + 3) = −1 − (3/8) = −((11)/8)](https://www.tinkutara.com/question/Q127506.png)
$${g}\left({x}\right)\:=\:{x}^{\mathrm{3}} \:+\:\mathrm{1}\:\Rightarrow\:{g}^{−\mathrm{1}} \left({x}\right)\:=\:\sqrt[{\mathrm{3}}]{{x}\:−\:\mathrm{1}} \\ $$$${f}\left({x}^{\mathrm{3}} \:+\:\mathrm{1}\right)\mid_{\sqrt[{\mathrm{3}}]{{x}\:−\:\mathrm{1}}} \:=\:\left({x}^{\mathrm{5}} \:+\:\mathrm{4}{x}\:+\:\mathrm{2}\right)\mid_{\sqrt[{\mathrm{3}}]{{x}\:−\:\mathrm{1}}} \\ $$$${f}\left({x}\right)\:=\:\left({x}\:−\:\mathrm{1}\right)^{\frac{\mathrm{5}}{\mathrm{3}}} \:+\:\mathrm{4}\left({x}\:−\:\mathrm{1}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} \:+\:\mathrm{2} \\ $$$$\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\:{f}\left({x}\right){dx}\:=\:\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\:\left[\left({x}\:−\:\mathrm{1}\right)^{\frac{\mathrm{5}}{\mathrm{3}}} \:+\:\mathrm{4}\left({x}\:−\:\mathrm{1}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} \:+\:\mathrm{2}\right] \\ $$$$=\:\left[\frac{\mathrm{3}}{\mathrm{8}}\left({x}\:−\:\mathrm{1}\right)^{\frac{\mathrm{8}}{\mathrm{3}}} \:+\:\mathrm{3}\left({x}\:−\:\mathrm{1}\right)^{\frac{\mathrm{4}}{\mathrm{3}}} \:+\:\mathrm{2}{x}\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$=\:\mathrm{2}\:−\:\left(\frac{\mathrm{3}}{\mathrm{8}}\:+\:\mathrm{3}\right)\:=\:−\mathrm{1}\:−\:\frac{\mathrm{3}}{\mathrm{8}}\:=\:−\frac{\mathrm{11}}{\mathrm{8}} \\ $$
Answered by Olaf last updated on 30/Dec/20
![Ω = ∫_0 ^1 f(x)dx Let x = u^3 +1 Ω = ∫_(−1) ^0 f(u^3 +1)(3u^2 du) Ω = 3∫_(−1) ^0 (u^5 +4u+2)u^2 du Ω = 3[(x^8 /8)+x^4 +(2/3)x^3 ]_(−1) ^0 Ω = −3[(1/8)+1−(2/3)] Ω = −3×((11)/(24)) = −((11)/8)](https://www.tinkutara.com/question/Q127487.png)
$$\Omega\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} {f}\left({x}\right){dx} \\ $$$$\mathrm{Let}\:{x}\:=\:{u}^{\mathrm{3}} +\mathrm{1} \\ $$$$\Omega\:=\:\int_{−\mathrm{1}} ^{\mathrm{0}} {f}\left({u}^{\mathrm{3}} +\mathrm{1}\right)\left(\mathrm{3}{u}^{\mathrm{2}} {du}\right) \\ $$$$\Omega\:=\:\mathrm{3}\int_{−\mathrm{1}} ^{\mathrm{0}} \left({u}^{\mathrm{5}} +\mathrm{4}{u}+\mathrm{2}\right){u}^{\mathrm{2}} {du} \\ $$$$\Omega\:=\:\mathrm{3}\left[\frac{{x}^{\mathrm{8}} }{\mathrm{8}}+{x}^{\mathrm{4}} +\frac{\mathrm{2}}{\mathrm{3}}{x}^{\mathrm{3}} \right]_{−\mathrm{1}} ^{\mathrm{0}} \\ $$$$\Omega\:=\:−\mathrm{3}\left[\frac{\mathrm{1}}{\mathrm{8}}+\mathrm{1}−\frac{\mathrm{2}}{\mathrm{3}}\right] \\ $$$$\Omega\:=\:−\mathrm{3}×\frac{\mathrm{11}}{\mathrm{24}}\:=\:−\frac{\mathrm{11}}{\mathrm{8}} \\ $$
Answered by mathmax by abdo last updated on 31/Dec/20
![x^3 +1 =t ⇒x^3 =t−1 ⇒x=(t−1)^(1/3) ⇒f(t)=x^5 +4x+2 =(t−1)^(5/3) +4(t−1)^(1/3) +2 ⇒∫_0 ^1 f(t)dt =∫_0 ^1 (t−1)^(5/3) +4∫_0 ^1 (t−1)^(1/3) dt +2∫_0 ^1 dt =(1/(1+(5/3)))[(t−1)^(1+(5/3)) ]_0 ^1 +4 [(1/(1+(1/3)))(t−1)^((1/3)+1) ]_0 ^1 +2[t]_0 ^1 =(3/8)[(t−1)^(8/3) ]_0 ^1 +4×(3/4)[(t−1)^(4/3) ]_0 ^1 +2 =(3/8){−(−1)^(8/3) }+3{−(−1)^(4/3) } +2](https://www.tinkutara.com/question/Q127586.png)
$$\mathrm{x}^{\mathrm{3}} \:+\mathrm{1}\:=\mathrm{t}\:\Rightarrow\mathrm{x}^{\mathrm{3}} \:=\mathrm{t}−\mathrm{1}\:\Rightarrow\mathrm{x}=\left(\mathrm{t}−\mathrm{1}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} \:\Rightarrow\mathrm{f}\left(\mathrm{t}\right)=\mathrm{x}^{\mathrm{5}} \:+\mathrm{4x}+\mathrm{2} \\ $$$$=\left(\mathrm{t}−\mathrm{1}\right)^{\frac{\mathrm{5}}{\mathrm{3}}} \:+\mathrm{4}\left(\mathrm{t}−\mathrm{1}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} \:+\mathrm{2}\:\Rightarrow\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{f}\left(\mathrm{t}\right)\mathrm{dt} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{t}−\mathrm{1}\right)^{\frac{\mathrm{5}}{\mathrm{3}}} \:+\mathrm{4}\int_{\mathrm{0}} ^{\mathrm{1}} \:\left(\mathrm{t}−\mathrm{1}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} \:\mathrm{dt}\:\:+\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{1}+\frac{\mathrm{5}}{\mathrm{3}}}\left[\left(\mathrm{t}−\mathrm{1}\right)^{\mathrm{1}+\frac{\mathrm{5}}{\mathrm{3}}} \right]_{\mathrm{0}} ^{\mathrm{1}} \:+\mathrm{4}\:\left[\frac{\mathrm{1}}{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{3}}}\left(\mathrm{t}−\mathrm{1}\right)^{\frac{\mathrm{1}}{\mathrm{3}}+\mathrm{1}} \right]_{\mathrm{0}} ^{\mathrm{1}} \:+\mathrm{2}\left[\mathrm{t}\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$=\frac{\mathrm{3}}{\mathrm{8}}\left[\left(\mathrm{t}−\mathrm{1}\right)^{\frac{\mathrm{8}}{\mathrm{3}}} \right]_{\mathrm{0}} ^{\mathrm{1}} \:+\mathrm{4}×\frac{\mathrm{3}}{\mathrm{4}}\left[\left(\mathrm{t}−\mathrm{1}\right)^{\frac{\mathrm{4}}{\mathrm{3}}} \right]_{\mathrm{0}} ^{\mathrm{1}} \:+\mathrm{2} \\ $$$$=\frac{\mathrm{3}}{\mathrm{8}}\left\{−\left(−\mathrm{1}\right)^{\frac{\mathrm{8}}{\mathrm{3}}} \right\}+\mathrm{3}\left\{−\left(−\mathrm{1}\right)^{\frac{\mathrm{4}}{\mathrm{3}}} \right\}\:+\mathrm{2} \\ $$
