Question Number 127525 by Mathgreat last updated on 30/Dec/20

Commented by Mathgreat last updated on 30/Dec/20
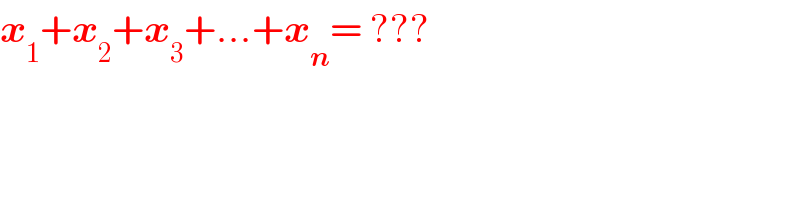
$$\boldsymbol{{x}}_{\mathrm{1}} +\boldsymbol{{x}}_{\mathrm{2}} +\boldsymbol{{x}}_{\mathrm{3}} +…+\boldsymbol{{x}}_{\boldsymbol{{n}}} =\:??? \\ $$
Commented by Mathgreat last updated on 30/Dec/20

$$\boldsymbol{{please}} \\ $$
Answered by MJS_new last updated on 31/Dec/20
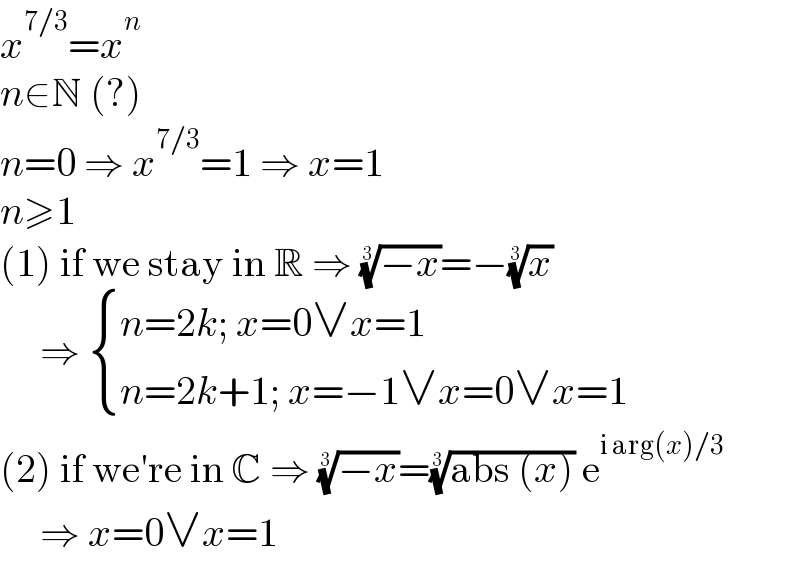
$${x}^{\mathrm{7}/\mathrm{3}} ={x}^{{n}} \\ $$$${n}\in\mathbb{N}\:\left(?\right) \\ $$$${n}=\mathrm{0}\:\Rightarrow\:{x}^{\mathrm{7}/\mathrm{3}} =\mathrm{1}\:\Rightarrow\:{x}=\mathrm{1} \\ $$$${n}\geqslant\mathrm{1} \\ $$$$\left(\mathrm{1}\right)\:\mathrm{if}\:\mathrm{we}\:\mathrm{stay}\:\mathrm{in}\:\mathbb{R}\:\Rightarrow\:\sqrt[{\mathrm{3}}]{−{x}}=−\sqrt[{\mathrm{3}}]{{x}} \\ $$$$\:\:\:\:\:\Rightarrow\:\begin{cases}{{n}=\mathrm{2}{k};\:{x}=\mathrm{0}\vee{x}=\mathrm{1}}\\{{n}=\mathrm{2}{k}+\mathrm{1};\:{x}=−\mathrm{1}\vee{x}=\mathrm{0}\vee{x}=\mathrm{1}}\end{cases} \\ $$$$\left(\mathrm{2}\right)\:\mathrm{if}\:\mathrm{we}'\mathrm{re}\:\mathrm{in}\:\mathbb{C}\:\Rightarrow\:\sqrt[{\mathrm{3}}]{−{x}}=\sqrt[{\mathrm{3}}]{\mathrm{abs}\:\left({x}\right)}\:\mathrm{e}^{\mathrm{i}\:\mathrm{arg}\left({x}\right)/\mathrm{3}} \\ $$$$\:\:\:\:\:\Rightarrow\:{x}=\mathrm{0}\vee{x}=\mathrm{1} \\ $$
