Question Number 127547 by Mathgreat last updated on 30/Dec/20

Answered by mr W last updated on 31/Dec/20

Commented by mr W last updated on 31/Dec/20
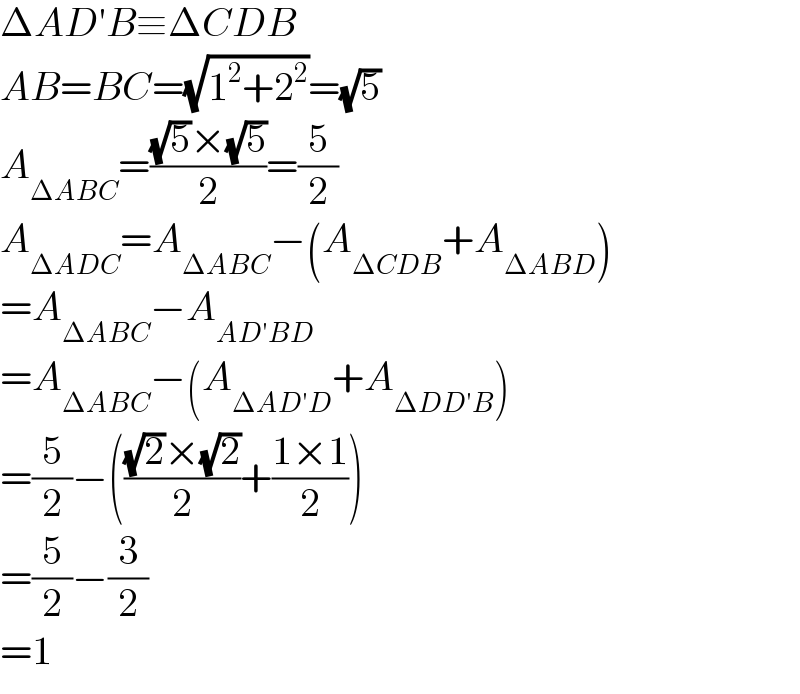
$$\Delta{AD}'{B}\equiv\Delta{CDB} \\ $$$${AB}={BC}=\sqrt{\mathrm{1}^{\mathrm{2}} +\mathrm{2}^{\mathrm{2}} }=\sqrt{\mathrm{5}} \\ $$$${A}_{\Delta{ABC}} =\frac{\sqrt{\mathrm{5}}×\sqrt{\mathrm{5}}}{\mathrm{2}}=\frac{\mathrm{5}}{\mathrm{2}} \\ $$$${A}_{\Delta{ADC}} ={A}_{\Delta{ABC}} −\left({A}_{\Delta{CDB}} +{A}_{\Delta{ABD}} \right) \\ $$$$={A}_{\Delta{ABC}} −{A}_{{AD}'{BD}} \\ $$$$={A}_{\Delta{ABC}} −\left({A}_{\Delta{AD}'{D}} +{A}_{\Delta{DD}'{B}} \right) \\ $$$$=\frac{\mathrm{5}}{\mathrm{2}}−\left(\frac{\sqrt{\mathrm{2}}×\sqrt{\mathrm{2}}}{\mathrm{2}}+\frac{\mathrm{1}×\mathrm{1}}{\mathrm{2}}\right) \\ $$$$=\frac{\mathrm{5}}{\mathrm{2}}−\frac{\mathrm{3}}{\mathrm{2}} \\ $$$$=\mathrm{1} \\ $$
Commented by mr W last updated on 31/Dec/20
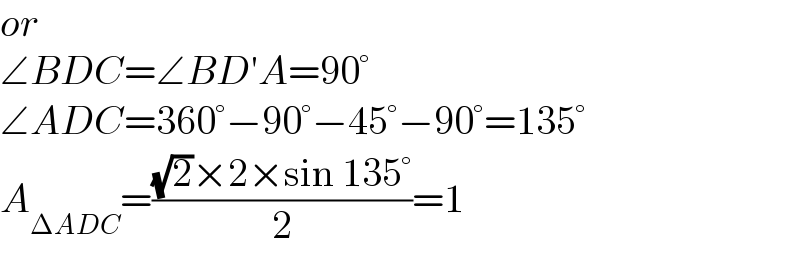
$${or} \\ $$$$\angle{BDC}=\angle{BD}'{A}=\mathrm{90}° \\ $$$$\angle{ADC}=\mathrm{360}°−\mathrm{90}°−\mathrm{45}°−\mathrm{90}°=\mathrm{135}° \\ $$$${A}_{\Delta{ADC}} =\frac{\sqrt{\mathrm{2}}×\mathrm{2}×\mathrm{sin}\:\mathrm{135}°}{\mathrm{2}}=\mathrm{1} \\ $$
