Question Number 127568 by Ar Brandon last updated on 30/Dec/20

Commented by bramlexs22 last updated on 30/Dec/20
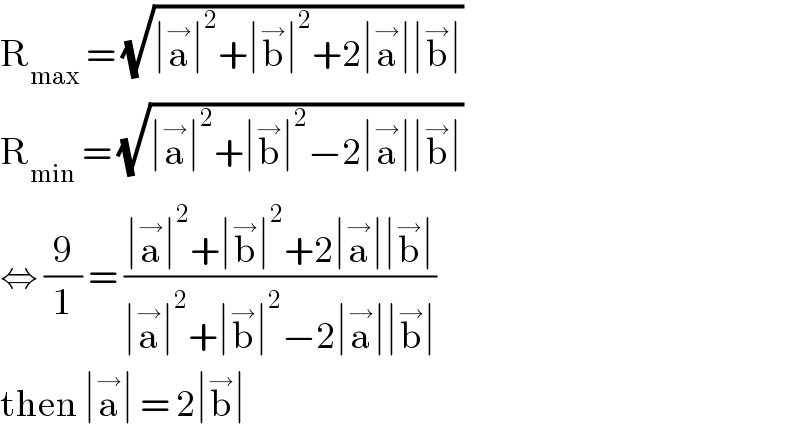
$$\mathrm{R}_{\mathrm{max}} \:=\:\sqrt{\mid\overset{\rightarrow} {\mathrm{a}}\mid^{\mathrm{2}} +\mid\overset{\rightarrow} {\mathrm{b}}\mid^{\mathrm{2}} +\mathrm{2}\mid\overset{\rightarrow} {\mathrm{a}}\mid\mid\overset{\rightarrow} {\mathrm{b}}\mid}\: \\ $$$$\mathrm{R}_{\mathrm{min}} \:=\:\sqrt{\mid\overset{\rightarrow} {\mathrm{a}}\mid^{\mathrm{2}} +\mid\overset{\rightarrow} {\mathrm{b}}\mid^{\mathrm{2}} −\mathrm{2}\mid\overset{\rightarrow} {\mathrm{a}}\mid\mid\overset{\rightarrow} {\mathrm{b}}\mid} \\ $$$$\Leftrightarrow\:\frac{\mathrm{9}}{\mathrm{1}}\:=\:\frac{\mid\overset{\rightarrow} {\mathrm{a}}\mid^{\mathrm{2}} +\mid\overset{\rightarrow} {\mathrm{b}}\mid^{\mathrm{2}} +\mathrm{2}\mid\overset{\rightarrow} {\mathrm{a}}\mid\mid\overset{\rightarrow} {\mathrm{b}}\mid}{\mid\overset{\rightarrow} {\mathrm{a}}\mid^{\mathrm{2}} +\mid\overset{\rightarrow} {\mathrm{b}}\mid^{\mathrm{2}} −\mathrm{2}\mid\overset{\rightarrow} {\mathrm{a}}\mid\mid\overset{\rightarrow} {\mathrm{b}}\mid} \\ $$$$\mathrm{then}\:\mid\overset{\rightarrow} {\mathrm{a}}\mid\:=\:\mathrm{2}\mid\overset{\rightarrow} {\mathrm{b}}\mid\: \\ $$
