Question Number 127633 by naka3546 last updated on 31/Dec/20

Commented by naka3546 last updated on 31/Dec/20

$${ABC}\:\:{is}\:\:{an}\:\:{equilateral}\:\:{triangle}\:. \\ $$$${Find}\:\:{area}\:\:{of}\:\:{ABC}\:! \\ $$
Commented by mr W last updated on 31/Dec/20
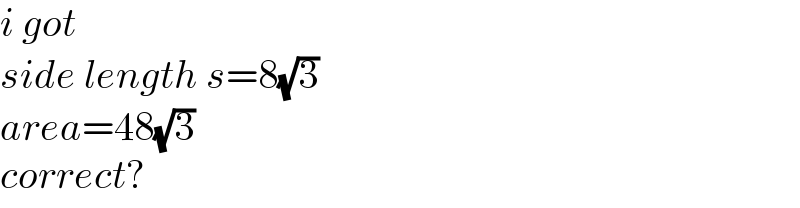
$${i}\:{got} \\ $$$${side}\:{length}\:{s}=\mathrm{8}\sqrt{\mathrm{3}} \\ $$$${area}=\mathrm{48}\sqrt{\mathrm{3}} \\ $$$${correct}? \\ $$
Commented by naka3546 last updated on 01/Jan/21

$${yes},\:{sir}.\:{Show}\:\:{your}\:\:{workings}\:,\:{please}\:. \\ $$
Commented by mr W last updated on 06/Jan/21
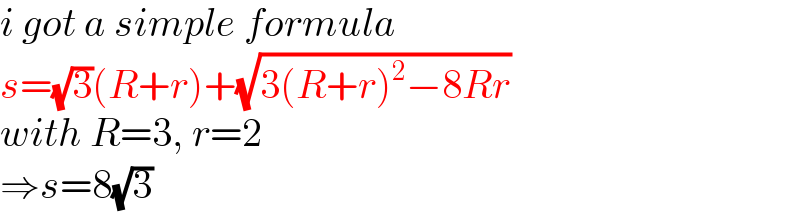
$${i}\:{got}\:{a}\:{simple}\:{formula}\: \\ $$$${s}=\sqrt{\mathrm{3}}\left({R}+{r}\right)+\sqrt{\mathrm{3}\left({R}+{r}\right)^{\mathrm{2}} −\mathrm{8}{Rr}} \\ $$$${with}\:{R}=\mathrm{3},\:{r}=\mathrm{2} \\ $$$$\Rightarrow{s}=\mathrm{8}\sqrt{\mathrm{3}} \\ $$
Answered by mr W last updated on 01/Jan/21

Commented by mr W last updated on 01/Jan/21

$$\boldsymbol{{METHOD}}\:\boldsymbol{{II}} \\ $$$${let}\:\angle{BDC}=\mathrm{2}\theta \\ $$$${BD}=\mathrm{3}\sqrt{\mathrm{3}}+\frac{\mathrm{3}}{\mathrm{tan}\:\theta} \\ $$$${AD}=\mathrm{2}\sqrt{\mathrm{3}}+\frac{\mathrm{2}}{\mathrm{tan}\:\left(\mathrm{90}−\theta\right)}=\mathrm{2}\sqrt{\mathrm{3}}+\mathrm{2}\:\mathrm{tan}\:\theta \\ $$$${AD}+{BD}={s}=\mathrm{5}\sqrt{\mathrm{3}}+\mathrm{2}\:\mathrm{tan}\:\theta+\frac{\mathrm{3}}{\mathrm{tan}\:\theta} \\ $$$$\frac{{BC}}{\mathrm{sin}\:\mathrm{2}\theta}=\frac{{BD}}{\mathrm{sin}\:\left(\mathrm{60}+\mathrm{2}\theta\right)} \\ $$$$\frac{\mathrm{sin}\:\left(\mathrm{60}+\mathrm{2}\theta\right)}{\mathrm{sin}\:\mathrm{2}\theta}=\frac{{BD}}{{BC}}=\frac{\mathrm{3}\left(\sqrt{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{tan}\:\theta}\right)}{{s}} \\ $$$$\frac{\sqrt{\mathrm{3}}}{\mathrm{2}\:\mathrm{tan}\:\mathrm{2}\theta}+\frac{\mathrm{1}}{\mathrm{2}}=\frac{\mathrm{3}\left(\sqrt{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{tan}\:\theta}\right)}{\mathrm{5}\sqrt{\mathrm{3}}+\mathrm{2}\:\mathrm{tan}\:\theta+\frac{\mathrm{3}}{\mathrm{tan}\:\theta}} \\ $$$$\frac{\sqrt{\mathrm{3}}}{\frac{\mathrm{2}\:\mathrm{tan}\:\theta}{\mathrm{1}−\mathrm{tan}^{\mathrm{2}} \:\theta}}+\mathrm{1}=\frac{\mathrm{6}\left(\sqrt{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{tan}\:\theta}\right)}{\mathrm{5}\sqrt{\mathrm{3}}+\mathrm{2}\:\mathrm{tan}\:\theta+\frac{\mathrm{3}}{\mathrm{tan}\:\theta}} \\ $$$${let}\:{t}=\mathrm{tan}\:\theta \\ $$$$\frac{\sqrt{\mathrm{3}}\left(\mathrm{1}−{t}^{\mathrm{2}} \right)+\mathrm{2}{t}}{\mathrm{2}{t}}=\frac{\mathrm{6}\left(\sqrt{\mathrm{3}}{t}+\mathrm{1}\right)}{\mathrm{5}\sqrt{\mathrm{3}}{t}+\mathrm{2}{t}^{\mathrm{2}} +\mathrm{3}} \\ $$$$\mathrm{2}\sqrt{\mathrm{3}}{t}^{\mathrm{4}} +\mathrm{11}{t}^{\mathrm{3}} +\mathrm{3}\sqrt{\mathrm{3}}{t}^{\mathrm{2}} −\mathrm{9}{t}−\mathrm{3}\sqrt{\mathrm{3}}=\mathrm{0} \\ $$$$\mathrm{6}\left(\frac{{t}}{\:\sqrt{\mathrm{3}}}\right)^{\mathrm{4}} +\mathrm{11}\left(\frac{{t}}{\:\sqrt{\mathrm{3}}}\right)^{\mathrm{3}} +\mathrm{3}\left(\frac{{t}}{\:\sqrt{\mathrm{3}}}\right)^{\mathrm{2}} −\mathrm{3}\left(\frac{{t}}{\:\sqrt{\mathrm{3}}}\right)−\mathrm{1}=\mathrm{0} \\ $$$$\left(\frac{{t}}{\:\sqrt{\mathrm{3}}}+\mathrm{1}\right)^{\mathrm{2}} \left(\frac{\mathrm{2}{t}}{\:\sqrt{\mathrm{3}}}−\mathrm{1}\right)\left(\frac{\mathrm{3}{t}}{\:\sqrt{\mathrm{3}}}+\mathrm{1}\right)=\mathrm{0} \\ $$$$\Rightarrow\frac{\mathrm{2}{t}}{\:\sqrt{\mathrm{3}}}−\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow{t}=\mathrm{tan}\:\theta=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$$\Rightarrow{s}=\mathrm{5}\sqrt{\mathrm{3}}+\mathrm{2}×\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}+\frac{\mathrm{3}}{\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}}=\mathrm{8}\sqrt{\mathrm{3}} \\ $$
Commented by naka3546 last updated on 01/Jan/21
$$\mathrm{ok},\:{sir}.\:{Thank}\:\:{you}\:\:{very}\:\:{much}\:. \\ $$
Commented by mr W last updated on 01/Jan/21
![METHOD I s=side length BL=BH=(3/(tan 30°))=3(√3) AK=AG=(2/(tan 30°))=2(√3) HC=s−3(√3) GC=s−2(√3) LK=s−3(√3)−2(√3)=s−5(√3) CF=(√(HC^2 +HF^2 ))=(√((s−3(√3))^2 +3^2 )) CE=(√(GC^2 +GE^2 ))=(√((s−2(√3))^2 +2^2 )) FE=(√(LK^2 +(LF−LE)^2 ))=(√((s−5(√3))^2 +(3−2)^2 )) ∠FCE=((60°)/2)=30° CE^2 +CF^2 −2×CE×CF×cos ∠FCE=FE^2 (s−2(√3))^2 +2^2 +(s−3(√3))^2 +3^2 −2(√([(s−2(√3))^2 +2^2 ][(s−3(√3))^2 +3^2 ]))cos 30°=(3−2)^2 +(s−2(√3)−3(√3))^2 s^2 −4(√3)s+16+s^2 −6(√3)s+36−(√(3[s^2 −4(√3)s+16][s^2 −6(√3)s+36]))=1+s^2 −10(√3)s+75 s^2 −24=(√(3[s^2 −4(√3)s+16][s^2 −6(√3)s+36])) s^4 −48s^2 +576=3[s^2 −4(√3)s+16][s^2 −6(√3)s+36] s^4 −48s^2 +576=3s^4 −30(√3)s^3 +372s^2 −720(√3)s+1728 s^4 −15(√3)s^3 +210s^2 −360(√3)s+576=0 ((s/( (√3))))^4 −15((s/( (√3))))^3 +70((s/( (√3))))^2 −120((s/( (√3))))+64=0 ((s/( (√3)))−1)((s/( (√3)))−2)((s/( (√3)))−4)((s/( (√3)))−8)=0 since s must be >2(√3)+3(√3)=5(√3) ⇒(s/( (√3)))=8 ⇒s=8(√3) Δ_(ABC) =(((√3)s^2 )/4)=(((√3)×(8(√3))^2 )/4)=48(√3)](https://www.tinkutara.com/question/Q127700.png)
$$\boldsymbol{{METHOD}}\:\boldsymbol{{I}} \\ $$$${s}={side}\:{length} \\ $$$${BL}={BH}=\frac{\mathrm{3}}{\mathrm{tan}\:\mathrm{30}°}=\mathrm{3}\sqrt{\mathrm{3}} \\ $$$${AK}={AG}=\frac{\mathrm{2}}{\mathrm{tan}\:\mathrm{30}°}=\mathrm{2}\sqrt{\mathrm{3}} \\ $$$${HC}={s}−\mathrm{3}\sqrt{\mathrm{3}} \\ $$$${GC}={s}−\mathrm{2}\sqrt{\mathrm{3}} \\ $$$${LK}={s}−\mathrm{3}\sqrt{\mathrm{3}}−\mathrm{2}\sqrt{\mathrm{3}}={s}−\mathrm{5}\sqrt{\mathrm{3}} \\ $$$${CF}=\sqrt{{HC}^{\mathrm{2}} +{HF}^{\mathrm{2}} }=\sqrt{\left({s}−\mathrm{3}\sqrt{\mathrm{3}}\right)^{\mathrm{2}} +\mathrm{3}^{\mathrm{2}} } \\ $$$${CE}=\sqrt{{GC}^{\mathrm{2}} +{GE}^{\mathrm{2}} }=\sqrt{\left({s}−\mathrm{2}\sqrt{\mathrm{3}}\right)^{\mathrm{2}} +\mathrm{2}^{\mathrm{2}} } \\ $$$${FE}=\sqrt{{LK}^{\mathrm{2}} +\left({LF}−{LE}\right)^{\mathrm{2}} }=\sqrt{\left({s}−\mathrm{5}\sqrt{\mathrm{3}}\right)^{\mathrm{2}} +\left(\mathrm{3}−\mathrm{2}\right)^{\mathrm{2}} } \\ $$$$\angle{FCE}=\frac{\mathrm{60}°}{\mathrm{2}}=\mathrm{30}° \\ $$$${CE}^{\mathrm{2}} +{CF}^{\mathrm{2}} −\mathrm{2}×{CE}×{CF}×\mathrm{cos}\:\angle{FCE}={FE}^{\mathrm{2}} \\ $$$$\left({s}−\mathrm{2}\sqrt{\mathrm{3}}\right)^{\mathrm{2}} +\mathrm{2}^{\mathrm{2}} +\left({s}−\mathrm{3}\sqrt{\mathrm{3}}\right)^{\mathrm{2}} +\mathrm{3}^{\mathrm{2}} −\mathrm{2}\sqrt{\left[\left({s}−\mathrm{2}\sqrt{\mathrm{3}}\right)^{\mathrm{2}} +\mathrm{2}^{\mathrm{2}} \right]\left[\left({s}−\mathrm{3}\sqrt{\mathrm{3}}\right)^{\mathrm{2}} +\mathrm{3}^{\mathrm{2}} \right]}\mathrm{cos}\:\mathrm{30}°=\left(\mathrm{3}−\mathrm{2}\right)^{\mathrm{2}} +\left({s}−\mathrm{2}\sqrt{\mathrm{3}}−\mathrm{3}\sqrt{\mathrm{3}}\right)^{\mathrm{2}} \\ $$$${s}^{\mathrm{2}} −\mathrm{4}\sqrt{\mathrm{3}}{s}+\mathrm{16}+{s}^{\mathrm{2}} −\mathrm{6}\sqrt{\mathrm{3}}{s}+\mathrm{36}−\sqrt{\mathrm{3}\left[{s}^{\mathrm{2}} −\mathrm{4}\sqrt{\mathrm{3}}{s}+\mathrm{16}\right]\left[{s}^{\mathrm{2}} −\mathrm{6}\sqrt{\mathrm{3}}{s}+\mathrm{36}\right]}=\mathrm{1}+{s}^{\mathrm{2}} −\mathrm{10}\sqrt{\mathrm{3}}{s}+\mathrm{75} \\ $$$${s}^{\mathrm{2}} −\mathrm{24}=\sqrt{\mathrm{3}\left[{s}^{\mathrm{2}} −\mathrm{4}\sqrt{\mathrm{3}}{s}+\mathrm{16}\right]\left[{s}^{\mathrm{2}} −\mathrm{6}\sqrt{\mathrm{3}}{s}+\mathrm{36}\right]} \\ $$$${s}^{\mathrm{4}} −\mathrm{48}{s}^{\mathrm{2}} +\mathrm{576}=\mathrm{3}\left[{s}^{\mathrm{2}} −\mathrm{4}\sqrt{\mathrm{3}}{s}+\mathrm{16}\right]\left[{s}^{\mathrm{2}} −\mathrm{6}\sqrt{\mathrm{3}}{s}+\mathrm{36}\right] \\ $$$${s}^{\mathrm{4}} −\mathrm{48}{s}^{\mathrm{2}} +\mathrm{576}=\mathrm{3}{s}^{\mathrm{4}} −\mathrm{30}\sqrt{\mathrm{3}}{s}^{\mathrm{3}} +\mathrm{372}{s}^{\mathrm{2}} −\mathrm{720}\sqrt{\mathrm{3}}{s}+\mathrm{1728} \\ $$$${s}^{\mathrm{4}} −\mathrm{15}\sqrt{\mathrm{3}}{s}^{\mathrm{3}} +\mathrm{210}{s}^{\mathrm{2}} −\mathrm{360}\sqrt{\mathrm{3}}{s}+\mathrm{576}=\mathrm{0} \\ $$$$\left(\frac{{s}}{\:\sqrt{\mathrm{3}}}\right)^{\mathrm{4}} −\mathrm{15}\left(\frac{{s}}{\:\sqrt{\mathrm{3}}}\right)^{\mathrm{3}} +\mathrm{70}\left(\frac{{s}}{\:\sqrt{\mathrm{3}}}\right)^{\mathrm{2}} −\mathrm{120}\left(\frac{{s}}{\:\sqrt{\mathrm{3}}}\right)+\mathrm{64}=\mathrm{0} \\ $$$$\left(\frac{{s}}{\:\sqrt{\mathrm{3}}}−\mathrm{1}\right)\left(\frac{{s}}{\:\sqrt{\mathrm{3}}}−\mathrm{2}\right)\left(\frac{{s}}{\:\sqrt{\mathrm{3}}}−\mathrm{4}\right)\left(\frac{{s}}{\:\sqrt{\mathrm{3}}}−\mathrm{8}\right)=\mathrm{0} \\ $$$${since}\:{s}\:{must}\:{be}\:>\mathrm{2}\sqrt{\mathrm{3}}+\mathrm{3}\sqrt{\mathrm{3}}=\mathrm{5}\sqrt{\mathrm{3}} \\ $$$$\Rightarrow\frac{{s}}{\:\sqrt{\mathrm{3}}}=\mathrm{8} \\ $$$$\Rightarrow{s}=\mathrm{8}\sqrt{\mathrm{3}} \\ $$$$\Delta_{{ABC}} =\frac{\sqrt{\mathrm{3}}{s}^{\mathrm{2}} }{\mathrm{4}}=\frac{\sqrt{\mathrm{3}}×\left(\mathrm{8}\sqrt{\mathrm{3}}\right)^{\mathrm{2}} }{\mathrm{4}}=\mathrm{48}\sqrt{\mathrm{3}} \\ $$
Commented by behi83417@gmail.com last updated on 02/Jan/21
![BH=(3/(tg30))=3(√3)⇒F(3(√3),3) ⇒(x−3(√3))^2 +(y−3)^2 =9 CD:y=m(x−a) (x−3(√3))^2 +[m(x−a)−3]^2 =9 ⇒x^2 +27−6(√3)x+m^2 x^2 −2m^2 ax+m^2 a^2 + −6mx+6ma=0 ⇒(1+m^2 )x^2 −2(m^2 a+3(√3)+3m)x+ +m^2 a^2 +6ma+27=0 △′=(m^2 a+3(√3)+3m)^2 −(1+m^2 )(m^2 a^2 +6ma+27)= =m^4 a^2 +27+9m^2 +6(√3)m^2 a+6m^3 a+18(√3)m− −(m^2 a^2 +6ma+27+m^4 a^2 +6m^3 a+27m^2 )= =−18m^2 +6(√3)m^2 a+18(√3)m−6ma−m^2 a^2 =0 ⇒−m^2 (18−6(√3)a+a^2 )−6m(a−3(√3))=0 ⇒^(m≠0) { ((a−3(√3)=0⇒a=3(√3)[not ok])),((a^2 −6(√3)a+18=0⇒a=3((√3)+1))) :} sir:mrW! what is wrong?](https://www.tinkutara.com/question/Q127841.png)
$$\mathrm{BH}=\frac{\mathrm{3}}{\mathrm{tg30}}=\mathrm{3}\sqrt{\mathrm{3}}\Rightarrow\mathrm{F}\left(\mathrm{3}\sqrt{\mathrm{3}},\mathrm{3}\right) \\ $$$$\Rightarrow\left(\mathrm{x}−\mathrm{3}\sqrt{\mathrm{3}}\right)^{\mathrm{2}} +\left(\mathrm{y}−\mathrm{3}\right)^{\mathrm{2}} =\mathrm{9} \\ $$$$\mathrm{CD}:\mathrm{y}=\mathrm{m}\left(\mathrm{x}−\mathrm{a}\right) \\ $$$$\left(\mathrm{x}−\mathrm{3}\sqrt{\mathrm{3}}\right)^{\mathrm{2}} +\left[\mathrm{m}\left(\mathrm{x}−\mathrm{a}\right)−\mathrm{3}\right]^{\mathrm{2}} =\mathrm{9} \\ $$$$\Rightarrow\mathrm{x}^{\mathrm{2}} +\mathrm{27}−\mathrm{6}\sqrt{\mathrm{3}}\mathrm{x}+\mathrm{m}^{\mathrm{2}} \mathrm{x}^{\mathrm{2}} −\mathrm{2m}^{\mathrm{2}} \mathrm{ax}+\mathrm{m}^{\mathrm{2}} \mathrm{a}^{\mathrm{2}} + \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\mathrm{6mx}+\mathrm{6ma}=\mathrm{0} \\ $$$$\Rightarrow\left(\mathrm{1}+\mathrm{m}^{\mathrm{2}} \right)\mathrm{x}^{\mathrm{2}} −\mathrm{2}\left(\mathrm{m}^{\mathrm{2}} \mathrm{a}+\mathrm{3}\sqrt{\mathrm{3}}+\mathrm{3m}\right)\mathrm{x}+ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:+\mathrm{m}^{\mathrm{2}} \mathrm{a}^{\mathrm{2}} +\mathrm{6ma}+\mathrm{27}=\mathrm{0} \\ $$$$\bigtriangleup'=\left(\mathrm{m}^{\mathrm{2}} \mathrm{a}+\mathrm{3}\sqrt{\mathrm{3}}+\mathrm{3m}\right)^{\mathrm{2}} −\left(\mathrm{1}+\mathrm{m}^{\mathrm{2}} \right)\left(\mathrm{m}^{\mathrm{2}} \mathrm{a}^{\mathrm{2}} +\mathrm{6ma}+\mathrm{27}\right)= \\ $$$$=\mathrm{m}^{\mathrm{4}} \mathrm{a}^{\mathrm{2}} +\mathrm{27}+\mathrm{9m}^{\mathrm{2}} +\mathrm{6}\sqrt{\mathrm{3}}\mathrm{m}^{\mathrm{2}} \mathrm{a}+\mathrm{6m}^{\mathrm{3}} \mathrm{a}+\mathrm{18}\sqrt{\mathrm{3}}\mathrm{m}− \\ $$$$−\left(\mathrm{m}^{\mathrm{2}} \mathrm{a}^{\mathrm{2}} +\mathrm{6ma}+\mathrm{27}+\mathrm{m}^{\mathrm{4}} \mathrm{a}^{\mathrm{2}} +\mathrm{6m}^{\mathrm{3}} \mathrm{a}+\mathrm{27m}^{\mathrm{2}} \right)= \\ $$$$=−\mathrm{18m}^{\mathrm{2}} +\mathrm{6}\sqrt{\mathrm{3}}\mathrm{m}^{\mathrm{2}} \mathrm{a}+\mathrm{18}\sqrt{\mathrm{3}}\mathrm{m}−\mathrm{6ma}−\mathrm{m}^{\mathrm{2}} \mathrm{a}^{\mathrm{2}} =\mathrm{0} \\ $$$$\Rightarrow−\mathrm{m}^{\mathrm{2}} \left(\mathrm{18}−\mathrm{6}\sqrt{\mathrm{3}}\mathrm{a}+\mathrm{a}^{\mathrm{2}} \right)−\mathrm{6m}\left(\mathrm{a}−\mathrm{3}\sqrt{\mathrm{3}}\right)=\mathrm{0} \\ $$$$\overset{\mathrm{m}\neq\mathrm{0}} {\Rightarrow}\begin{cases}{\mathrm{a}−\mathrm{3}\sqrt{\mathrm{3}}=\mathrm{0}\Rightarrow\mathrm{a}=\mathrm{3}\sqrt{\mathrm{3}}\left[\mathrm{not}\:\mathrm{ok}\right]}\\{\mathrm{a}^{\mathrm{2}} −\mathrm{6}\sqrt{\mathrm{3}}\mathrm{a}+\mathrm{18}=\mathrm{0}\Rightarrow\mathrm{a}=\mathrm{3}\left(\sqrt{\mathrm{3}}+\mathrm{1}\right)}\end{cases} \\ $$$$\mathrm{sir}:\mathrm{mrW}!\:\mathrm{what}\:\mathrm{is}\:\mathrm{wrong}? \\ $$$$\:\:\:\: \\ $$
Commented by mr W last updated on 02/Jan/21
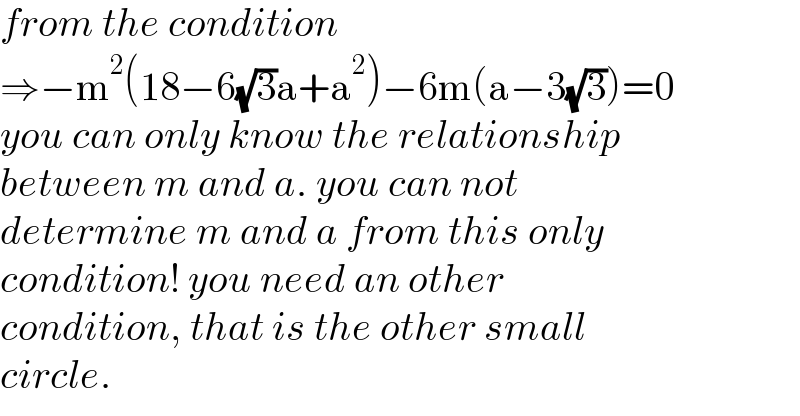
$${from}\:{the}\:{condition} \\ $$$$\Rightarrow−\mathrm{m}^{\mathrm{2}} \left(\mathrm{18}−\mathrm{6}\sqrt{\mathrm{3}}\mathrm{a}+\mathrm{a}^{\mathrm{2}} \right)−\mathrm{6m}\left(\mathrm{a}−\mathrm{3}\sqrt{\mathrm{3}}\right)=\mathrm{0} \\ $$$${you}\:{can}\:{only}\:{know}\:{the}\:{relationship} \\ $$$${between}\:{m}\:{and}\:{a}.\:{you}\:{can}\:{not}\: \\ $$$${determine}\:{m}\:{and}\:{a}\:{from}\:{this}\:{only} \\ $$$${condition}!\:{you}\:{need}\:{an}\:{other}\: \\ $$$${condition},\:{that}\:{is}\:{the}\:{other}\:{small} \\ $$$${circle}. \\ $$
Answered by behi83417@gmail.com last updated on 02/Jan/21
![s_1 =p_1 .r_1 =((x+a+z)/2).2,AB=a,AD=x,CD=z s_2 =p_2 .r_2 =((y+a+z)/2).3,BD=y s=((a^2 (√3))/4)=((2(x+a+z)+3(y+a+z))/2)= =((7a+5z+y)/2)⇒a^2 (√3)=2(7a+5z+y) a.(z^2 +xy)=a^2 .x+a^2 .y=a^2 (x+y)=a^3 ⇒ { ((a^2 (√3)=2(7a+5z+y))),((z^2 +xy=a^2 ⇒z^2 +(a−y)y=a^2 )) :} ⇒ { ((a^2 (√3)−2(7a+y)=10z)),((z^2 =a^2 −ay+y^2 )) :} ⇒[a^2 (√3)−2(7a+y)]^2 =100(a^2 −ay+y^2 ) ⇒3a^4 −4a^2 (√3)(7a+y)+4(7a+y)^2 = =100a^2 −100ay+100y^2 ⇒3a^4 −28a^3 (√3)−4a^2 y(√3)+196a^2 +56ay+4y^2 = =100a^2 −100ay+100y^2 ⇒96y^2 −156ay+4a^2 y(√3)+28a^3 (√3)−3a^4 −96a^2 =0 ⇒96y^2 −2a(78−2a(√3))y−a^2 (3a^2 −28a(√3)+96)=0 △′=a^2 .(78−2a(√3))^2 +96a^2 (3a^2 −28a(√3)+96)= =a^2 [6084−312a(√3)+12a^2 +288a^2 −2688a(√3)+9216]= =a^2 [300a^2 −3000a(√3)+15300]= =300a^2 [a^2 −10a(√3)+51] ⇒y=((a(39−a(√3))±5a(√3).(√(a^2 −10a(√3)+51)))/(48))](https://www.tinkutara.com/question/Q127822.png)
$$\mathrm{s}_{\mathrm{1}} =\mathrm{p}_{\mathrm{1}} .\mathrm{r}_{\mathrm{1}} =\frac{\mathrm{x}+\mathrm{a}+\mathrm{z}}{\mathrm{2}}.\mathrm{2},\mathrm{AB}=\mathrm{a},\mathrm{AD}=\mathrm{x},\mathrm{CD}=\mathrm{z} \\ $$$$\mathrm{s}_{\mathrm{2}} =\mathrm{p}_{\mathrm{2}} .\mathrm{r}_{\mathrm{2}} =\frac{\mathrm{y}+\mathrm{a}+\mathrm{z}}{\mathrm{2}}.\mathrm{3},\mathrm{BD}=\mathrm{y} \\ $$$$\mathrm{s}=\frac{\mathrm{a}^{\mathrm{2}} \sqrt{\mathrm{3}}}{\mathrm{4}}=\frac{\mathrm{2}\left(\mathrm{x}+\mathrm{a}+\mathrm{z}\right)+\mathrm{3}\left(\mathrm{y}+\mathrm{a}+\mathrm{z}\right)}{\mathrm{2}}= \\ $$$$=\frac{\mathrm{7a}+\mathrm{5z}+\mathrm{y}}{\mathrm{2}}\Rightarrow\mathrm{a}^{\mathrm{2}} \sqrt{\mathrm{3}}=\mathrm{2}\left(\mathrm{7a}+\mathrm{5z}+\mathrm{y}\right) \\ $$$$\mathrm{a}.\left(\mathrm{z}^{\mathrm{2}} +\mathrm{xy}\right)=\mathrm{a}^{\mathrm{2}} .\mathrm{x}+\mathrm{a}^{\mathrm{2}} .\mathrm{y}=\mathrm{a}^{\mathrm{2}} \left(\mathrm{x}+\mathrm{y}\right)=\mathrm{a}^{\mathrm{3}} \\ $$$$\Rightarrow\begin{cases}{\mathrm{a}^{\mathrm{2}} \sqrt{\mathrm{3}}=\mathrm{2}\left(\mathrm{7a}+\mathrm{5z}+\mathrm{y}\right)}\\{\mathrm{z}^{\mathrm{2}} +\mathrm{xy}=\mathrm{a}^{\mathrm{2}} \Rightarrow\mathrm{z}^{\mathrm{2}} +\left(\mathrm{a}−\mathrm{y}\right)\mathrm{y}=\mathrm{a}^{\mathrm{2}} }\end{cases} \\ $$$$\Rightarrow\begin{cases}{\mathrm{a}^{\mathrm{2}} \sqrt{\mathrm{3}}−\mathrm{2}\left(\mathrm{7a}+\mathrm{y}\right)=\mathrm{10z}}\\{\mathrm{z}^{\mathrm{2}} =\mathrm{a}^{\mathrm{2}} −\mathrm{ay}+\mathrm{y}^{\mathrm{2}} }\end{cases} \\ $$$$\Rightarrow\left[\mathrm{a}^{\mathrm{2}} \sqrt{\mathrm{3}}−\mathrm{2}\left(\mathrm{7a}+\mathrm{y}\right)\right]^{\mathrm{2}} =\mathrm{100}\left(\mathrm{a}^{\mathrm{2}} −\mathrm{ay}+\mathrm{y}^{\mathrm{2}} \right) \\ $$$$\Rightarrow\mathrm{3a}^{\mathrm{4}} −\mathrm{4a}^{\mathrm{2}} \sqrt{\mathrm{3}}\left(\mathrm{7a}+\mathrm{y}\right)+\mathrm{4}\left(\mathrm{7a}+\mathrm{y}\right)^{\mathrm{2}} = \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{100a}^{\mathrm{2}} −\mathrm{100ay}+\mathrm{100y}^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{3a}^{\mathrm{4}} −\mathrm{28a}^{\mathrm{3}} \sqrt{\mathrm{3}}−\mathrm{4a}^{\mathrm{2}} \mathrm{y}\sqrt{\mathrm{3}}+\mathrm{196a}^{\mathrm{2}} +\mathrm{56ay}+\mathrm{4y}^{\mathrm{2}} = \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\mathrm{100a}^{\mathrm{2}} −\mathrm{100ay}+\mathrm{100y}^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{96y}^{\mathrm{2}} −\mathrm{156ay}+\mathrm{4a}^{\mathrm{2}} \mathrm{y}\sqrt{\mathrm{3}}+\mathrm{28a}^{\mathrm{3}} \sqrt{\mathrm{3}}−\mathrm{3a}^{\mathrm{4}} −\mathrm{96a}^{\mathrm{2}} =\mathrm{0} \\ $$$$\Rightarrow\mathrm{96y}^{\mathrm{2}} −\mathrm{2a}\left(\mathrm{78}−\mathrm{2a}\sqrt{\mathrm{3}}\right)\mathrm{y}−\mathrm{a}^{\mathrm{2}} \left(\mathrm{3a}^{\mathrm{2}} −\mathrm{28a}\sqrt{\mathrm{3}}+\mathrm{96}\right)=\mathrm{0} \\ $$$$\bigtriangleup'=\mathrm{a}^{\mathrm{2}} .\left(\mathrm{78}−\mathrm{2a}\sqrt{\mathrm{3}}\right)^{\mathrm{2}} +\mathrm{96a}^{\mathrm{2}} \left(\mathrm{3a}^{\mathrm{2}} −\mathrm{28a}\sqrt{\mathrm{3}}+\mathrm{96}\right)= \\ $$$$=\mathrm{a}^{\mathrm{2}} \left[\mathrm{6084}−\mathrm{312a}\sqrt{\mathrm{3}}+\mathrm{12a}^{\mathrm{2}} +\mathrm{288a}^{\mathrm{2}} −\mathrm{2688a}\sqrt{\mathrm{3}}+\mathrm{9216}\right]= \\ $$$$=\mathrm{a}^{\mathrm{2}} \left[\mathrm{300a}^{\mathrm{2}} −\mathrm{3000a}\sqrt{\mathrm{3}}+\mathrm{15300}\right]= \\ $$$$=\mathrm{300a}^{\mathrm{2}} \left[\mathrm{a}^{\mathrm{2}} −\mathrm{10a}\sqrt{\mathrm{3}}+\mathrm{51}\right] \\ $$$$\Rightarrow\mathrm{y}=\frac{\mathrm{a}\left(\mathrm{39}−\mathrm{a}\sqrt{\mathrm{3}}\right)\pm\mathrm{5a}\sqrt{\mathrm{3}}.\sqrt{\mathrm{a}^{\mathrm{2}} −\mathrm{10a}\sqrt{\mathrm{3}}+\mathrm{51}}}{\mathrm{48}} \\ $$
Commented by behi83417@gmail.com last updated on 02/Jan/21
$$\mathrm{sir}:\mathrm{mrW}!\:\mathrm{what}\:\mathrm{is}\:\mathrm{wrong}\:\mathrm{there}? \\ $$
Commented by behi83417@gmail.com last updated on 02/Jan/21

$$\mathrm{thanks}\:\mathrm{a}\:\mathrm{lot}\:\mathrm{for}\:\mathrm{your}\:\mathrm{time}\:\mathrm{mr}.\mathrm{proph}. \\ $$
Commented by mr W last updated on 02/Jan/21

$${i}\:{can}'{t}\:{follow}\:{your}\:{idea}.\:{since}\:{you} \\ $$$${didn}'{t}\:{come}\:{to}\:{a}\:{final}\:{result},\:{i}\:{can}'{t} \\ $$$${say}\:{if}\:{it}'{s}\:{correct}\:{or}\:{not}. \\ $$
