Question Number 127781 by shaker last updated on 02/Jan/21

Answered by bemath last updated on 02/Jan/21
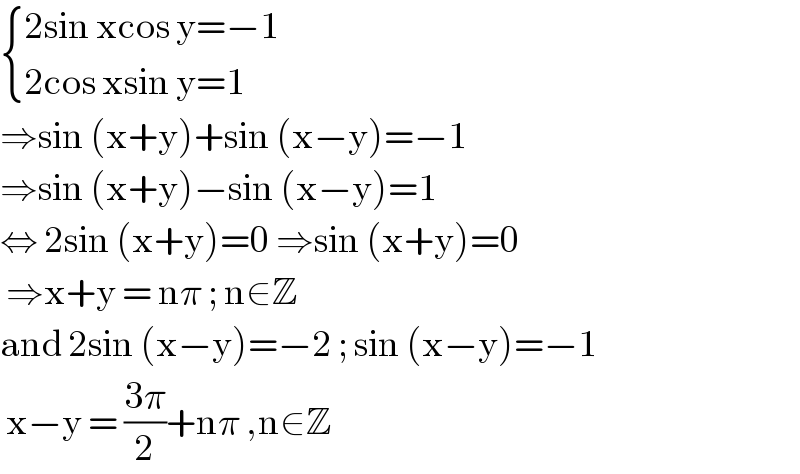
$$\begin{cases}{\mathrm{2sin}\:\mathrm{xcos}\:\mathrm{y}=−\mathrm{1}}\\{\mathrm{2cos}\:\mathrm{xsin}\:\mathrm{y}=\mathrm{1}}\end{cases} \\ $$$$\Rightarrow\mathrm{sin}\:\left(\mathrm{x}+\mathrm{y}\right)+\mathrm{sin}\:\left(\mathrm{x}−\mathrm{y}\right)=−\mathrm{1} \\ $$$$\Rightarrow\mathrm{sin}\:\left(\mathrm{x}+\mathrm{y}\right)−\mathrm{sin}\:\left(\mathrm{x}−\mathrm{y}\right)=\mathrm{1} \\ $$$$\Leftrightarrow\:\mathrm{2sin}\:\left(\mathrm{x}+\mathrm{y}\right)=\mathrm{0}\:\Rightarrow\mathrm{sin}\:\left(\mathrm{x}+\mathrm{y}\right)=\mathrm{0} \\ $$$$\:\Rightarrow\mathrm{x}+\mathrm{y}\:=\:\mathrm{n}\pi\:;\:\mathrm{n}\in\mathbb{Z}\: \\ $$$$\mathrm{and}\:\mathrm{2sin}\:\left(\mathrm{x}−\mathrm{y}\right)=−\mathrm{2}\:;\:\mathrm{sin}\:\left(\mathrm{x}−\mathrm{y}\right)=−\mathrm{1} \\ $$$$\:\mathrm{x}−\mathrm{y}\:=\:\frac{\mathrm{3}\pi}{\mathrm{2}}+\mathrm{n}\pi\:,\mathrm{n}\in\mathbb{Z} \\ $$
