Question Number 127952 by rs4089 last updated on 03/Jan/21
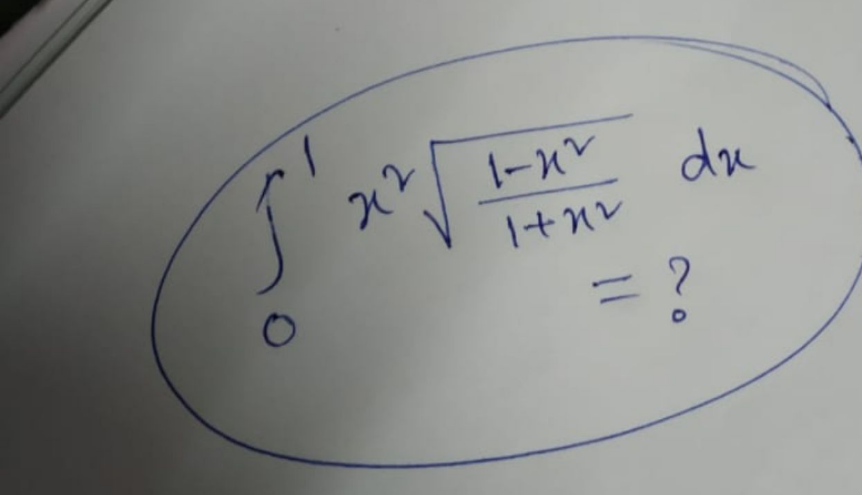
Answered by Ar Brandon last updated on 03/Jan/21
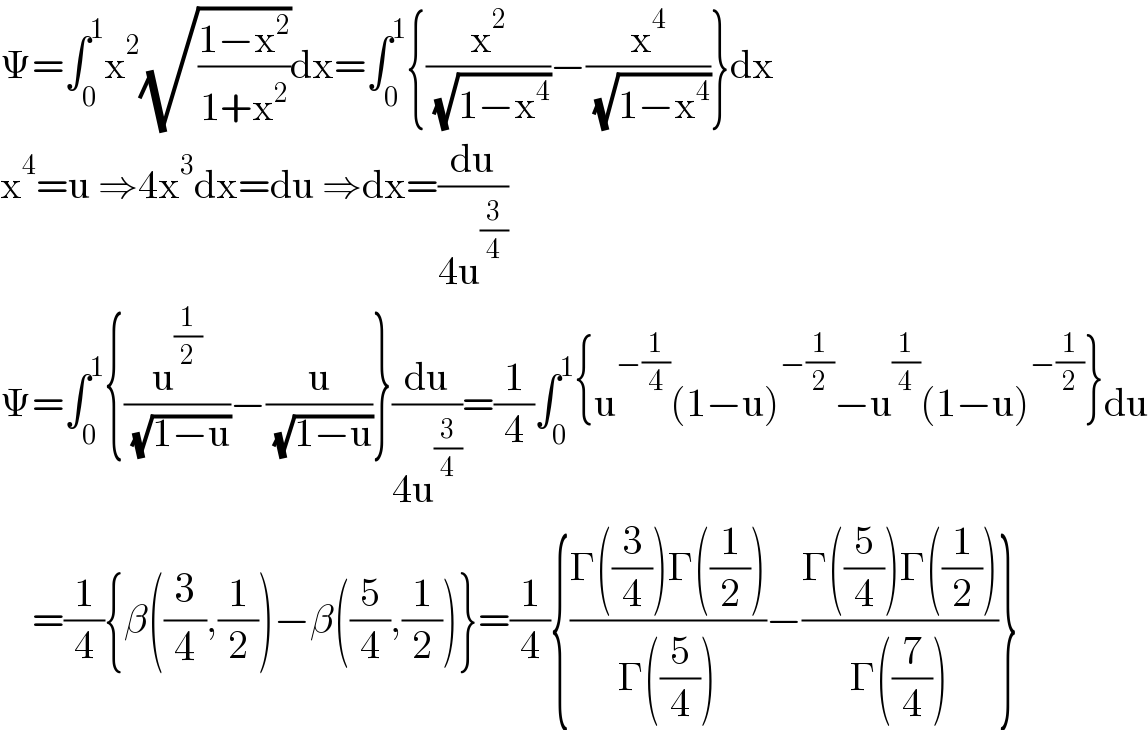
$$\Psi=\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{x}^{\mathrm{2}} \sqrt{\frac{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }}\mathrm{dx}=\int_{\mathrm{0}} ^{\mathrm{1}} \left\{\frac{\mathrm{x}^{\mathrm{2}} }{\:\sqrt{\mathrm{1}−\mathrm{x}^{\mathrm{4}} }}−\frac{\mathrm{x}^{\mathrm{4}} }{\:\sqrt{\mathrm{1}−\mathrm{x}^{\mathrm{4}} }}\right\}\mathrm{dx} \\ $$$$\mathrm{x}^{\mathrm{4}} =\mathrm{u}\:\Rightarrow\mathrm{4x}^{\mathrm{3}} \mathrm{dx}=\mathrm{du}\:\Rightarrow\mathrm{dx}=\frac{\mathrm{du}}{\mathrm{4u}^{\frac{\mathrm{3}}{\mathrm{4}}} } \\ $$$$\Psi=\int_{\mathrm{0}} ^{\mathrm{1}} \left\{\frac{\mathrm{u}^{\frac{\mathrm{1}}{\mathrm{2}}} }{\:\sqrt{\mathrm{1}−\mathrm{u}}}−\frac{\mathrm{u}}{\:\sqrt{\mathrm{1}−\mathrm{u}}}\right\}\frac{\mathrm{du}}{\mathrm{4u}^{\frac{\mathrm{3}}{\mathrm{4}}} }=\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{\mathrm{1}} \left\{\mathrm{u}^{−\frac{\mathrm{1}}{\mathrm{4}}} \left(\mathrm{1}−\mathrm{u}\right)^{−\frac{\mathrm{1}}{\mathrm{2}}} −\mathrm{u}^{\frac{\mathrm{1}}{\mathrm{4}}} \left(\mathrm{1}−\mathrm{u}\right)^{−\frac{\mathrm{1}}{\mathrm{2}}} \right\}\mathrm{du} \\ $$$$\:\:\:\:=\frac{\mathrm{1}}{\mathrm{4}}\left\{\beta\left(\frac{\mathrm{3}}{\mathrm{4}},\frac{\mathrm{1}}{\mathrm{2}}\right)−\beta\left(\frac{\mathrm{5}}{\mathrm{4}},\frac{\mathrm{1}}{\mathrm{2}}\right)\right\}=\frac{\mathrm{1}}{\mathrm{4}}\left\{\frac{\Gamma\left(\frac{\mathrm{3}}{\mathrm{4}}\right)\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right)}{\Gamma\left(\frac{\mathrm{5}}{\mathrm{4}}\right)}−\frac{\Gamma\left(\frac{\mathrm{5}}{\mathrm{4}}\right)\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right)}{\Gamma\left(\frac{\mathrm{7}}{\mathrm{4}}\right)}\right\} \\ $$
Commented by Ar Brandon last updated on 03/Jan/21
![=(1/4){(((√π)Γ((3/4)))/((1/4)Γ((1/4))))−(((√π)(1/4)Γ((1/4)))/((3/4)Γ((3/4))))}=(√π)[((3Γ^2 ((3/4))−(1/4)Γ^2 ((1/4)))/(3Γ((1/4))Γ((3/4))))] =(√π)[((3Γ^2 ((3/4))−(1/4)Γ^2 ((1/4)))/(3(π/(sin((π/4))))))]=(1/(3(√(2π))))[3Γ^2 ((3/4))−(1/4)Γ^2 ((1/4))]](https://www.tinkutara.com/question/Q127972.png)
$$\:\:\:\:=\frac{\mathrm{1}}{\mathrm{4}}\left\{\frac{\sqrt{\pi}\Gamma\left(\frac{\mathrm{3}}{\mathrm{4}}\right)}{\frac{\mathrm{1}}{\mathrm{4}}\Gamma\left(\frac{\mathrm{1}}{\mathrm{4}}\right)}−\frac{\sqrt{\pi}\frac{\mathrm{1}}{\mathrm{4}}\Gamma\left(\frac{\mathrm{1}}{\mathrm{4}}\right)}{\frac{\mathrm{3}}{\mathrm{4}}\Gamma\left(\frac{\mathrm{3}}{\mathrm{4}}\right)}\right\}=\sqrt{\pi}\left[\frac{\mathrm{3}\Gamma^{\mathrm{2}} \left(\frac{\mathrm{3}}{\mathrm{4}}\right)−\frac{\mathrm{1}}{\mathrm{4}}\Gamma^{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{4}}\right)}{\mathrm{3}\Gamma\left(\frac{\mathrm{1}}{\mathrm{4}}\right)\Gamma\left(\frac{\mathrm{3}}{\mathrm{4}}\right)}\right] \\ $$$$\:\:\:\:=\sqrt{\pi}\left[\frac{\mathrm{3}\Gamma^{\mathrm{2}} \left(\frac{\mathrm{3}}{\mathrm{4}}\right)−\frac{\mathrm{1}}{\mathrm{4}}\Gamma^{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{4}}\right)}{\mathrm{3}\frac{\pi}{\mathrm{sin}\left(\frac{\pi}{\mathrm{4}}\right)}}\right]=\frac{\mathrm{1}}{\mathrm{3}\sqrt{\mathrm{2}\pi}}\left[\mathrm{3}\Gamma^{\mathrm{2}} \left(\frac{\mathrm{3}}{\mathrm{4}}\right)−\frac{\mathrm{1}}{\mathrm{4}}\Gamma^{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{4}}\right)\right] \\ $$
