Question Number 128025 by Algoritm last updated on 03/Jan/21
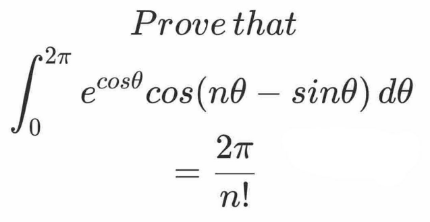
Answered by Olaf last updated on 03/Jan/21
![Let Φ_n = ∫_0 ^(2π) e^(cosθ) cos(nθ−sinθ)dθ Let Ω_n = ∫_0 ^(2π) e^(cosθ) e^(i(nθ−sinθ)) dθ Ω_n = ∫_0 ^(2π) e^e^(−iθ) e^(inθ) dθ Ω_n = i∫_0 ^(2π) (−ie^(−iθ) e^e^(−iθ) )e^(i(n+1)θ) dθ Ω_n = i[e^e^(−iθ) e^(i(n+1)θ) ]_0 ^(2π) −i∫_0 ^(2π) e^e^(−iθ) i(n+1)e^(i(n+1)θ) dθ Ω_n = (n+1)Ω_(n+1) Ω_(n+1) = (Ω_n /(n+1)) (1) Ω_0 = ∫_0 ^(2π) e^e^(−iθ) dθ Ω_0 = ∫_C e^z^− dz (C : trigonometric circle) Ω_0 = ∫_C e^z dz = 2πr (with r = 1) Ω_0 = 2π (2) (1) and (2) : Ω_n = ((2π)/(n!)) (real number) Φ_n = Re(Ω_n ) = Ω_n = ((2π)/(n!))](https://www.tinkutara.com/question/Q128027.png)
$$\mathrm{Let}\:\Phi_{{n}} \:=\:\int_{\mathrm{0}} ^{\mathrm{2}\pi} {e}^{\mathrm{cos}\theta} \mathrm{cos}\left({n}\theta−\mathrm{sin}\theta\right){d}\theta \\ $$$$\mathrm{Let}\:\Omega_{{n}} \:=\:\int_{\mathrm{0}} ^{\mathrm{2}\pi} {e}^{\mathrm{cos}\theta} {e}^{{i}\left({n}\theta−\mathrm{sin}\theta\right)} {d}\theta \\ $$$$\Omega_{{n}} \:=\:\int_{\mathrm{0}} ^{\mathrm{2}\pi} {e}^{{e}^{−{i}\theta} } {e}^{{in}\theta} {d}\theta \\ $$$$\Omega_{{n}} \:=\:{i}\int_{\mathrm{0}} ^{\mathrm{2}\pi} \left(−{ie}^{−{i}\theta} {e}^{{e}^{−{i}\theta} } \right){e}^{{i}\left({n}+\mathrm{1}\right)\theta} {d}\theta \\ $$$$\Omega_{{n}} \:=\:{i}\left[{e}^{{e}^{−{i}\theta} } {e}^{{i}\left({n}+\mathrm{1}\right)\theta} \right]_{\mathrm{0}} ^{\mathrm{2}\pi} −{i}\int_{\mathrm{0}} ^{\mathrm{2}\pi} {e}^{{e}^{−{i}\theta} } {i}\left({n}+\mathrm{1}\right){e}^{{i}\left({n}+\mathrm{1}\right)\theta} {d}\theta \\ $$$$\Omega_{{n}} \:=\:\left({n}+\mathrm{1}\right)\Omega_{{n}+\mathrm{1}} \\ $$$$\Omega_{{n}+\mathrm{1}} \:=\:\frac{\Omega_{{n}} }{{n}+\mathrm{1}}\:\left(\mathrm{1}\right) \\ $$$$\Omega_{\mathrm{0}} \:=\:\int_{\mathrm{0}} ^{\mathrm{2}\pi} {e}^{{e}^{−{i}\theta} } {d}\theta \\ $$$$\Omega_{\mathrm{0}} \:=\:\int_{\mathcal{C}} {e}^{\overset{−} {{z}}} {dz}\:\left(\mathcal{C}\::\:\mathrm{trigonometric}\:\mathrm{circle}\right) \\ $$$$\Omega_{\mathrm{0}} \:=\:\int_{\mathcal{C}} {e}^{{z}} {dz}\:=\:\mathrm{2}\pi{r}\:\left(\mathrm{with}\:{r}\:=\:\mathrm{1}\right) \\ $$$$\Omega_{\mathrm{0}} \:=\:\mathrm{2}\pi\:\left(\mathrm{2}\right) \\ $$$$\left(\mathrm{1}\right)\:\mathrm{and}\:\left(\mathrm{2}\right)\::\:\Omega_{{n}} \:=\:\frac{\mathrm{2}\pi}{{n}!}\:\left(\mathrm{real}\:\mathrm{number}\right) \\ $$$$\Phi_{{n}} \:=\:\mathrm{Re}\left(\Omega_{{n}} \right)\:=\:\Omega_{{n}} \:=\:\frac{\mathrm{2}\pi}{{n}!} \\ $$
Commented by mindispower last updated on 03/Jan/21

$${nice}\:{way}\:{sir}\: \\ $$
Answered by mindispower last updated on 03/Jan/21
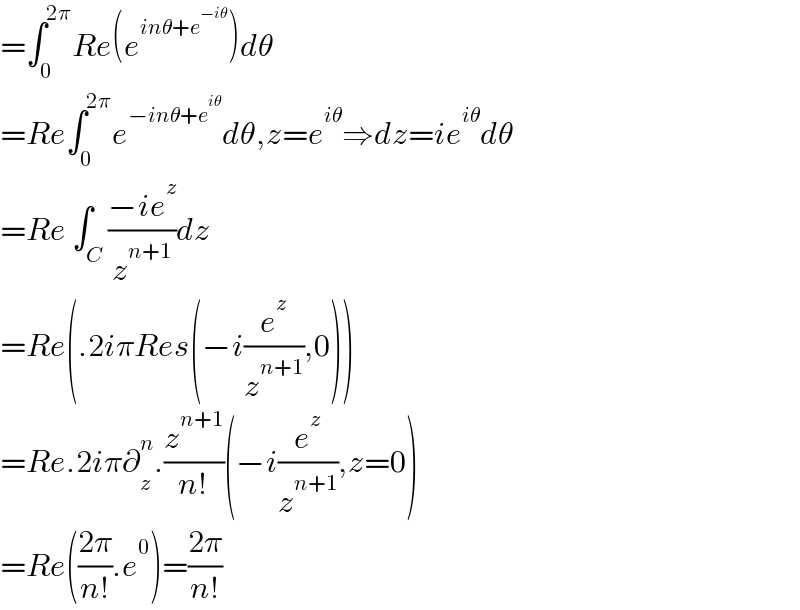
$$=\int_{\mathrm{0}} ^{\mathrm{2}\pi} {Re}\left({e}^{{in}\theta+{e}^{−{i}\theta} } \right){d}\theta\: \\ $$$$={Re}\int_{\mathrm{0}} ^{\mathrm{2}\pi} {e}^{−{in}\theta+{e}^{{i}\theta} } {d}\theta,{z}={e}^{{i}\theta} \Rightarrow{dz}={ie}^{{i}\theta} {d}\theta \\ $$$$={Re}\:\int_{{C}} \frac{−{ie}^{{z}} }{{z}^{{n}+\mathrm{1}} }{dz} \\ $$$$={Re}\left(.\mathrm{2}{i}\pi{Res}\left(−{i}\frac{{e}^{{z}} }{{z}^{{n}+\mathrm{1}} },\mathrm{0}\right)\right) \\ $$$$={Re}.\mathrm{2}{i}\pi\partial_{{z}} ^{{n}} .\frac{{z}^{{n}+\mathrm{1}} }{{n}!}\left(−{i}\frac{{e}^{{z}} }{{z}^{{n}+\mathrm{1}} },{z}=\mathrm{0}\right) \\ $$$$={Re}\left(\frac{\mathrm{2}\pi}{{n}!}.{e}^{\mathrm{0}} \right)=\frac{\mathrm{2}\pi}{{n}!} \\ $$
