Question Number 128069 by 0731619177 last updated on 04/Jan/21
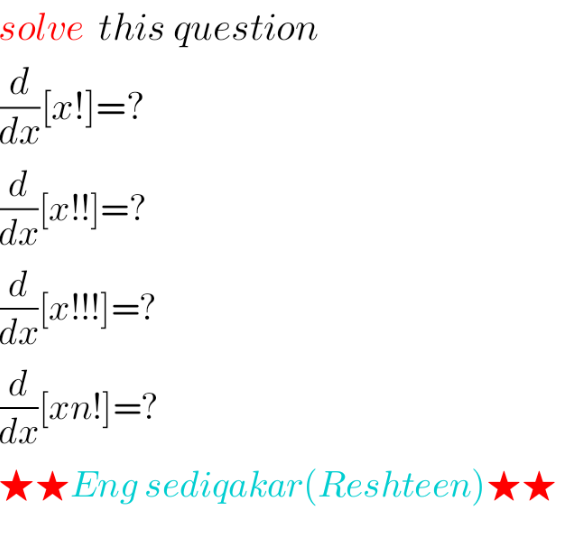
Answered by Dwaipayan Shikari last updated on 04/Jan/21
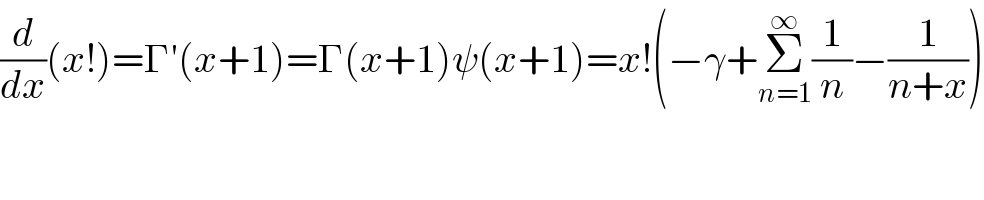
$$\frac{{d}}{{dx}}\left({x}!\right)=\Gamma'\left({x}+\mathrm{1}\right)=\Gamma\left({x}+\mathrm{1}\right)\psi\left({x}+\mathrm{1}\right)={x}!\left(−\gamma+\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}}−\frac{\mathrm{1}}{{n}+{x}}\right) \\ $$
Answered by A8;15: last updated on 04/Jan/21
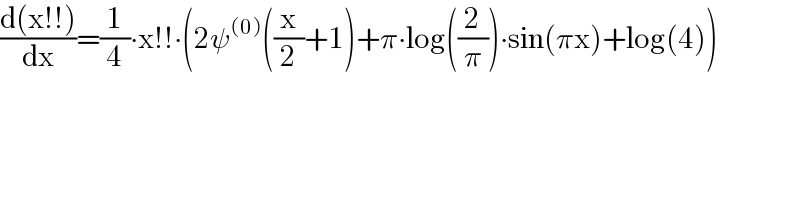
$$\frac{\mathrm{d}\left(\mathrm{x}!!\right)}{\mathrm{dx}}=\frac{\mathrm{1}}{\mathrm{4}}\centerdot\mathrm{x}!!\centerdot\left(\mathrm{2}\psi^{\left(\mathrm{0}\right)} \left(\frac{\mathrm{x}}{\mathrm{2}}+\mathrm{1}\right)+\pi\centerdot\mathrm{log}\left(\frac{\mathrm{2}}{\pi}\right)\centerdot\mathrm{sin}\left(\pi\mathrm{x}\right)+\mathrm{log}\left(\mathrm{4}\right)\right) \\ $$
