Question Number 128093 by BHOOPENDRA last updated on 04/Jan/21

Answered by Dwaipayan Shikari last updated on 04/Jan/21
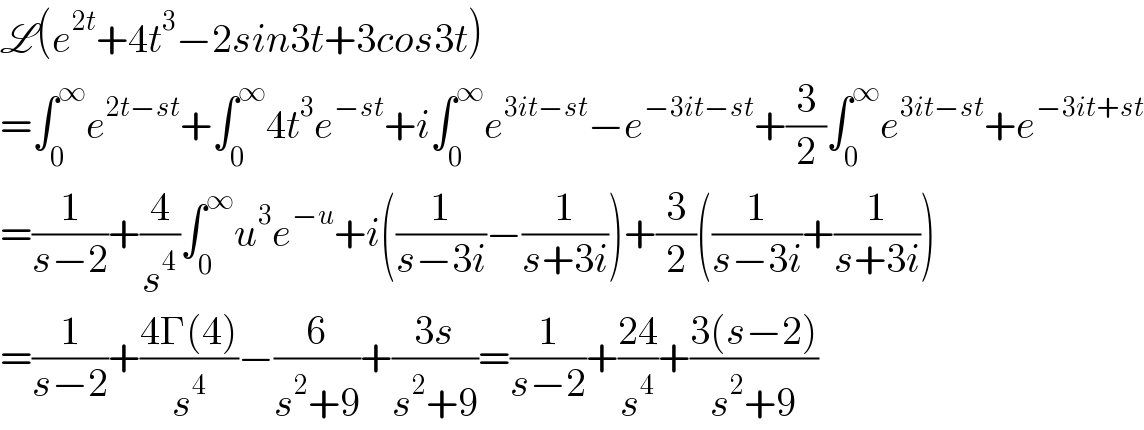
$$\mathscr{L}\left({e}^{\mathrm{2}{t}} +\mathrm{4}{t}^{\mathrm{3}} −\mathrm{2}{sin}\mathrm{3}{t}+\mathrm{3}{cos}\mathrm{3}{t}\right) \\ $$$$=\int_{\mathrm{0}} ^{\infty} {e}^{\mathrm{2}{t}−{st}} +\int_{\mathrm{0}} ^{\infty} \mathrm{4}{t}^{\mathrm{3}} {e}^{−{st}} +{i}\int_{\mathrm{0}} ^{\infty} {e}^{\mathrm{3}{it}−{st}} −{e}^{−\mathrm{3}{it}−{st}} +\frac{\mathrm{3}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} {e}^{\mathrm{3}{it}−{st}} +{e}^{−\mathrm{3}{it}+{st}} \\ $$$$=\frac{\mathrm{1}}{{s}−\mathrm{2}}+\frac{\mathrm{4}}{{s}^{\mathrm{4}} }\int_{\mathrm{0}} ^{\infty} {u}^{\mathrm{3}} {e}^{−{u}} +{i}\left(\frac{\mathrm{1}}{{s}−\mathrm{3}{i}}−\frac{\mathrm{1}}{{s}+\mathrm{3}{i}}\right)+\frac{\mathrm{3}}{\mathrm{2}}\left(\frac{\mathrm{1}}{{s}−\mathrm{3}{i}}+\frac{\mathrm{1}}{{s}+\mathrm{3}{i}}\right) \\ $$$$=\frac{\mathrm{1}}{{s}−\mathrm{2}}+\frac{\mathrm{4}\Gamma\left(\mathrm{4}\right)}{{s}^{\mathrm{4}} }−\frac{\mathrm{6}}{{s}^{\mathrm{2}} +\mathrm{9}}+\frac{\mathrm{3}{s}}{{s}^{\mathrm{2}} +\mathrm{9}}=\frac{\mathrm{1}}{{s}−\mathrm{2}}+\frac{\mathrm{24}}{{s}^{\mathrm{4}} }+\frac{\mathrm{3}\left({s}−\mathrm{2}\right)}{{s}^{\mathrm{2}} +\mathrm{9}} \\ $$
Commented by BHOOPENDRA last updated on 04/Jan/21

$${thankyou} \\ $$
