Question Number 128181 by Algoritm last updated on 05/Jan/21
Commented by Algoritm last updated on 05/Jan/21

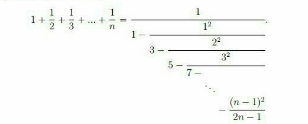
$$\mathrm{Prove}\:\mathrm{that} \\ $$
Answered by Dwaipayan Shikari last updated on 05/Jan/21
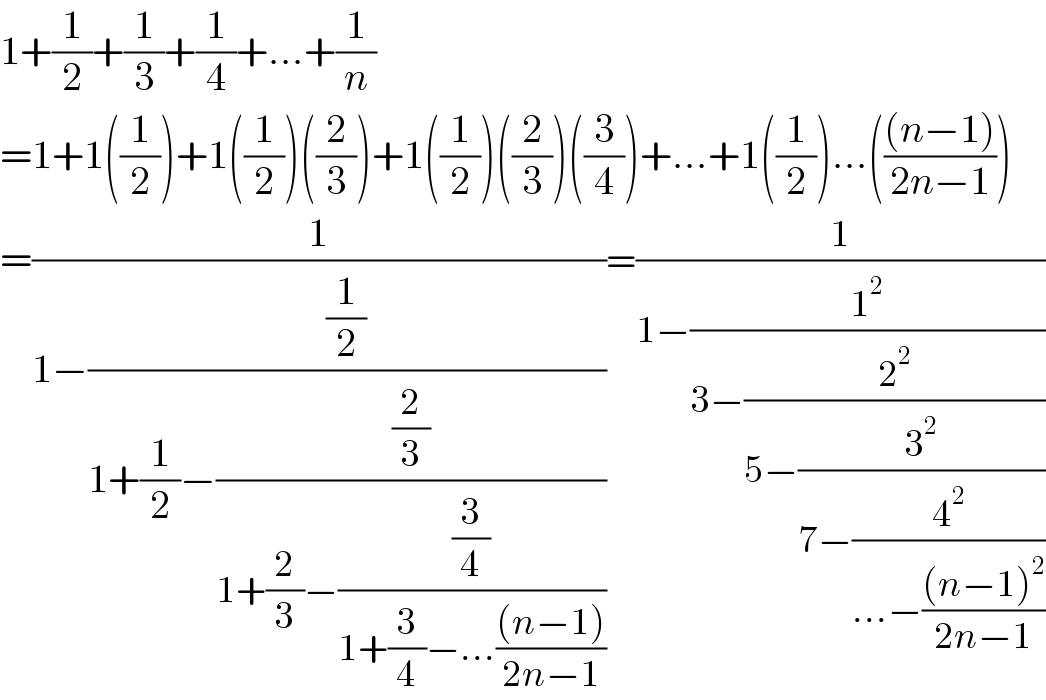
$$\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{4}}+…+\frac{\mathrm{1}}{{n}} \\ $$$$=\mathrm{1}+\mathrm{1}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)+\mathrm{1}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\left(\frac{\mathrm{2}}{\mathrm{3}}\right)+\mathrm{1}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\left(\frac{\mathrm{2}}{\mathrm{3}}\right)\left(\frac{\mathrm{3}}{\mathrm{4}}\right)+…+\mathrm{1}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)…\left(\frac{\left({n}−\mathrm{1}\right)}{\mathrm{2}{n}−\mathrm{1}}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{1}−\frac{\frac{\mathrm{1}}{\mathrm{2}}}{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}−\frac{\frac{\mathrm{2}}{\mathrm{3}}}{\mathrm{1}+\frac{\mathrm{2}}{\mathrm{3}}−\frac{\frac{\mathrm{3}}{\mathrm{4}}}{\mathrm{1}+\frac{\mathrm{3}}{\mathrm{4}}−…\frac{\left({n}−\mathrm{1}\right)}{\mathrm{2}{n}−\mathrm{1}}}}}}=\frac{\mathrm{1}}{\mathrm{1}−\frac{\mathrm{1}^{\mathrm{2}} }{\mathrm{3}−\frac{\mathrm{2}^{\mathrm{2}} }{\mathrm{5}−\frac{\mathrm{3}^{\mathrm{2}} }{\mathrm{7}−\frac{\mathrm{4}^{\mathrm{2}} }{…−\frac{\left({n}−\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{2}{n}−\mathrm{1}}}}}}} \\ $$
Commented by Dwaipayan Shikari last updated on 05/Jan/21
see Euler continued fractions
https://en.wikipedia.org/wiki/Euler%27s_continued_fraction_formula
